如何理解三大微分中值定理？（转）

今天看高数的微分中值定理，前两个中值定理到还是看的很简单，但是到了第三的柯西中值定理的时候，有了一些疑惑，我一直想研究它的几何意义，可惜课本并没有画出来，按照课本的意思柯西中值定理就是拉格朗日中值定理的参数方程形式，我头铁的想直接用两个拉格朗日中值定理的表达式凑出柯西中值定理表达式，结果却发现两个ξ可能不是同一个，后来发现了这样一篇文章，通过画图，利用一些物理现象来解释微分中值定理，尤其是哪个二维空间运动的图形用于解释柯西中值定理真的是太形象了。

---

 

微分中值定理是很重要的基础定理，很多定理都是以它为基础进行证明的。

1 罗尔中值定理

1.1 直觉

这是往返跑：

可以认为他从 点出发，经过一段时间又回到了 点，画成 （位移-时间）图就是：

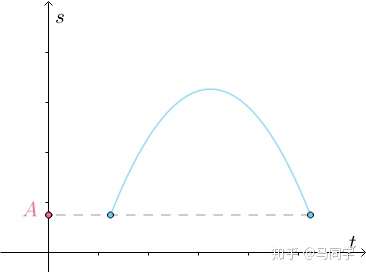
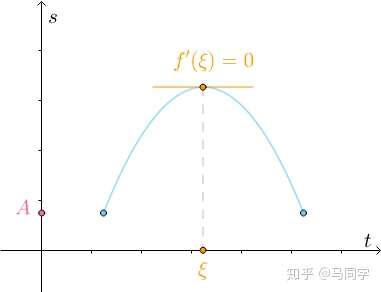
根据常识，因为要回到起点，中间必定有速度为0的点：

拳击比赛中，步伐复杂：

但不论怎样，只要最后回到起点，中间必定有速度为0的点：

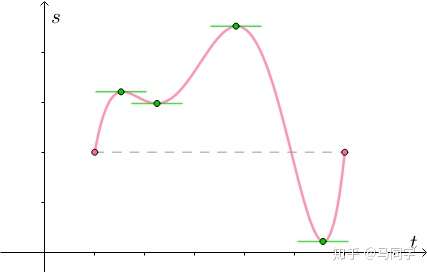
这就是罗尔中值定理。

1.2 罗尔中值定理

设函数满足以下三个条件：

• 在闭区间 上连续
• 在开区间 上可导
• 

则存在 ，使得

在闭区间 连续是必须的，否则有可能没有 ：

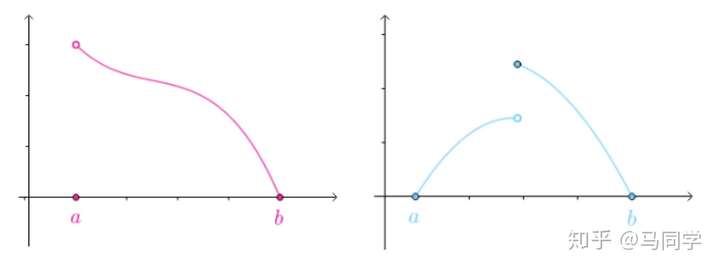
在开区间 可导也是必须的：

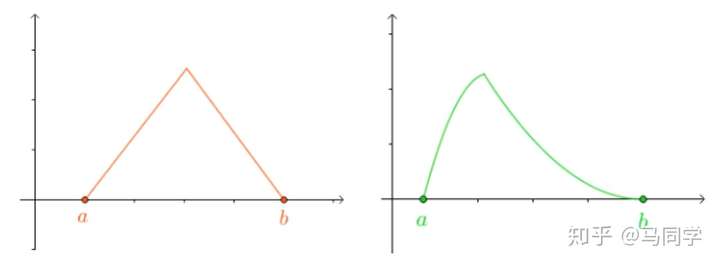
1.3 拓展

可能有的同学觉得，定理中的条件“ 在闭区间 连续、在 可导”比较古怪，为什么不是“ 在闭区间 连续、在 可导”？

大概有两个原因，首先，“开区间可导”条件更弱，包含了“闭区间可导”；其次，”开区间可导”的函数并不一定就“闭区间可导”，比如：

此函数在图像如下：

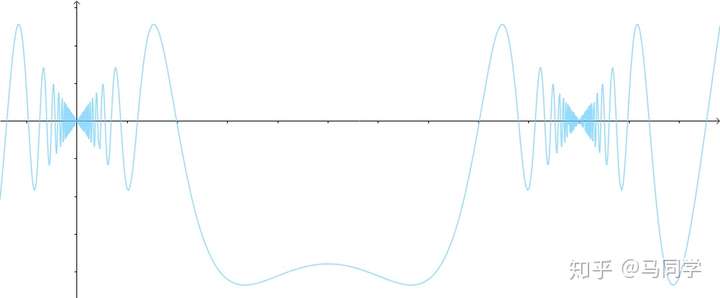
此函数就是在 连续， 可导，在端点 处导数不存在（类似于在0点处不可导，可自行证明）。

2 拉格朗日中值定理

来看下交通管理中的区间测速：

时间 采集到汽车的位移为 ，时间 采集到汽车的位移为

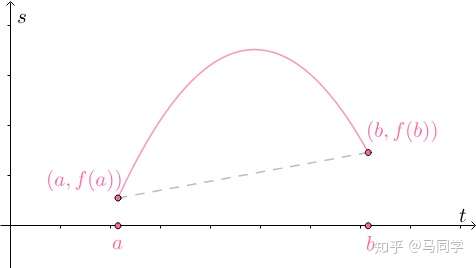
可以据此算出平均速度为：

比如算出来平均速度为 ，平均速度是由瞬时速度叠加的结果，那么路程中的瞬时速度可能为：

• 匀速前进：那么整个路程的瞬时速度必然全为
• 变速前进：整个路程的瞬时速度必然有大于、等于、小于 的情况

下面是变速前进的速度变换动画（蓝色为大于，闪烁为平行即等于，绿色为小于）：

如果限速 ，那么根据汽车的平均速度为 ，就可以判定路程中必然至少有一个点超速。

约瑟夫·拉格朗日伯爵，法国籍意大利裔数学家和天文学家，以他命名的拉格朗日中值定理就可以在数学层面解释刚才的现象。

2.1 拉格朗日中值定理

设函数满足以下两个条件：

• 在闭区间 上连续
• 在开区间 上可导

则存在 ，使得

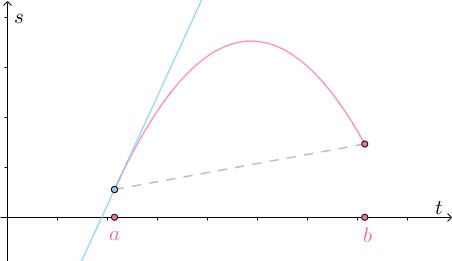
这个定理的几何意义就是，至少存在一点的切线与端点的连线平行；物理意义是，至少存在一点的速度与平均速度相等：

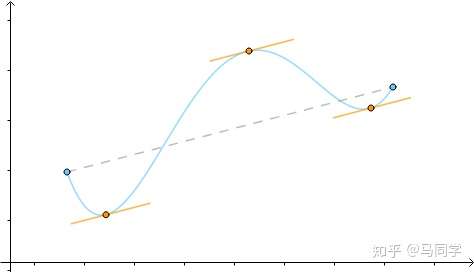
把它旋转一下，使得 ：

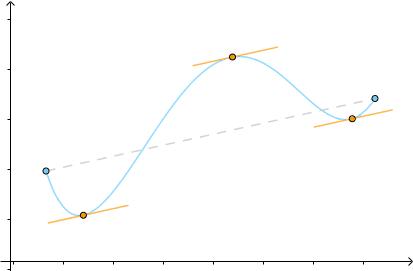
得到的就是罗尔中值定理，可见罗尔是拉格朗日的特例：

3 柯西中值定理

3.1 二维空间中的运动

之前讨论的是一维空间中的运动，下面来看看二维空间中的运动（关于这点，可以参看课程中“参数方程求导与相关变化率”这一节）。假设参数方程：

描述了一个二维空间中的运动：

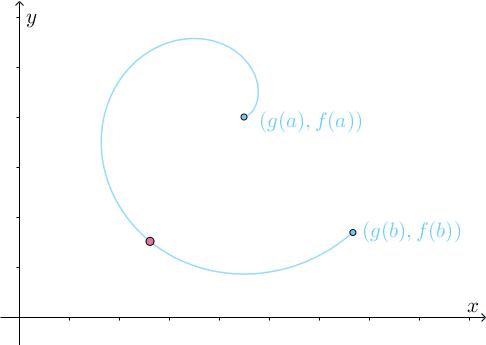
为了方便描述，令 、 ，那么上图描述的就是 时刻在 位置， 时刻运动到了 位置。向量 就表明了最终的运动方向：

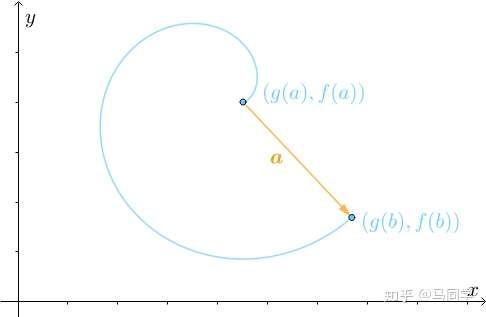
仔细分析此运动过程，刚开始的时候，速度 的方向与 相反，也就是说点是反着走的：

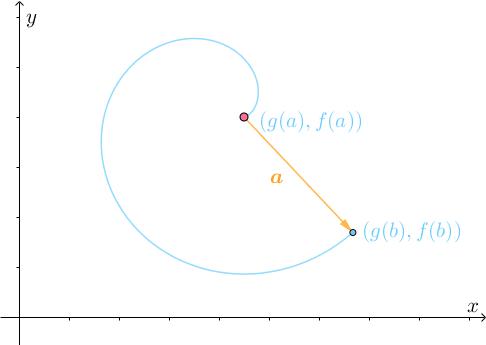
所以需要不断转弯调整：

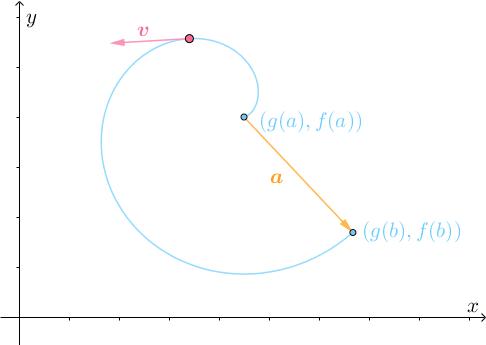
最终才能到达目的地：

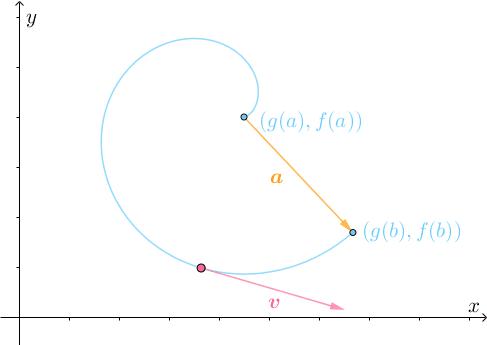
容易想象，在转弯调整的过程中，必然会有 和 同向的时刻，比如 时刻：

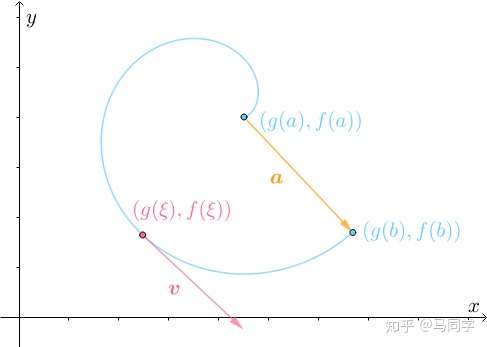
那么两者所在直线必然也平行：

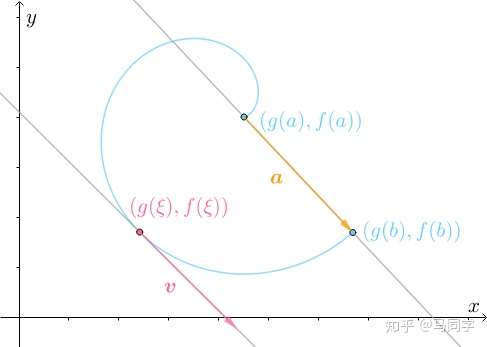
此时， 所在直线的斜率：

以及 所在直线的斜率（根据参数方程的求导法则）：

必然相等：

这就是柯西中值定理。

3.2 定理

设函数满足以下条件：

• 在闭区间 上连续
• 在开区间 上可导
• 有：

则存在 ，使等式

成立。

 

可以把 组合成参数方程：

这样柯西中值定理就有类似于拉格朗日中值定理一样的几何意义：

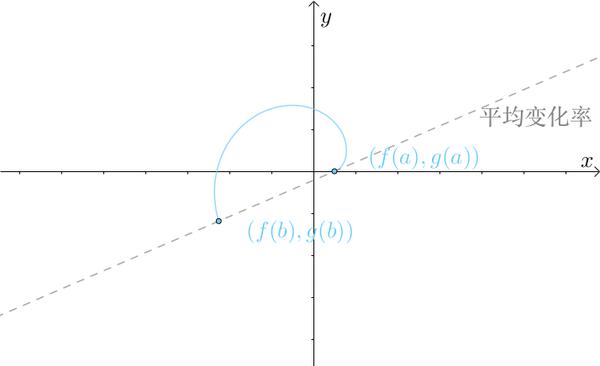
如果：

那么柯西中值定理就变为了拉格朗日中值定理，所以拉格朗日又是柯西的特例。

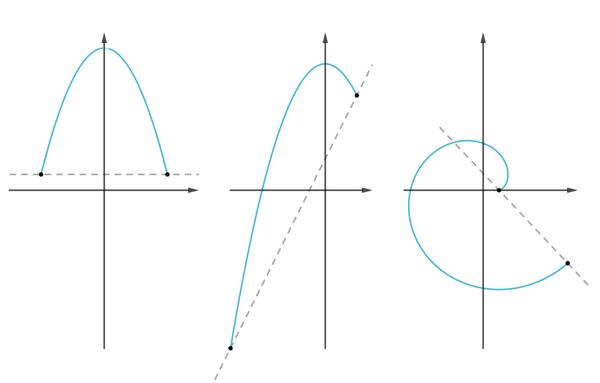
4 总结

三大微分中值定理的联系与区别：

本文为微分中值定理的节选，因为格式问题，还有一些证明、扩展没有贴上来，可以到原文去查看。

标签：拉格朗,定理,微分,柯西,可导,开区间,日中值,三大
来源： https://www.cnblogs.com/wkfvawl/p/12209871.html