11.8听课记录 && FFT
作者:互联网
FSYo讲数学+FFT,Orz
前置
傅里叶变换
(这里傅里叶变换不理解不影响FFT的学习)
先看 3B1B的傅里叶变换
泰勒展开,是用一个多项式去拟合一个函数 \(x_0\) 处的值,在较小的范围内能够比较接近。所以需要做到每次求导都和原函数相同,于是有
\[g(x)=f(x_0)+f'(x_0)(x-x_0)+\frac{f''(x_0)(x-x_0)^2}{2}+\frac{f'''(x_0)(x-x_0)^3}{6}+\cdots+\frac{f^{(n)}(x_0)(x-x_0)^n}{n!}+\cdots \]分母是后面的 \((x-x_0)^n\) 求导所产生的常数带来的影响。这样求每阶导都与原函数相同。
我们泰勒展开 \(e^{ix},isinx,cosx\),其中 \(i\) 是复数,分别得到:
\[\begin{align*} &e^{ix}=1+ix-\frac{x^2}{2!}-\frac{ix^3}{3!}+\frac{x^4}{4!}+\frac{ix^5}{5!}\cdots\\ &i\sin x=\frac{ix}{1!}-\frac{ix^3}{3!}+\frac{ix^5}{5!}-\frac{x^7}{7!}\cdots\\ &\cos x=1-\frac{x^2}{2!}+\frac{x^4}{4!}-\frac{x^6}{6!}\cdots \end{align*} \]可以发现 \(e^{ix}=\cos x+i\sin x\),这就是欧拉公式。
将 \(\pi\) 带入 \(x\) 就可以得到 \(e^{i\pi}+1=0\)
\(e^{ix}=\cos x+i\sin x\) 在复平面上就可以形象地理解成一个圆。随着 \(x\) 增大,\(e^{ix}\) 就在绕着圆旋转。
于是我们就能更清晰地理解傅里叶变换公式
\[\int_{t1}^{t2}g(t)e^{-2\pi ift}\mathrm dt \]如果写成离散形式并用 \(O(n^2)\) 计算就是离散傅里叶变换(DFT),使用神奇的单位根优化做到 \(O(n\log n)\) 计算就是我们的快速傅里叶变换(FFT)。
复数运算
一个复数 \(z=a+bi\),其中 \(a\) 是他的实部,\(b\) 是他的虚部,\(i\) 称为虚部单位。
一个复数 \(z=a+bi\) 的共轭复数是 \(\bar{z}=a-bi\) 。
复数有四则运算
\[\begin{align*} &(a\pm bi)\pm (c\pm di)=(a\pm c)\pm (b\pm d)i\\ &(a+b_i)(c+d_i)=(ac-bd)+(ad+bc)i\\ &\frac{a+b_i}{c+d_i}=\frac{(a+b_i)(c-d_i)}{(c+d_i)(c-d_i)}=\frac{(ac+bd)+(bc-ad)i}{c^2+d^2} \end{align*} \]多项式卷积
\[h(k)=\sum_{i+j=k}f(i)g(j) \]直接做显然是 \(O(n^2)\).
拉格朗日插值
(这里拉格朗日插值不理解不影响FFT的学习)
根据点值插出多项式的算法.
构造出 \(n\) 个函数,使得第 \(i\) 个函数只在 \(x=x_i\) 时有值为 \(y_i\),再将这 \(n\) 个函数求和。
由于次数为 \(n-1\) 且过这 \(n\) 个点的多项式函数只有一个,所以这个求和的函数就是那个正确的。
时间复杂度 \(O(n^2)\),使用高斯消元是 \(O(n^3)\).
\[f(x)=\sum_{i=1}^n y_i\prod_{j\ne i}^n \frac{x-x_j}{x_i-x_j} \]单位复根
\(n\) 次单位复根是满足 \(w^n=1\) 的复数 \(w\),显然这样的 \(w\) 有 \(n\) 个,均匀分布在复平面的单位圆上。
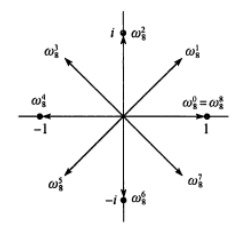
我们在欧拉公式 \(e^{ix}=\cos x+i\sin x\) 中,把 \(2\pi\) 带入 \(x\),可以得到 \(e^{2i\pi}=1\),那么 \(w=e^{\frac{2\pi i}{n}}\),将这个 \(w\) 记做主次单位根 \(w_n^1\),那么其他的单位根就是 \(w_n^k=e^{\frac{2\pi ik}{n}}(0\leq k<n)\),显然 \(w_n^0=1\)。
FFT
快速傅里叶变换(FFT)用于 \(O(n\log n)\) 时间内求两个多项式之积。
我们有两个多项式,(项数不同用 \(0\) 补足)
\[A(x)=a_0+a_1x+a_2x^2+a_3x^3+\cdots a_nx^n\\ B(x)=b_0+b_1x+b_2x^2+b_3x^3+\cdots b_nx^n \]直接做是无法 \(O(n\log n)\) 做的,于是我们找到两个多项式的点值表达式
\[A(x)=(x_0,y_0),(x_1,y_1),\cdots,(x_n,y_n)\\ B(x)=(x_0,y'_0),(x_1,y'_1),\cdots,(x_n,y'_n) \]那么他们相乘得到的多项式是
\[C(x)=(x_0,y_0y'_0),(x_1,y_1y'_1),\cdots,(x_n,y_ny'_n) \]也就是能够在 \(O(n)\) 时间内做乘法。
所以我们只需要能够将系数表达式快速转成点值表达式,以及将点值表达式快速转成系数表达式的办法。
\(O(n\log n)\) 求点值
我们需要将大于 \(2n\) 个点带入多项式计算点值,这里我们将单位根带入多项式求点值,并强制选 \(2^t\) 个单位根,也就是保证 \(n\) 是 \(2\) 的幂,那么这些单位根是 \(w_{2^t}^k=e^{\frac{2\pi ik}{2^t}}(0\leq k<2^t)\),看起来很麻烦,所以还是把 \(2^t\) 写成 \(n\)。
\[w_n^k=e^{\frac{2\pi ik}{n}}(0\leq k<n). \]显然有 \(w_n^j\times w_n^k=w_n^{(j+k)\%n}\)。
那么多项式 \(A(x)\) 的点值就是:
\[\begin{align*} &A(w_n^0)=a_0+a_1+a_2+\cdots+a_{n-1}\\ &A(w_n^1)=a_0+a_1w_n^1+a_2w_n^2+\cdots+a_{n-1}w_n^{n-1}\\ &A(w_n^2)=a_0+a_1w_n^2+a_2w_n^4+\cdots+a_{n-1}w_n^{2(n-1)}\\ &A(w_n^3)=a_0+a_1w_n^3+a_2w_n^6+\cdots+a_{n-1}w_n^{3(n-1)}\\ &\vdots \end{align*} \]考虑将每个点值按奇偶分开,比如
\[A(w_n^i)=(a_0+a_2w_n^{2i}+a_4w_n^{4i}+\cdots+a_{n-2}w_n^{(n-2)i})+(a_1w_n^i+a_3w_n^{3i}+\cdots+a_{n-1}w_{n-1}^{(n-1)i}) \]发现右边可以提一个 \(w_n^i\),于是
\[A(w_n^i)=(a_0+a_2w_n^{2i}+a_4w_n^{4i}+\cdots+a_{n-2}w_n^{(n-2)i})+w_n^i(a_1+a_3w_n^{2i}+\cdots+a_{n-1}w_{n-1}^{(n-2)i}) \]然后可以把左边视为系数为 \(a_0,a_2,a_4,\cdots,a_{n-2}\),带入 \(x\) 的为 \(w_n^{2i}\) 的一个项数是 \(\frac n2\) 的多项式,记为 \(FL(w_n^{2i})\),把右边视为系数为 \(a_1,a_3,a_5,\cdots,a_{n-1}\),带入 \(x\) 的为 \(w_n^{2i}\) 的一个项数是 \(\frac n2\) 的多项式,记为 \(FR(w_n^{2i})\),然后 \(w_n^{2i}=w_{n/2}^{i}\) ,所以相当于带入 \(w_{n/2}^{i}\)。(这就是强制 \(n=2^t\) 的原因)
所以我们要算 \(A(w_n^i)\) 的点值,只需要算 \(FL(w_{n/2}^i)\) 和 \(FR(w_{n/2}^i)\) 的点值,然后
\[A(w_n^i)=FL(w_{n/2}^i)+w_n^iFR(w_{n/2}^i) \]我们以 \(n=8\) 为例把每个点值的算式写出来
\[\begin{align*} &A(w_n^0)=FL(w_{n/2}^0)+w_n^0FR(w_{n/2}^0)\\ &A(w_n^1)=FL(w_{n/2}^1)+w_n^1FR(w_{n/2}^1)\\ &A(w_n^2)=FL(w_{n/2}^2)+w_n^2FR(w_{n/2}^2)\\ &A(w_n^3)=FL(w_{n/2}^3)+w_n^3FR(w_{n/2}^3)\\ &A(w_n^4)=FL(w_{n/2}^0)+w_n^0FR(w_{n/2}^0)\\ &A(w_n^5)=FL(w_{n/2}^1)+w_n^1FR(w_{n/2}^1)\\ &A(w_n^6)=FL(w_{n/2}^2)+w_n^2FR(w_{n/2}^2)\\ &A(w_n^7)=FL(w_{n/2}^3)+w_n^3FR(w_{n/2}^3)\\ \end{align*} \]注意到并不需要每个单位根的点值都这样算一遍,因为前面一半的 \(FL,FR\) 和后面一半是一样的,所以我们每次的计算规模是减半的,把所有单位根的点值一起计算,每次计算时 \(O(n)\),所以总的时间复杂度是 \(T(n)=2T(\dfrac n2)+O(n)=O(n\log n)\),我们就成功地在 \(O(n\log n)\) 的时间内把系数表达式转成点值表达式了。以上称为快速傅里叶变换。
\(O(n\log n)\) 求系数
·设原本的多项式是
\[A(w_n^x)=\sum_{i=0}^{n-1}a_iw_n^{xi} \]我们对他进行傅里叶变换,得到 \(n\) 个点值,设 \(A(w_n^i)\) 为 \(b_i\),我们把这些 \(b_i\) 当做系数再做一次 FFT,得到
\[C(w_n^x)=\sum_{i=0}^{n-1}b_iw_n^{xi} \]把 \(b_i\) 换成多项式的式子
\[C(w_n^x)=\sum_{i=0}^{n-1}w_n^{xi}\sum_{j=0}^{n-1}a_jw_n^{ij} \]套路交换求和号
\[C(w_n^x)=\sum_{j=0}^{n-1}a_j\sum_{i=0}^{n-1}w_n^{i(j+x)} \]利用单位根的性质,发现在复平面的单位元上,只有 \(j+x=n\) 时,后面的 \(\sum\) 才有值为 \(n\),否则所有单位根之和总是 \(0\),(特殊情况是 \(x=0\),此时只有 \(j=0\) 才有值为 \(n\)),所以我们发现
\[\begin{align*} &C(w_n^0)=na_0\\ &C(w_n^1)=na_{n-1}\\ &C(w_n^2)=na_{n-2}\\ &\vdots\\ &C(w_n^{n-1})=na_1 \end{align*} \]所以我们对用快速傅里叶变换所求出的点值当成系数再做一遍快速傅里叶变换,再得到的点值就可以表示出原本的系数了。以上称为快速傅里叶逆变换。
优化
如果递归地FFT,常数会很大,我们把 FFT 的递归写出来
发现每个位置在 FFT 最后一层的位置是他二进制反转后的位置。
我们可以 \(O(n)\) 预处理出每个位置最终的位置 rev[i] 然后从下往上合并上去,会比递归快很多。
预处理
int bit=0;
while ((1<<bit)<n)bit++;
fo(i,0,n-1){
rev[i]=(rev[i>>1]>>1)|((i&1)<<(bit-1));
if (i<rev[i])swap(a[i],a[rev[i]]);//不加这条if会交换两次(就是没交换)
}
反正很神妙就对了。
还有不会的蝴蝶变换
标签:ix,frac,多项式,FFT,cdots,点值,&&,11.8,FL 来源: https://www.cnblogs.com/llmmkk/p/15530880.html