首页 > TAG信息列表 > 骑士
P2669 [NOIP2015 普及组] 金币(平台移动)
国王将金币作为工资,发放给忠诚的骑士。第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式会一直这样延续下去:当连续 nn 天每天收到 nn 枚金币后,骑士会在[SCOI2005]骑士精神
link 和八数码难题是一样的,反正都是把一些棋子挪来挪去。这道题对估价函数有更高的依赖性,不开会只有20分(8个TLE),开了就能跑到100ms。好玄学啊。 #include<bits/stdc++.h> //#define feyn using namespace std; inline void read(int &wh){ wh=0;int f=1;char w=getchar(); while([ZJOI2008] 骑士
P2607 [ZJOI2008] 骑士 思路 显然抽象成图, 由每个骑士向他最讨厌的骑士 每个节点对应一条边, 即 \(n\) 个节点, \(n\) 条边, 并且没有说任意两点相联通, 所以是基环森林. 那么很容易就能想到基环树形dp 状态 显然对于每个节点有两种选择 选( \(1\) ) 不选( \(0\) ) 很容易设计:[20220324联考] 小 W 与骑士
前言 典中典中典之没做过典中典套路题两双手。 题目 没有链接 如果从 \((x,y)\) 出发,每次可以走到 \((x+ax,y+ay)\) 或 \((x+bx,y+by)\),起点是 \((0,0)\),终点是 \((X,Y)\),有 \(n\) 个点 \((x_i,y_i)\) 是障碍点不能走,问方案数,对 \(10^9+7\) 取模。如果路线无限多,输出 -1。 多组数OpenJudge - 1490:A Knight‘s Journey
骑士厌倦了一次又一次地看到相同的黑白方块,并决定环游世界。每当骑士移动时,它都是一个方向上的两个正方形和一个垂直于此方向的正方形。骑士的世界就是他所生活的棋盘。我们的骑士住在一个棋盘上,这个棋盘的面积比普通的8 * 8棋盘小,但它仍然是矩形的。你能帮助这个冒险的骑士制C语言丨约瑟夫问题(约瑟夫环)
约瑟夫问题又称为约瑟夫环,约瑟夫问题有很多变种。本文就以几个经典的约瑟夫问题介绍其几种解法。 问题1:鲁智深吃馒头。据说,鲁智深一天中午匆匆来到开封府大相国寺,想蹭顿饭吃,当时大相国寺有99个和尚,只做了99个馒头。智清长老不愿得罪鲁智深,便把他安排在一个特定位置,之后对所有7-7 国王的金币 (10 分)
国王将金币作为工资,发放给忠诚的骑士。 第1天,骑士收到1枚金币,1 之后两天,每天收到2枚金币,1 2 2 之后3天每天收到3枚金币…….。1 2 2 3 3 3 这种工资发放模式一直延续。 求给定天数,计算一个骑士获得的金币。 输入格式: 输入发金币的天数 输出格式: 输出获得的金币总数 输入样例:POJ-2942 Knights of the Round Table
题意:一些骑士要进行圆桌会议,每桌要坐奇数个人。互相憎恨的骑士不能相邻。现给出骑士之间的憎恨关系(双向),求删去多少人后,能正常开会。 解:将互相不憎恨的骑士连边,也就是补图。注意每个骑士一定不憎恨他自己(离散数学老师:和自己达成和解,这样挺好的)想想下学期就不能听他扯淡了还有点难过uva11292
你的王国里有一条n个头的恶龙,你希望雇佣一些骑士把它杀死(即砍掉所有头)。村里有m个骑士可以雇佣,一个能力值为x的骑士可以砍掉恶龙一个直径不超过x的头,且需要支付x个金币。如何雇佣骑士才能砍掉龙的所有头,且需要支付的金币最少?注意,一个骑士只能砍一个头。(且不能被雇佣两次)。 输骑士周游问题
算法 1. 骑士周游问题 马踏棋盘算法也被称为骑士周游问题 将马随机放在国际象棋的 8x8 棋盘中[0~7][0~7]的某个方格中,马鞍走起规则(马走日字)进行移动。要求每个方格只进入一次,走遍棋盘上全部64个方格 3. 会使用到图的遍历算法(DFS)+ 贪心算法优化 1.1 普通方法 package c【蓝桥杯C++练习】每日一练13-编程题
国王将金币作为工资,发放给忠诚的骑士。第一天,骑士收到一枚金币;之后两天(第二天和第三天)里,每天收到两枚金币;之后三天(第四、五、六天)里,每天收到三枚金币;之后四天(第七、八、九、十天)里,每天收到四枚金币……这种工资发放模式会一直这样延续下去:当连续N天每天收到N枚金币后,骑士会在之死循环与break、continue
通过前面循环的学习,我们已经知道了什么叫死循环,例如: python代码: while True: print(1) C++代码: #include <iostream> using namespace std; int main() { while (true) { cout << 1 << endl; } return 0; } 以上代码会一直打印1,不会停下来。今天要讲的bAcer 暗影骑士擎 安装深度学习环境
深度学习安装步骤可以概括为以下三步: 第一步 安装Anaconda 1.1 可以参考 史上最全最详细的Anaconda安装教程 1.2创建一个新的虚拟环境环境 激活刚刚创建的环境 列出你所有创CF1574 C. Slay the Dragon(三分)
目录 Description State Input Output Solution Code Description 有 \(n\) 个骑士,都有一个能力值 \(a[i]\), 有 \(m\) 个怪物,怪物有两个属性 \(x, y\) ,你可以花费 \(1\) 个金币使得任意一个骑士的能力值 \(+1\),最后派出一个骑士,满足这个骑士 \(a[i]>=x\),其余骑士的能力值2607-骑士
基环树上的dp。 题目给出的图是一个一个所有点的出度为一的有向图,这样的图可以形成多棵基环内向树。要求在树上选一些不相邻的点,让他们的点权和最大。 发现在图是一棵树的情况下这题就是经典题没有上司的舞会,考虑把基环树边拆成树,由于题目的构造方法,每一个弱联通块内最多只有一个老曹骑士(bfs)
老曹骑士 题目大意 给你一个网格,然后有一些点要走,问你从一个要走的出发走过所有要走的点在回到你出发的点。 要用的最小步数,而且每次走是像象棋的马一样走“日”字形。 思路 你看到范围,不难想到其实可以直接 bfs。 状态就是 f[AHOI2014/JSOI2014]骑士游戏
题目链接 问题分析 如果这个图是个DAG,那么问题就简单了。按照拓扑序的逆序做DP即可。 那么问题就在于环。于是借助SPFA的想法,更新某个节点后向它的父亲拓展,直至不能更新。 这里需要注意把可能要被更新的节点入队,而不是确定要被更新的点,否则可能TLE。具体见参考程序。 参考程序 #inP3355 骑士共存问题
骑士共存问题 题目描述 在一个 $n \times n$ 个方格的国际象棋棋盘上,马(骑士)可以攻击的棋盘方格如图所示。棋盘上某些方格设置了障碍,骑士不得进入。 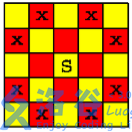 对于给定的 $n \times n$ 个方格的国际象棋棋盘和障碍标志,计算棋盘上最多可以ZJOI 2008 骑士
ZJOI 2008 骑士 题意:https://www.luogu.com.cn/problem/P2607 显然的图论题。我们把每个骑士看作一个点,将每个骑士与他厌恶的骑士连一条无向边。然后就会发现这题跟 没有上司的舞会(https://www.luogu.com.cn/problem/P1352) 有点类似。如果一个点选了,那么所有与它相连的点就[ZJOI2008] 骑士
[ZJOI2008]骑士 题意简述 求基环树森林中的最大权独立集。 数据范围:\(1\le n\le 10^6\)。 知识要点 树形 DP 基环树 题目分析 题目一上眼,是一个显然的最大权独立集问题。这是树形 DP 中选择节点类的题目,如果整个图构成一颗树的话,可以直接套路地定义状态 \(dp[i][0]/dp[i][1Java P2669 [NOIP2015 普及组] 金币 洛谷入门题
P2669 [NOIP2015 普及组] 金币 题目描述 国王将金币作为工资,发放给忠诚的骑士。第一天,骑士收到一枚金币;之后两天(第二天和第三天),每天收到两枚金币;之后三天(第四、五、六天),每天收到三枚金币;之后四天(第七、八、九、十天),每天收到四枚金币……;这种工资发放模式会一直这样延续下去:当Revit模型轻量化方法
一、背景 小伙伴们在做Revit二次开发时,是否有模型轻量化的需求呢? 二、解决思路 骑士特意录制了一个视频来说明如何做https://www.bilibili.com/video/BV1z54y1V7Dh 如果视频链接失效:在bilibili中搜索:Revit的Web之旅简介 第一步:在Revit中使用IexportContext接口导出对应模型入手评测 暗影骑士龙和暗影骑士擎哪个更值得入手
宏碁暗影骑士龙:其屏幕的尺寸大小为15.6英寸,分辨率为1920×1080,屏幕比例为16:9,IPS屏,72%NTSC屏幕色域,144HZ屏幕刷新率。其中rtx3070版,分辨率为2.5k,刷新率为165Hz 选暗影骑士龙还是暗影骑士擎这些点很重要看过你就懂了http://www.adiannao.cn/dy 宏碁暗影骑士擎:其屏幕尺寸,分辨率Codeforces Round #700 (Div. 2) B(简单思维)
B 思路: 骑士有一个生命值,先把所有怪兽的伤害值减掉,然后加上所有怪兽的最大攻击值,判断其与0的大小。为什么呢?可能最后一次骑士打死怪兽之后就会死亡,只要加上最大的攻击值就会回到进行最后一次攻击前的状态,如果此时骑士的生命值大于0,就可以打死所有怪兽。 注意:数据要开ll,因Revit模型如何在网页上显示
一、背景 小伙伴们在做Revit二次开发时,是否需要把Revit模型放到网页上去显示呢? 二、解决方案 为了帮助大家解决这个问题,骑士专门出了一个教学视频,包括以下内容: Revit模型格式转换;模型轻量化;前端(HTML/JavaScript/CSS/Three.js)技术;Revit模型和网页如何交互等; … 链接如下: ht