[ZJOI2008]骑士

---

题意简述

求基环树森林中的最大权独立集。

数据范围：\(1\le n\le 10^6\)。

---

知识要点

• 树形 DP
• 基环树

---

题目分析

题目一上眼，是一个显然的最大权独立集问题。这是树形 DP 中选择节点类的题目，如果整个图构成一颗树的话，可以直接套路地定义状态 \(dp[i][0]/dp[i][1]\)，表示第 \(i\) 个节点，是否选择，得到的以 \(i\) 为根节点的树中的最大权独立集。

容易写出状态转移方程：

\[\begin{aligned}\begin{cases} dp[i][0]&=\sum\limits_{x\in son[i]} \max\Big(dp[x][0],dp[x][1]\Big)\\dp[i][1]&=\sum\limits_{x\in son[i]}dp[x][0]\end{cases}\end{aligned}\]

边界条件：\(dp[i][0]=0,dp[i][1]=val[i]\)

但在此题中，我们需要在基环树森林中求最大权独立集。注意到图中仅有 \(n\) 个点 \(n\) 条边，因此图中有且仅有一个环。而断开这个环上的任意一条边，剩下的点和边就形成了一颗树，我们就可以用树形 DP 进行统计了。

要注意，虽然我们把边断开了，但是边两端的节点 \(u\) 和 \(v\) 仍然不能同时选择。因此我们需要采取强制措施，对断边的两端 \(u\) 和 \(v\) 都跑一次树形 DP，并且在从 \(u\) 开始时不经过 \(v\)，从 \(v\) 开始时不经过 \(u\)。

为了便于操作，我们从骑士的敌人向骑士连一条有向边，因为一名骑士只有一个自己最厌恶的骑士，因此连边后整张图就构成了基环外向树。因此当跑树形 DP 重新经过出发点 \(u\) 时，那么这条边的起点就是 \(v\)，也就是不能选的节点。出现此种情况时，我们设置 \(dp[v][1]=-inf\)，就可以防止选取点 \(v\) 了。

如何找到环？在这里借用一下 hkr04 洛谷题解 中的图片：

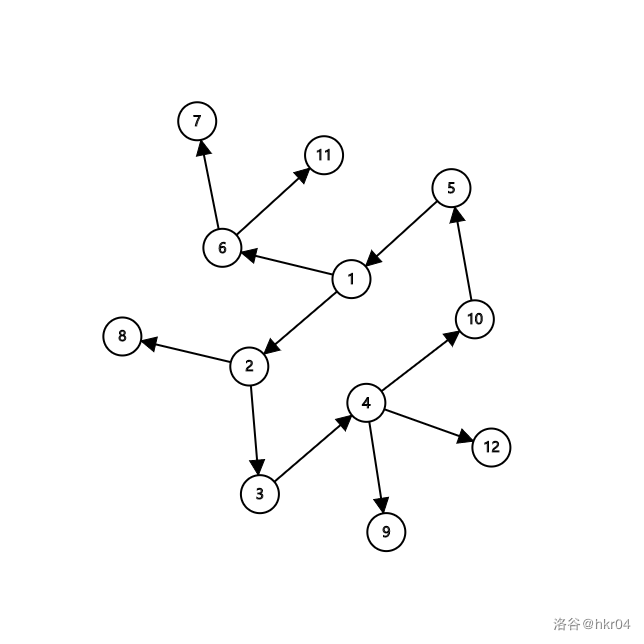
在找环时，当我们发现 7 号点没有被访问时，说明这棵树的答案仍为统计。我们从该点往回回到环上，最终到达了 2 号点。

---

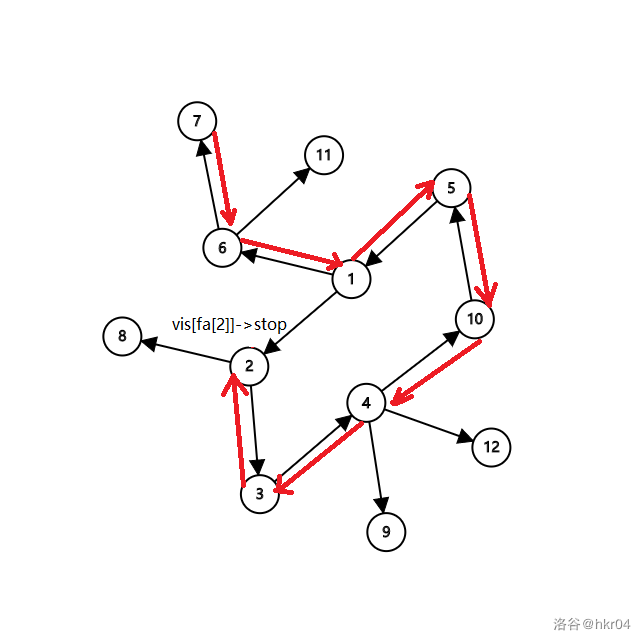
代码展示

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const ll inf=0x3f3f3f3f3f3f3f3f;
const int M=1e6+5;

int n,fa[M],p0;
bool vis[M];
ll val[M],dp[M][2],ans;

struct edge
{
	int to,nxt;
}e[M];
int hd[M],cnt;
void add(int x,int y)
{
	e[++cnt]=(edge){y,hd[x]};
	hd[x]=cnt;
}

void dfs(int u)
{
	vis[u]=true;
	dp[u][0]=0,dp[u][1]=val[u];// 边界条件
	
	for(int i=hd[u];i;i=e[i].nxt)
	{
		int v=e[i].to;
		if(v==p0)dp[v][1]=-inf;// 强制控制v不选
		else
		{
			dfs(v);
			dp[u][0]+=max(dp[v][0],dp[v][1]);
			dp[u][1]+=dp[v][0];// 状态转移
		}
	}
}

void find_circle(int u)
{
	vis[u]=true;
	while(!vis[fa[u]])
	{
		u=fa[u];
		vis[u]=true;
	}
	p0=u,dfs(u);
	ll now=max(dp[u][0],dp[u][1]);
	u=fa[u];//执行该语句前有 vis[fa[u]]=true，因此u和fa[u]就是需要断边的两端
	p0=u,dfs(u);
	now=max(now,max(dp[u][0],dp[u][1]));
	ans+=now;
}

int main()
{
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
	{
		scanf("%lld%d",&val[i],&fa[i]);
		add(fa[i],i);//注意从敌人连向自己
	}
	for(int i=1;i<=n;i++)
		if(!vis[i])//被统计过了就不搜了
			find_circle(i);
	printf("%lld",ans);
	return 0;
}

标签：vis,int,max,fa,DP,ZJOI2008,骑士,dp
来源： https://www.cnblogs.com/cyl06/p/AC1000.html