四元数阅读文档笔记记录

原文档：https://link.zhihu.com/?target=https%3A//krasjet.github.io/quaternion/

一、笔记

1、p11

这里的平移，如果轴不经过原点，那么，在平移过程中，要旋转的点也是跟随轴一起平移的，它们可以看作一个整体。也就是说，先将轴和要围绕这轴旋转的点一起平移到轴经过原点的地方，然后进行相应的旋转操作，之后再将轴和点一起平移回去。

2、p12

2.1

三维中，一个轴的坐标，其实是代表这个轴的线段的末端点的坐标，而且，这里我们是已经假设了轴是经过原点的。

2.2

Q：为什么说在三维空间中定义一个方向只需要用到两个量就可以了？（与任意两个坐标轴之间的夹角）？
A：因为我们在微积分中学过，\(cos^2\alpha + cos^2 \beta + cos^2 \gamma = 1\).

3、p13

以下是关于上面的正交投影式子的简要说明。

利用正交性，可得：\(\displaystyle \textbf{u} \cdot (\textbf{v} - \frac{\textbf{u}}{\left| \textbf{u} \right|} \cdot \left| \textbf{v} \right| \cdot cos \alpha) = 0\)，其中，\(\alpha\) 指 \(\textbf{u}\) 与 \(\textbf{v}\) 的夹角。
化简，得：\(\displaystyle \left| \textbf{v} \right| \cdot cos \alpha = \frac{\textbf{u} \cdot \textbf{v}}{\textbf{u} \cdot \textbf{u}}\)，这里，\(\left| \textbf{v} \right| \cdot cos \alpha\) 表示 \(\textbf{v}_{||}\) 的模，所以，\(\displaystyle \frac{\textbf{u} \cdot \textbf{v}}{\textbf{u} \cdot \textbf{u}} \textbf{u}\) 表示 \(\textbf{v}_{||}\)。

4、p21

这里涉及到向量的叉乘，回到学校之后，利用教材再进行详细复习。

5、p25

“我们可以很容易地将前面的 \(\textbf{v}^{'}_{\perp}\) 和 \(\textbf{v}_{\perp}\) 替换为 \(v^{'}_{\perp}\) 和 \(v_{\perp}\)” 这里的 \(v^{'}_{\perp}\) 和 \(v_{\perp}\) 指的是 p24 中的纯四元数。

6、p38

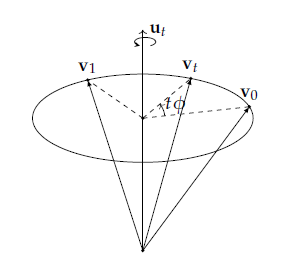
这里的角 \(\phi\) 应该是不定的，因为过 \(\textbf{v}_0\) 和 \(\textbf{v}_1\) 这两点的圆弧是不定的，但是，暂时可以这样理解，一旦确定（不妨）了一个圆弧，那么，相关的比例总是准确的。

7、p39

这里暂时可以用二维的向量点乘结果来辅助理解。我们知道，二维中，两个单位向量的点乘的结果是这两个向量的夹角的余弦值。这一点利用三角关系不难得出。

二、后记

这篇文档是知乎的一个用户分享的，当然，他也是篇文档的作者，我认为，这篇文档写得比较通俗易懂，同时不失其严谨性，用来了解四元数，应该说是相当合适。

关于这篇文档，第 6 章的部分我没有读懂，但是，对于四元数这一整体还是有了一定的把握，至少，再次学习 Unity 时，不会因为这个而磕磕绊绊了。

标签：cos,cdot,笔记,textbf,四元,perp,文档,alpha
来源： https://www.cnblogs.com/fanlumaster/p/14398840.html