首页 > 其他分享> > 高等代数6 线性空间

高等代数6 线性空间

2020-08-28 22:02:50 作者：互联网

高等代数6 线性空间

高等代数6 线性空间
集合
映射
线性空间
基变换与坐标变换
子空间
- 子空间的运算——交与和
- 子空间的直和
同构

集合

集合就是指作为整体看的一堆东西。组成集合的东西称为这个集合的元素。

映射

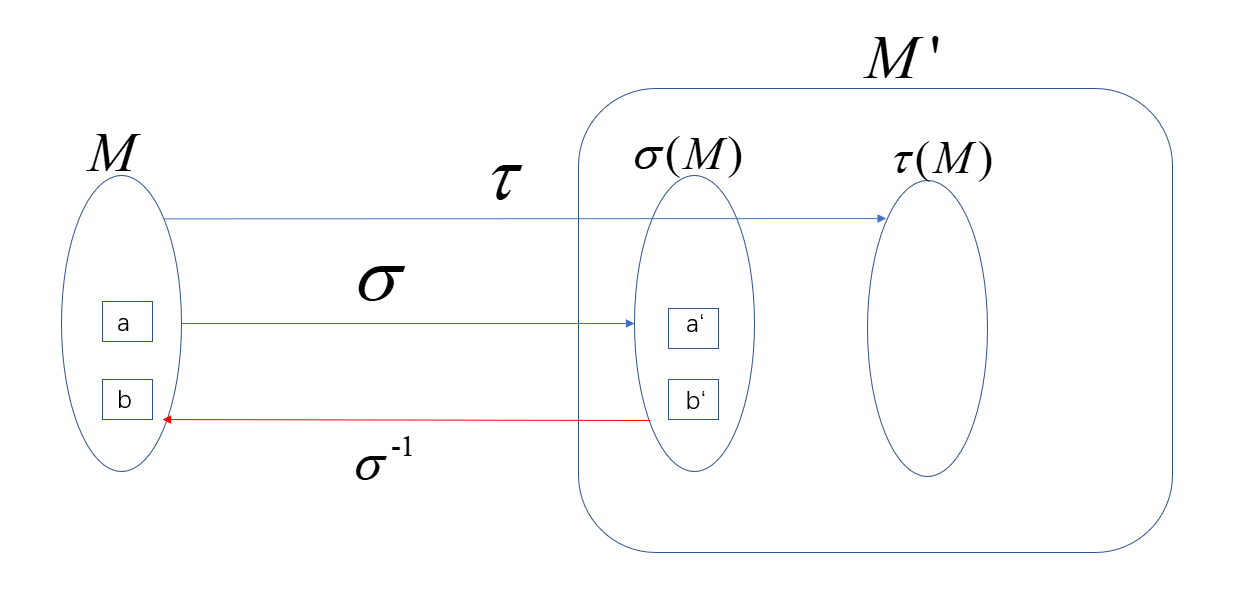
设$M,M'$是两个集合，集合$M$到集合$M'$的一个映射就是指一个法则，它使$M$中的每一个元素$a$都有$M'$中一个确定的元素$a'$与之对应。如果映射$\sigma(a)=a'$，$a'$称为$a$在映射$\sigma$下的像，而$a$称为$a'$在映射$\sigma$下的一个原像。

$M$到$M$自身的映射，有时也称为$M$到自身的变换。

集合$M$到集合$M'$的两个映射$\sigma$及$\tau$，若对$M$的每个元素$a$都有$\sigma(a)=\tau(a)$，则称它们相等，记作$\sigma=\tau$。
单位映射

设$M$是一个集合，定义 $\tau(a)=a,a\in M$

即$\sigma$把每个元素映射到它自身，称为集合$M$的恒等映射或单位映射，记作$1_M$，可以简记为$1$。
满射如果$\sigma(M)=M'$，映射$\sigma$就称为满射。
单射如果在映射$\sigma$下，$M$中不同元素的像也不同，即由$a_1 \neq a_2$，一定有$\sigma(a_1)\neq \sigma(a_2)$，那么映射$\sigma$就称为单射。
双射一个映射既是单射又是满射就称为双射，或$1-1$对应。
逆映射 对于$M$到$M'$的双射$\sigma$，我们可以定义它的逆映射，记为$\sigma^{-1}$。

对于映射我们可以定义乘法

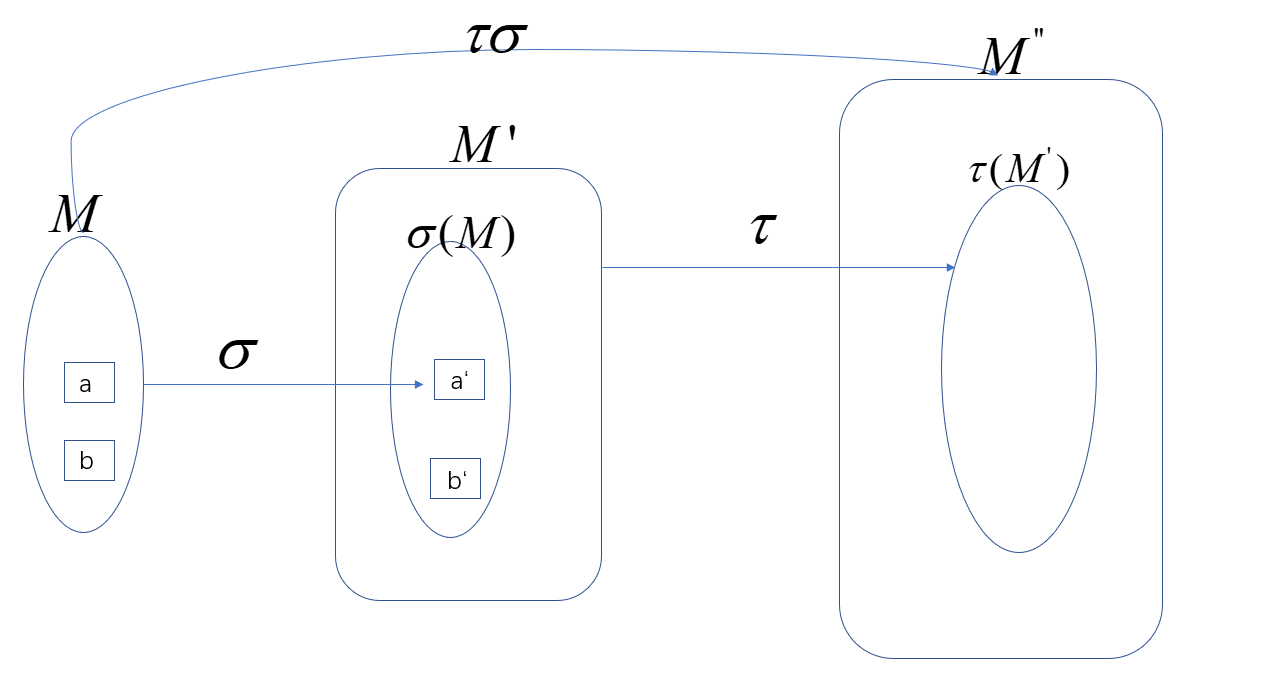
设$\sigma,\tau$分别是集合$M$到集合$M'$，$M'$到$M''$的映射，乘积$\tau\sigma$定义为

\[(\tau\sigma)(a)=\tau(\sigma(a)),a\in M \]

即相继执行$\sigma、\tau$的结果，$\tau\sigma$是$M$到$M''$的映射。

适合结合律 $(\psi \tau)\sigma=\psi(\tau\sigma)$

线性空间

定义

非空集合 数域$P$上的一个非空集合$V$
对加法和数乘有封闭性
- 给出一个加法法则，对于$V$中任意两个元素$\alpha$与$\beta$，在$V$中都有唯一的一个元素$\gamma$与它们对应，称为$\alpha$与$\beta$的和，记作$\gamma=\alpha+\beta$。
- 给出数量乘法运算，对于数域$P$中任一数$k$和$V$中任一元素$\alpha$，在$V$中都有唯一的一个元素$\delta$与它们对应，称为$k$与$\alpha$的数量乘积，记作$\delta=k\alpha$。
满足8条规则
- 加法满足下面四条规则：
  1. 加法交换律$\alpha+\beta=\beta+\alpha$;
  2. 加法结合律$(\alpha+\beta)+\gamma=\alpha+(\beta+\gamma)$；
  3. 零元素 在$V$中有一个元素$0$，对于$V$中任一元素$\alpha$都有$0+\alpha=\alpha$。$0$称为$V$中的零元素。
  4. 负元素 对于$V$中的每一个元素$\alpha$，都有$V$中的元素$\beta$，使得$\alpha+\beta=0$,。$\beta$称为$\alpha$的负元素。
- 数量乘法满足下面两条规则：
  1. 单位元素 $1 \alpha=\alpha$。
  2. $k(l\alpha)=(kl)\alpha$
- 数量乘法与加法满足下面两条规则
  1. $(k+l)\alpha=k\alpha+l\alpha$
  2. $k(\alpha+\beta)=k\alpha+k\beta$
在以上规则中$k,l$表示数域$P$中的任意数；$\alpha,\beta,\gamma$表示集合$V$中的任意元素。

线性空间中的元素也称为向量，线性空间也称为向量空间。

简单性质

零元素是唯一的。
负元素是唯一的。

利用负元素，定义减法：$\alpha-\beta=\alpha+(-\beta)$
$0\alpha=0,k0=0,(-1)\alpha=\alpha$
如果$k\alpha=0$，那么$k=0或\alpha=0$

线性相关与无关

单个向量$\alpha$是线性相关的充分必要条件是$\alpha=0$

两个以上向量$\alpha_1,\alpha_2,\cdots,\alpha_r$线性相关的充分必要条件是其中有一个向量是其余向量的线性组合。
如果向量组$\alpha_1,\alpha_2,\cdots,\alpha_r$线性无关，而且可以被$\beta_1,\beta_2,\cdots,\beta_s$线性表出，那么$r \leq s$。

两个等价的线性无关的向量组必定含有相同个数的向量。
如果向量组$\alpha_1,\alpha_2,\cdots,\alpha_r$线性无关，但向量组$\alpha_1,\alpha_2,\cdots,\alpha_r,\beta$线性相关，那么$\beta$可以被$\alpha_1,\alpha_2,\cdots,\alpha_r$线性表出，而且表示是唯一的。

维度

如果在线性空间$V$中有$n$个线性无关的向量，但是没有更多数目的线性无关的向量，那么$V$就称为是$n$维的。

如果在在线性空间$V$中有任意多个个线性无关的向量，那么$V$就称为是无限维的。

基、坐标

在$n$维线性空间$V$中，$n$个线性无关的向量$\varepsilon_1,\varepsilon_2,\cdots,\varepsilon_n$称为$V$的一组基。

设$\alpha$是$V$中任一向量，于是$\varepsilon_1,\varepsilon_2,\cdots,\varepsilon_n,\alpha$线性相关，因此$\alpha$可以被$\varepsilon_1,\varepsilon_2,\cdots,\varepsilon_n$线性表出：

\[\alpha=a_1\varepsilon_1+a_2\varepsilon_2+\cdots+a_n\varepsilon_n \]
其中系数$a_1,a_2,\cdots,a_n$是被向量$\alpha$和基$\varepsilon_1,\varepsilon_2,\cdots,\varepsilon_n$唯一确定的，这组数就称为$\alpha$在基$\varepsilon_1,\varepsilon_2,\cdots,\varepsilon_n$下的坐标，记为$(a_1,a_2,\cdots,a_n)$
定理

如果在线性空间$V$中有$n$个线性无关的向量$\alpha_1,\alpha_2,\cdots,\alpha_n$，且$V$中任一向量组都可以用它们线性表出，那么$V$是$n$维的，而$\alpha_1,\alpha_2,\cdots,\alpha_r$就是$V$的一组基。

基变换与坐标变换

在同一向量空间下，同一个向量在不同基下的坐标是不同的。

设$\varepsilon_1,\varepsilon_2,\cdots,\varepsilon_n$与$\varepsilon_1',\varepsilon_2',\cdots,\varepsilon_n'$是$n$维向量空间的两组基，它们的关系是

\[\begin{cases} \varepsilon_1'=a_{11}\varepsilon_1 +a_{12}\varepsilon_2+\cdots +a_{1n}\varepsilon_n \\ \varepsilon_2'=a_{21}\varepsilon_1 +a_{22}\varepsilon_2+\cdots +a_{2n}\varepsilon_n \\ \ \ \ \cdots \cdots \\ \varepsilon_n'=a_{n1}\varepsilon_1 +a_{n2}\varepsilon_2+\cdots +a_{nn}\varepsilon_n \\ \end{cases} \\ (\varepsilon_1',\varepsilon_2',\cdots,\varepsilon_n') =(\varepsilon_1,\varepsilon_2,\cdots,\varepsilon_n) \left ( \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{s1} & a_{s2} & \cdots & a_{sn} \\ \end{matrix} \right ) \\ A= \left ( \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{s1} & a_{s2} & \cdots & a_{sn} \\ \end{matrix} \right ) \]

设$\xi $在这两组基下的坐标分别是 $x_1,x_2,\cdots,x_n$与$ x_1,x_2,\cdots,x_n$

\[\xi=x_{1}\varepsilon_1 +x_{2}\varepsilon_2+\cdots +x_{n}\varepsilon_n =(\varepsilon_1,\varepsilon_2,\cdots,\varepsilon_n) \left ( \begin{matrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{matrix} \right ) \\ =x_{1}'\varepsilon'_1 +x_{2}\varepsilon'_2+\cdots +x'_{n}\varepsilon'_n =(\varepsilon'_1,\varepsilon'_2,\cdots,\varepsilon'_n) \left ( \begin{matrix} x'_{1} \\ x'_{2} \\ \vdots \\ x'_{n} \\ \end{matrix} \right ) \]

将(3)式带入(4)得

\[\left ( \begin{matrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{matrix} \right ) = \left ( \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{s1} & a_{s2} & \cdots & a_{sn} \\ \end{matrix} \right ) \left ( \begin{matrix} x'_{1} \\ x'_{2} \\ \vdots \\ x'_{n} \\ \end{matrix} \right ) \\ \left ( \begin{matrix} x'_{1} \\ x'_{2} \\ \vdots \\ x'_{n} \\ \end{matrix} \right ) = \left ( \begin{matrix} a_{11} & a_{12} & \cdots & a_{1n} \\ a_{21} & a_{22} & \cdots & a_{2n} \\ \vdots & \vdots & & \vdots \\ a_{s1} & a_{s2} & \cdots & a_{sn} \\ \end{matrix} \right )^{-1} \left ( \begin{matrix} x_{1} \\ x_{2} \\ \vdots \\ x_{n} \\ \end{matrix} \right ) \]

上式给出了在基变换（3）下向量的坐标变换公式。

子空间

数域$P$上线性空间$V$的一个非空集合$W$称为$V$的一个线性子空间（或简称为子空间），如果$W$对于$V$的两种运算也构成数域$P$上的线性空间。
定理子空间条件
- 线性空间$V$的非空子集合$W$
- $W$对于$V$中原有两种运算具有封闭性
  1. 如果$W$中包含向量$\alpha$，那么$W$就一定同时包含域$P$中的数$k$和$\alpha$的数量乘积$k\alpha$.
  2. 如果$W$中包含向量$\alpha，\beta$，那么$W$就同时包含$\alpha,\beta$的和$\alpha+\beta$
零子空间 在线性空间中，由单个的零向量所组成的子集合是一个线性子空间，叫做零子空间。
线性空间$V$本身也是$V$的一个子空间。
平凡子空间 零子空间和线性空间本身这两个子空间叫做平凡子空间。其他线性子空间叫做非平凡子空间。
由$\alpha_1,\alpha_2,\cdots,\alpha_r$生成的子空间

设$\alpha_1,\alpha_2,\cdots,\alpha_r$是线性空间$V$的一组向量，

不难看出，这组向量所有可能的线性组合$k_1\alpha_1+\alpha_2+\cdots+k_r\alpha_r$所构成的集合是非空的，

而且对这两种运算封闭

所以是$V$的一个线性子空间。

这个子空间叫做由$\alpha_1,\alpha_2,\cdots,\alpha_r$生成的子空间，记为$L(\alpha_1,\alpha_2,\cdots,\alpha_r)$
定理
1. 两个向量组生成相同子空间的充分必要条件是这两个向量组等价；
2. $L(\alpha_1,\alpha_2,\cdots,\alpha_r)$的维数等于向量组$\alpha_1,\alpha_2,\cdots,\alpha_r$的秩。
定理

设$W$是数域$P$上$n$维线性空间$V$的一个$n$维子空间，$\alpha_1,\alpha_2,\cdots,\alpha_r$是$W$的一组基，那么这组向量必定可以扩充为整个空间的基。

也就是说，在$V$中必定可以找到$n-m$个向量$\alpha_{m+1},\alpha_{m+2},\cdots,\alpha_n$使得$\alpha_1,\alpha_2,\cdots,\alpha_n$是$V$的一组基。

子空间的运算——交与和

定理

如果$V_1,V_2$是线性空间$V$的两个子空间，那么它们的交$V_1\cap V_2$也是$V$的子空间。

由集合的交的定义可以看出，子空间的交适合以下运算律：
1. 交换律 $V_1 \cap V_2 =V_2 \cap V_1$
2. 结合律 $(V_1 \cap V_2)\cap V_3 =V_1\cap (V_2 \cap V_3)$
  
  由结合律我们可以定义多个子空间的交 $V_1 \cap V_2 \cap \cdots \cap V_s = \cap_{i=1}^sV_i$
定义子空间的和

$V_1,V_2$是线性空间$V$的两个子空间,所谓$V_1$与$V_2$的和，是指所有能够表示为$\alpha_1+\alpha_2$，而$\alpha_1 \in V_1,\alpha_2 \in V_2$的向量组成的子集合，记作$V_1+V_2$。$V_1+V_2=\{\alpha|\alpha=\alpha_1+\alpha_2,\alpha_1\in V_1,\alpha_2 \in V_2\}$

由定义可以看出，子空间的和适合以下运算律：
1. 交换律 $V_1 + V_2 =V_2 + V_1$
2. 结合律 $(V_1 + V_2)+ V_3 =V_1 + (V_2 + V_3)$
  
  由结合律我们可以定义多个子空间的交 $V_1 + V_2 + \cdots + V_s = \sum_{i=1}^sV_i$。
定理

如果$V_1,V_2$是线性空间$V$的两个子空间，那么它们的和$V_1 + V_2$也是$V$的子空间。

关于子空间的交与和有以下结论：

设$V_1,V_2,W$都是子空间，那么由$W \subset V_1 $与$W \subset V_2 $可以推出$W \subset V_2 \cap V_1 $；

由$W \supset V_1 $与$W \supset V_2 $可以推出$W \supset V_2 + V_1 $；
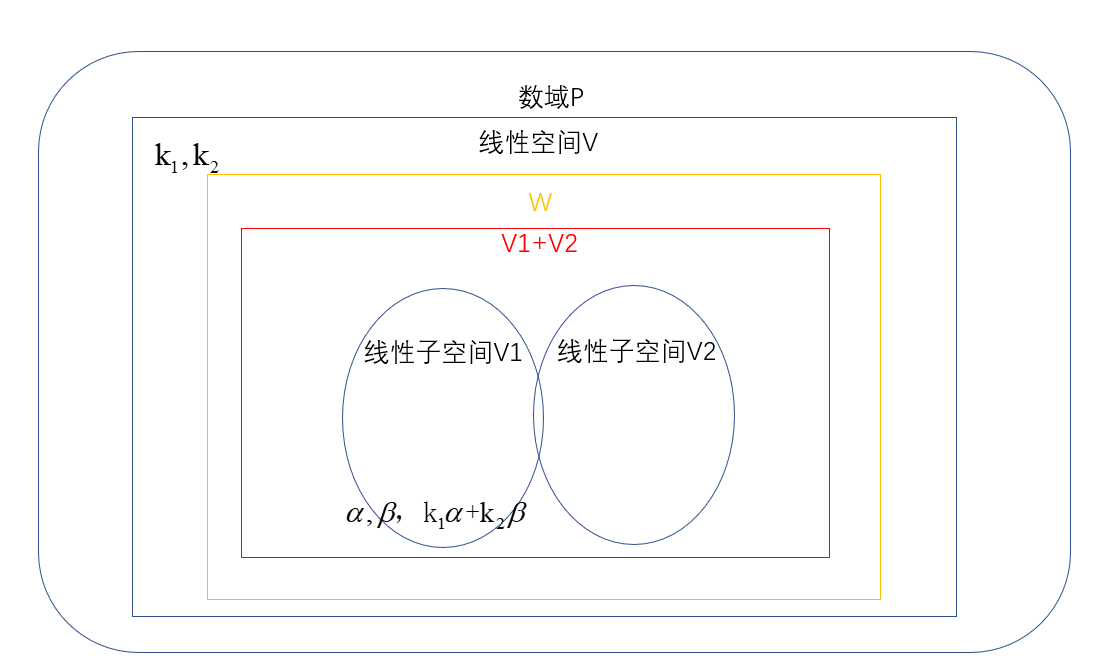
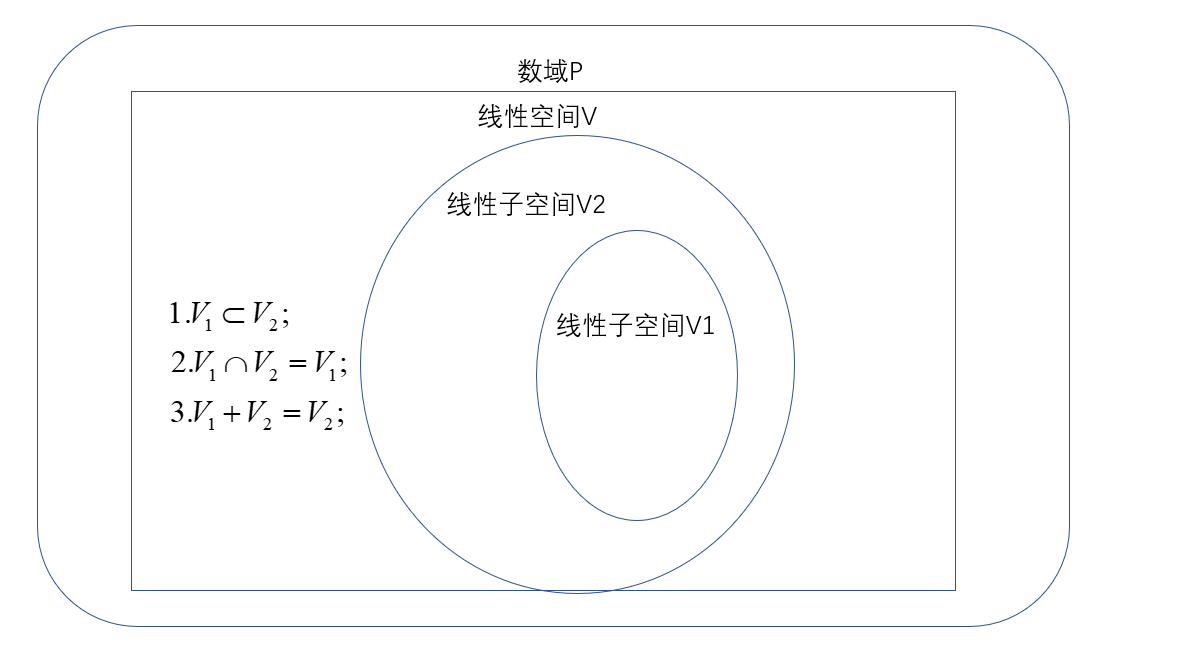
对于子空间$V_1$与$V_2$，以下三个论断是等价的：
- $V_1 \subset V_2$;
- $V_1 \cap V_2 =V_1$；
- $V_1+V_2=V_2$

例子

在三维几何空间中，用$V_1$表示一条通过原点的直线，$V_2$表示一张通过原点且与$V_1$垂直的平面，那么$V_1,V_2$的交是$\{0\}$，而$V_1,V_2$的和是整个空间。
在一个线性空间$V$中，我们有

\[L(\alpha_1,\alpha_2,\cdots,\alpha_s)+L(\beta_1,\beta_2,\cdots,\beta_t) \\ =L(\alpha_1,\alpha_2,\cdots,\alpha_s,\beta_1,\beta_2,\cdots,\beta_t) \]

定理维数定理

如果$V_1,V_2$是线性空间$V$的两个子空间，那么

  					维（$V_1$）+维（$V_2$） =维（$V_1+V_2$）+维（$V_1 \cap V_2$）

推论：如果$n$维线性空间$V$中两个子空间$V_1,V_2$的维数之和大于$n$，那么$V_1,V_2$必含有非零的公共向量。

子空间的直和

定义

设$V_1,V_2$是线性空间$V$的子空间，如果和$V_1+V_2$中每一个向量$\alpha$的分解式

\[\alpha=\alpha_1+\alpha_2 ,\ \ \alpha_1 \in V_1 ,\alpha_2 \in V_2 \]
是唯一的，这个和就称为直和，记为$V_1\oplus V_2$

例子1中子空间的和就是直和。
定理

和$V_1+V_2$是直和的充分必要条件是

等式 $\alpha_1+\alpha_2=0 ,\ \ \alpha_1 \in V_1 ,\alpha_2 \in V_2$只有在$a_1,a_2$全为零向量时才成立。
- 推论：和$V_1+V_2$为直和的充分必要条件是$V_1 \cap V_2=\{0\}$
定理

设$V_1,V_2$是线性空间$V$的子空间，令$W=V_1+V_2$，则$W=V_1\oplus V_2$的充分必要条件是

\[维(W)=维(V_1)+维(V_2) \]
互补子空间，补空间

定理

设$U$是线性空间$V$的一个子空间，那么一定存在一个子空间$W$，使$V=U\oplus W$。

$U$叫做$W$的补空间，$U$和$W$互为补子空间。

推广到多个子空间的情形

定义

设$V_1,V_2,\cdots,V_s$是线性空间$V$的子空间，如果和$V_1+V_2+\cdots+V_s$中每一个向量$\alpha$的分解式

\[\alpha=\alpha_1+\alpha_2+\cdots+\alpha_s ,\ \ \alpha_i \in V_i(i=1,2,\cdots,s) \]

是唯一的，这个和就称为直和，记为$V_1\oplus V_2 \oplus \cdots \oplus V_s$

定理设$V_1,V_2,\cdots,V_s$是线性空间$V$的子空间，下面这些条件是等价的
1. $W=\sum V_i$是直和；
2. 零向量的表法唯一；
3. $V_i \cap \sum_{j \neq i}{V_j}=\{0\}\ \ \ (i=1,2,\cdots,s)$；
4. 维($W$)=$\sum$维（$V_i$）

同构

向量在用坐标表示后，它们的运算就可以归结为它们坐标的运算。线性空间$V$的讨论可以归结于$P^n$的讨论。

定义

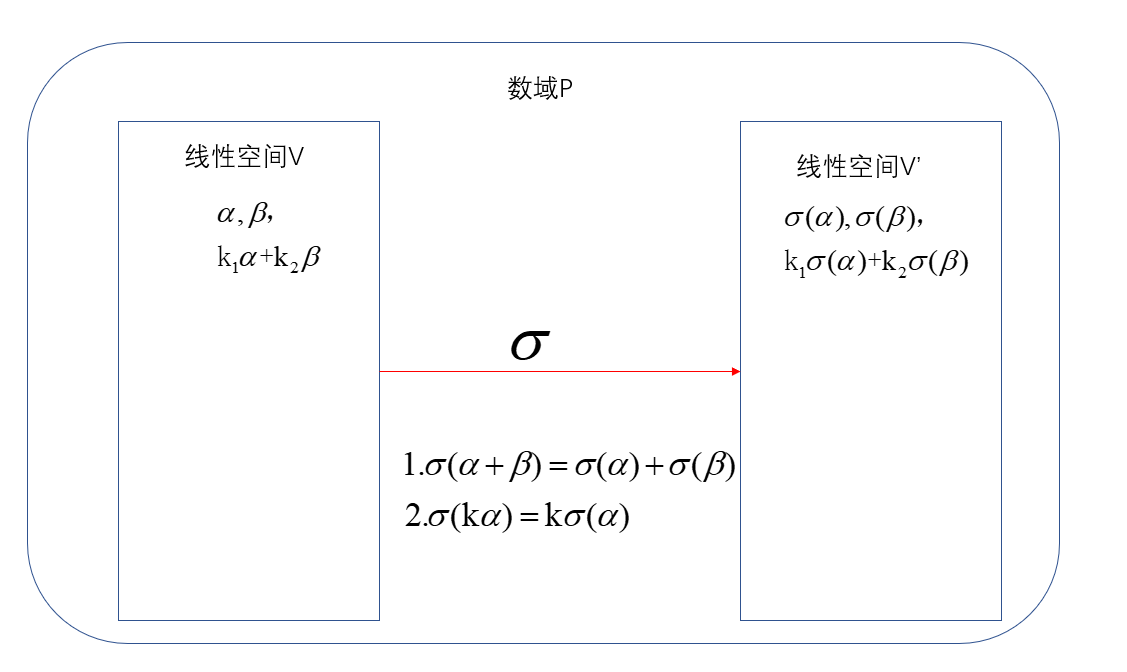
数域$P$上两个线性空间$V$与$V'$称为同构的，如果由$V$到$V'$有一个双射$\sigma$具有以下性质：

$\sigma(\alpha+\beta)=\sigma(\alpha)+\sigma(\beta)$；
$\sigma(k\alpha)=k\sigma(\alpha)$

其中$\alpha,\beta$是$V$中任意向量，$k$是$P$中任意数。

这样的映射$\sigma$称为同构映射。

基本性质

$\sigma(0)=0,\sigma(-\alpha)=-\sigma(\alpha)$。
$\sigma(k_1\alpha_1+k_2\alpha_2+\cdots+k_r\alpha_r)=k_1\sigma(\alpha_1)+k_2\sigma(\alpha_2)+\cdots+k_r\sigma(\alpha_r)$。
$V$中向量组$\alpha_1,\alpha_2,\cdots,\alpha_r$线性相关的充分必要条件是它们的像$\sigma(\alpha_1),\sigma(\alpha_2),\cdots,\sigma(\alpha_r)$线性相关。

同构的线性空间有相同的维数
如果$V_1$是$V$的一个子空间，那么$V_1$在$\sigma$下的像集合 $\sigma(V_1)=\{\sigma(\alpha)|\alpha \in V_1\}$是$\sigma(V)$的子空间，并且$V_1$与$\sigma(V_1)$维数相同。
同构映射的逆映射以及两个同构映射的乘积还是同构映射。

同构映射作为线性空间之间的关系，具有自反性，对称性，传递性。

数域$P$上任一个$n$维线性空间都与$P^n$同构。

数域$P$上任意两个$n$维线性空间都同构。

定理

数域$P$上两个有限线性空间同构的充分必要条件是它们有相同的维数。

维数是有限线性空间的唯一的本质特征。

标签：varepsilon,高等,空间,cdots,线性,alpha,代数,sigma
来源： https://www.cnblogs.com/zuti666/p/13580033.html