卡特兰数的英文维基讲得非常全面，强烈建议阅读！

Catalan number - Wikipedia

(本文中图片也来源于这个页面)
由于本人太菜，这里只选取其中两个公式进行总结。
（似乎就是这两个比较常用？）
首先先扔卡特兰数的定义式

Catalann=∑i=1n−1Catalani∗Catalann−i$$Catala{n}_n=\sum _{i=1}^{n-1}Catala{n}_i\ast Catala{n}_{n-i}$$

(卡特兰数的很多应用，比如二叉树形态数，出栈序列数等，都由这个定义式得到。详见英文维基)

公式1 (通项公式) ：

Catalann=1n+1Cn2n$$Catala{n}_n=\frac{1}{n+1}{C}_{2n}^n$$

在上文提到的出栈序列的问题情景中，如果有n$n$个元素，在平面直角坐标系中用x$x$坐标表示入栈数，y$y$坐标表示出栈数，则坐标(a,b)$(a,b)$表示目前已经进行了a$a$次入栈和b$b$次出栈，则再进行一次入栈就是走到(a+1,b)$(a+1,b)$，再进行一次出栈就是走到(a,b+1)$(a,b+1)$。并且，由于入栈数一定小于等于出栈数，所以路径不能跨越直线y=x$y=x$
因此，题目相当于求从(0,0)$(0,0)$走到(n,n)$(n,n)$且不跨越直线y=x$y=x$的方案数
首先，如果不考虑不能跨越直线y=x$y=x$的要求，相当于从2n$2n$次操作中选n$n$次进行入栈，则方案数为Cn2n$C_{2n}^n$。
然后，考虑对于一种不合法的方案，一定在若干次操作后有一次出栈数比入栈数多一次，这个点在直线y=x+1$y=x+1$ (即下图中红色的线) 上。那么把第一次碰到该直线以后的部分关于该直线对称，则最终到达的点是(n−1,n+1)$(n-1,n+1)$ (如下图) 。

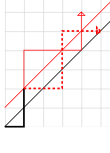
图源：英文维基 (即文首网址)
显然，任何非法方案都可以通过此方式变成一条从(0,0)$(0,0)$到(n−1,n+1)$(n-1,n+1)$的路径，有Cn+12n$C_{2n}^{n+1}$种。而任何合法方案由于不接触直线y=x+1$y=x+1$，无论从哪个点对称都不是一条连续的路径。由于合法方案数就是Catalann$Catala{n}_n$，所以：

Catalann=Cn2n−Cn+12n=(2n)!n!∗n!−(2n)!(n+1)!∗(n−1)!=1n+1((2n)!∗(n+1)n!∗n!−(2n)!n!∗(n−1)!)=1n+1((2n)!∗(n+1)n!∗n!−(2n)!∗nn!∗n!)=1n+1∗(2n)!∗(n+1)−(2n)!∗nn!∗n!=1n+1∗(2n)!n!∗n!=1n+1Cn2n$$\begin{array}{rl}Catala{n}_n& =C_{2n}^n-C_{2n}^{n+1}\\ & =\frac{(2n)!}{n!\ast n!}-\frac{(2n)!}{(n+1)!\ast (n-1)!}\\ & =\frac{1}{n+1}(\frac{(2n)!\ast (n+1)}{n!\ast n!}-\frac{(2n)!}{n!\ast (n-1)!})\\ & =\frac{1}{n+1}(\frac{(2n)!\ast (n+1)}{n!\ast n!}-\frac{(2n)!\ast n}{n!\ast n!})\\ & =\frac{1}{n+1}\ast \frac{(2n)!\ast (n+1)-(2n)!\ast n}{n!\ast n!}\\ & =\frac{1}{n+1}\ast \frac{(2n)!}{n!\ast n!}\\ & =\frac{1}{n+1}{C}_{2n}^n\end{array}$$

公式2 (递推公式) ：

Catalann+1=4n+2n+2Catalann$$Catala{n}_{n+1}=\frac{4n+2}{n+2}Catala{n}_n$$

(这个公式的推导过程似乎网上没有，估计是思路太简单了……我太菜了想了半天才推出来)
由上面那个通项公式得

Catalann+1=1n+2Cn+12n+2=1n+2∗(2n+2)!(n+1)!∗(n+1)!=1n+2∗(2n)!∗(2n+1)∗(2n+2)n!∗n!∗(n+1)2=1n+2∗(2n+1)∗(2n+2)(n+1)∗1n+1∗(2n)!n!∗n!=2(2n+1)n+2∗1n+1∗Cn2n=4n+2n+2Catalann$$\begin{array}{rl}Catala{n}_{n+1}& =\frac{1}{n+2}{C}_{2n+2}^{n+1}\\ & =\frac{1}{n+2}\ast \frac{(2n+2)!}{(n+1)!\ast (n+1)!}\\ & =\frac{1}{n+2}\ast \frac{(2n)!\ast (2n+1)\ast (2n+2)}{n!\ast n!\ast (n+1{)}^2}\\ & =\frac{1}{n+2}\ast \frac{(2n+1)\ast (2n+2)}{(n+1)}\ast \frac{1}{n+1}\ast \frac{(2n)!}{n!\ast n!}\\ & =\frac{2(2n+1)}{n+2}\ast \frac{1}{n+1}\ast C_{2n}^n\\ & =\frac{4n+2}{n+2}Catala{n}_n\end{array}$$

[转载自Inspector_Javert](https://www.cnblogs.com/zyt1253679098/p/9190217.html)

标签：直线,兰数,出栈,nn,卡塔,Catalann,2n,1n
来源： https://www.cnblogs.com/hnuzmh/p/16434816.html