3.3 系统的稳定性及其判据

3.3.1 在复平面上分析稳定性

由上一节的讨论发现，极点在OLHP中时，系统才会在足够长的时间后稳定在某一个值上。于是定义了稳定性：如果系统的传递函数\(G(s)\)的所有极点都在OLHP，那么说这个系统是稳定的。

• 系统是否稳定只与系统本身有关，而与输入无关。
• 在接下来的课程中还会遇到具有更加复杂含义的稳定性定义。

由之前的讨论，系统稳定要求极点都落在OLHP中，所以本章讨论的重点就是什么条件下一元高次方程的根的实部全部为负。因为4次以上的一元高次方程的解没有解析公式，所以本节的目的就在于找到一些间接的判断方法。

3.3.2 低阶系统的简单稳定性判断

• 方法一

  对于一、二阶系统，系统稳定的充要条件是分母多项式（即特征多项式）的所有系数均同号。

  对于更高阶的系统，系统稳定的必要条件是特征多项式的所有系数均同号（反证法，拆分成\(\prod(s-p_i)\)的形式）。

• 方法二

  \(n\)阶系统稳定的充要条件是：\(\omega\)从零增大到无穷大的过程中，\(\Delta\arg D(j\omega)=\frac{n\pi}{2}\)

• 方法三

  \(n\)阶系统稳定的充要条件：\(\omega\)从零增大到无穷大的过程中，\(D(j\omega)\)在复平面上的轨迹逆时针绕过原点\(n\)个四分之一圈。

• 方法四（Hermite-Bieler定理）

  将特征多项式\(D(j\omega)\)做如下拆分

  \[\begin{aligned} &D(j \omega)=h\left(\omega^{2}\right)+j \omega g\left(\omega^{2}\right)\\ &h(\lambda)=a_{0}-a_{2} \lambda+a_{4} \lambda^{2}-a_{6} \lambda^{3}+\cdots \\ &g(\lambda)=a_{1}-a_{3} \lambda+a_{5} \lambda^{2}-a_{7} \lambda^{3}+\cdots \end{aligned}\quad \text{with }\lambda=\omega^2 \]

  则\(n\)阶系统稳定的充要条件是：

  • \(a_i\)同号

  • 随着\(\omega\)从零增大到为无穷大，\(h(\lambda)\)和\(g(\lambda)\)轮流有解，即设它们的根分别为\(\lambda_{h,i}\)和\(\lambda_{g,i}\)，则

    \[0<\lambda_{h,1}<\lambda_{g,1}<\lambda_{h,2}<\lambda_{g,2}<\lambda_{h,3}<\lambda_{g,3}<\cdots \]

  ---

  • 对于三阶系统特征多项式\(a_3(j\omega)^3+a_2(j\omega)^2+a_1j\omega+a_0\)，由该法可以推知稳定的充要条件是

    \[\left\{ \begin{aligned} &a_1 a_2 − a_0 a_3 > 0\\ &a_i同号 \end{aligned} \right. \]

  • 不难发现，方法二到四基本说的是同一件事。方法四仍然需要求解\(h(\lambda)\)和\(g(\lambda)\)的根才能进行判断，所以其判断的范围最多只能到9阶系统。

3.3.3 劳斯判据

定理内容

• 劳斯矩阵的求法

  暂时略过，课上只讲了操作（本节的其他许多内容也是），没讲为什么，记成笔记没啥意义。。。考完试有时间再补上啦。

  注意劳斯矩阵是根据闭环传递函数的分母写的。

• 劳斯判据的叙述

  劳斯矩阵中第一列各项的负号变化次数，等于特征方程的实部大于0的根的个数。

  ---

  注意是“大于”。如果出现了实部为0的根

  • 在原点有根，则会没有常数项，易于判断。
  • 有关于原点对称的根，则劳斯矩阵中会出现全零行。

特殊情况处理

• 劳斯矩阵的第一列出现了0

  • 法一：求其互补多项式的劳斯矩阵，再判断其稳定性。

    • 原理：互补多项式定义为
      \[D_{\mathrm{rec}}(s) \triangleq s^{n} D\left(\frac{1}{s}\right)=a_{0} s^{n}+a_{1} s^{n-1}+\cdots+a_{n-1} s+a_{n} \]
      因为\(\frac{1}{s}\)和\(s\)具有相同的实部，故两者的稳定性判断结论应该一样。

  • 法二：求原多项式乘上一项新的\((s+p_i)\)后的劳斯矩阵，选取合适的\(p_i\)使得第一列中不再有0。因为\((s+p_i)\)的极点位置已知，所以将新的结果减去\((s+p_i)\)在右半平面的极点个数即可得到原多项式在右半平面的极点个数。

  • 法三：

• 有全0行：意味着有纯虚根

  将全零行的上一行对应的多项式写出，然后对其求导，用所得结果的系数替换掉全零行，然后继续进行劳斯矩阵的列写。

3.3.3 赫尔维茨稳定性判据

再次略，课上只简单地讲了讲结论。

3.3.4 确定系统参数的稳定范围

本节的基本思路就只是把系统参数当作未知数算出劳斯矩阵，然后在假设系统稳定的情况下求解这些参数的取值范围。

要注意的从这一节开始，讨论的对象都是开环传递函数\(G_o(s)\)，而本章此前讨论的都是闭环传递函数。

3.4 稳态响应分析

3.4.1 定义

• 稳态误差：\(e_{ss}\triangleq\lim\limits_{t\to\infty}[r(t)-y(t)]=\lim\limits_{t\to\infty}e(t)\)

• 系统型次

  \[G_o(s)=\frac{K_o(\tau_1s+1)(\tau_2s+1)\cdots(\tau_ms+1)}{s^l(T_1s+1)(T_2s+1)\cdots(T_ps+1)},\ l+p=n \]

  在这样的表示方式下，\(l\)就定义为系统的型次。本节主要介绍随着型次的提升，系统的稳态误差会减小。应该注意的是，型次越高系统的稳定性也会越差，需要在二者之间取舍。

3.4.2~3.4.6 单位反馈系统的稳态误差

通过终值定理求稳态误差

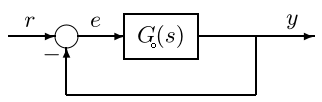
对于单位反馈系统有

\[\tilde e(s)=\tilde r(s)-G\tilde e(s)\Leftrightarrow\tilde e(s)=\frac{\tilde r(s)}{1+G_o(s)} \]

在拉普拉斯变换定义式中使用分部积分，有

\[\begin{aligned} \tilde e(s)&=\int_0^\infty e(t)e^{-st}{\mathrm d}t\\ &=\int_0^\infty e(t)\frac{\mathrm d}{\mathrm dt}(-\frac{1}{s}e^{-st}){\mathrm d}t\\ &=-\left.e(t)\frac{1}{s}e^{-st}\right|_0^\infty+\frac{1}{s}\int_0^\infty e'(t)e^{-st}{\mathrm d}t\\ &=\frac{1}{s}e(0)+\frac{1}{s}\int_0^\infty e'(t)e^{-st}{\mathrm d}t\\ \Rightarrow \lim\limits_{s\to0}s\tilde e(s)&=e(0)+\lim\limits_{t\to\infty}e(t)-e(0)=\lim\limits_{t\to\infty}e(t)\\ \lim\limits_{t\to\infty}e(t)&= \lim\limits_{s\to0}s\tilde e(s) \end{aligned} \]

故稳态误差的一种求解方法为

\[e_{ss}=\lim\limits_{t\to\infty}e(t)=\lim\limits_{s\to0}\frac{s\tilde r(s)}{1+G_o(s)} \]

阶跃、斜坡、抛物线输入下的稳态误差

三个误差还分别对应称为稳态位置、速度、加速度误差。

运用由终值定理求得的结论，易得0~2型次系统的这些误差

型次	稳态位置误差	稳态速度误差	稳态加速度误差
0	\(\frac{1}{1+K_o}\)	\(\infty\)	\(\infty\)
1	0	\(\frac{1}{K_o}\)	\(\infty\)
2	0	0	\(\frac{1}{K_o}\)

可以发现随着型次的增加，稳态误差减小。

正弦输入的稳态误差

正弦输入的稳态误差可以通过在前馈通路（feed forward path）增加\(\frac{\omega}{s^2+\omega^2}\)环节而保证消除，因为

\[e_{ss} =\lim\limits_{s\to0}\frac{s\frac{\omega}{s^2+\omega^2}}{1+\frac{\omega}{s^2+\omega^2}G_o(s)}=\lim\limits_{s\to0}\frac{s\omega}{s^2+\omega^2+\omega G_o(s)}=0 \]

3.4.7 无稳态误差时非单位反馈系统反馈回路增益的作用

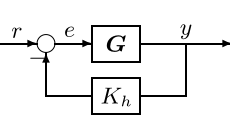
无稳态误差时，有关系

\[r(t)-K_hy(\infty)=0\\ \Rightarrow y(\infty)=\frac{r(\infty)}{K_h} \]

所以调节\(K_h\)，可以改变\(y(\infty)\)的大小。

3.4.8 含扰动系统的稳态误差

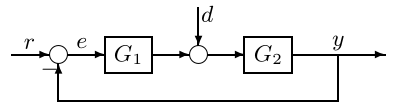
因为目前为止讨论的都是线性系统，所以可以设输入\(r\)为0，单独考虑扰动\(d\)的作用。运用拉普拉斯变换的终值定理也可以求出系统关于\(d\)的稳态误差。

标签：误差,frac,infty,稳态,自控,omega,lambda
来源： https://www.cnblogs.com/harold-lu/p/15729565.html