本文转自【https://mathworld.wolfram.com/Point-LineDistance3-Dimensional.html】

Point-Line Distance--3-Dimensional

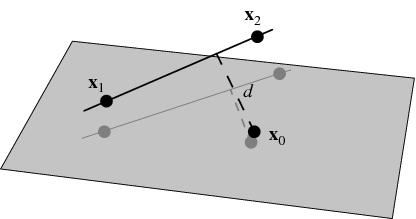
Let a line in three dimensions be specified by two points  and  lying on it, so a vector along the line is given by

(1)

The squared distance between a point on the line with parameter  and a point  is therefore

(2)

To minimize the distance, set  and solve for  to obtain

(3)

where  denotes the dot product. The minimum distance can then be found by plugging  back into (2) to obtain

	(4)
	(5)
	(6)

Using the vector quadruple product

(7)

where  denotes the cross product then gives

(8)

and taking the square root results in the beautiful formula

			(9)
			(10)
			(11)

Here, the numerator is simply twice the area of the triangle formed by points , , and , and the denominator is the length of one of the bases of the triangle, which follows since, from the usual triangle area formula, 

 

Matlab代码实现

norm是计算范数，默认是计算模。

p1= [1,2,3];
p2=[2,3,8];
p0=[4,5,6];
dis = norm(cross((p0-p1),(p0-p2)))/norm(p2-p1);

标签：p2,直线,product,triangle,distance,三维空间,点到,line,norm
来源： https://www.cnblogs.com/elapsetor/p/14668707.html