浅谈整除分块(复习)
作者:互联网
复习整除分块
经典例子:
求Σ(n/i),n<=1e14,()为向下取整
考虑直接暴力肯定不行,但发现其中有很多数是一样的
引进整除分块:
右端点为n/(n/l):表示n/l的值n中有多少个
左端点为上一个r+1
复杂度为根号n
code:
inline void init (int ans=0) {
for(int l=1,r,len;l<=n;l=r+1) {
r=n/(n/l),len=r-l+1;
ans+=len*(n/l);
}
}当然整除分块不仅仅只能处理这种形式
它是一种思想,一种美妙的剪枝
应用:
例题一:
https://www.luogu.org/problem/P3935
给定两个数L,R(L<=R<=1e9),求[L,R]中每个元素的约数个数和
分析:
首先很明显一个前缀和,剩下的问题成了求[1,X]中每个元素的约数个数和
暴力不行,就只有分别考虑每个约数出现的次数了
考虑[1,X]中以i为倍数的有X/i个
所以答案就成了Σn/i
code by wzxbeliever:
#include<bits/stdc++.h>
#define ll long long
#define il inline
#define ri register int
#define lowbit(x) x&(-x)
using namespace std;
const int mod=998244353;
ll l,r;
il ll solve(ll x){
ll ans=0;
for(register ll i=1,j;i<=x;i=j+1){
j=x/(x/i);
ans+=(j-i+1)*(x/i)%mod;
}
return ans;
}
int main(){
scanf("%lld%lld",&l,&r);
printf("%lld\n",(solve(r)-solve(l-1)+mod)%mod);
return 0;
}
插入一个复习块(和本题无关):

例题二:
https://www.luogu.org/problem/P2261
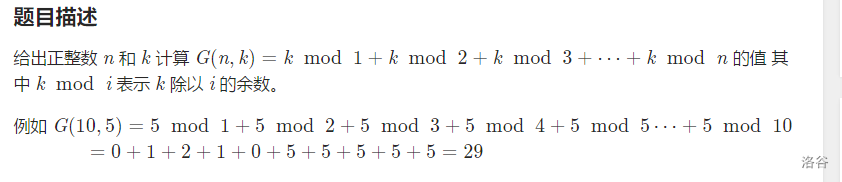
分析:

code:
#include<cstdio>
#include<algorithm>
using namespace std;
typedef long long ll;
int main() {
ll n,k;
scanf("%lld%lld",&n,&k);
ll ans=n*k;
for(ll l=1,r;l<=n;l=r+1) {
if(k/l) r=min(k/(k/l),n);
else r=n;
ans-=(k/l)*(r-l+1)*(l+r)/2;
}
printf("%lld",ans);
return 0;
}例题三:

分析:
分别算出(Nmodi)和(Mmodj)
再将两者相乘
即为答案
例题四:

吐槽:
心路历程:1.考虑每段的贡献,但是要处理每个K,不现实
2.考虑先不看节点,再找到一些规律,做一些变换得答案,但是貌似没啥规律结论
分析:
同样发现有很多的K的值不同,但得出的答案是一样的
考虑整除分块
将询问离线成三个点的询问,每个询问都是形如求f(u,1,w)的值。
考虑每条边的贡献,整除分块后每次相当于将子树内每个点的f(u,1,l)~f(u,1,r)都加上一个值。
于是我们最后再 dfs 一遍,经过一条边的时候,将这条边的边权整除分块,并在树状数组的对应区间上 修改,退出的时候再将该边的影响去除。遍历到某个点查询的时候,直接查询树状数组某个点的值即 可
code by std:
#include <bits/stdc++.h>
template <class T>
inline void read(T &x)
{
static char ch;
while (!isdigit(ch = getchar()));
x = ch - '0';
while (isdigit(ch = getchar()))
x = x * 10 + ch - '0';
}
template <class T>
inline void putint(T x)
{
static char buf[25], *tail = buf;
if (!x)
putchar('0');
else
{
for (; x; x /= 10) *++tail = x % 10 + '0';
for (; tail != buf; --tail) putchar(*tail);
}
}
typedef long long s64;
const int MaxNV = 1e5 + 5;
const int MaxNE = MaxNV << 1;
const int MaxLog = 18;
struct request
{
int d, opt, pos;
request(){}
request(int y, int z, int p):
d(y), opt(z), pos(p) {}
};
int n, m = 30000, Q;
s64 bit[MaxNV], ans[MaxNV];
std::vector<int> add[MaxNV];
std::vector<request> req[MaxNV];
int ect, adj[MaxNV];
int to[MaxNE], e_w[MaxNE], nxt[MaxNE];
int dep[MaxNV];
int anc[MaxNV][MaxLog + 1];
#define trav(u) for (int e = adj[u], v, w; v = to[e], w = e_w[e], e; e = nxt[e])
inline void addEdge(int u, int v, int w)
{
nxt[++ect] = adj[u];
adj[u] = ect;
e_w[ect] = w;
to[ect] = v;
}
inline void bit_modify(int x, int del)
{
for (; x <= m; x += x & -x)
bit[x] += del;
}
inline s64 bit_query(int x)
{
s64 res = 0;
for (; x; x ^= x & -x)
res += bit[x];
return res;
}
inline int query_lca(int u, int v)
{
if (dep[u] < dep[v])
std::swap(u, v);
for (int i = 0, d = dep[u] - dep[v]; d; d >>= 1, ++i)
if (d & 1)
u = anc[u][i];
if (u == v)
return u;
for (int i = MaxLog; i >= 0; --i)
if (anc[u][i] != anc[v][i])
{
u = anc[u][i];
v = anc[v][i];
}
return anc[u][0];
}
inline void dfs_init(int u)
{
for (int i = 0; anc[u][i]; ++i)
anc[u][i + 1] = anc[anc[u][i]][i];
trav(u) if (v != anc[u][0])
{
anc[v][0] = u;
dep[v] = dep[u] + 1;
dfs_init(v);
}
}
inline void modify(int x, int opt)
{
int lst = 0, lst_del = 0; --x;
for (int cur = 1; cur <= x; cur = lst + 1)
{
lst = x / (x / cur);
bit_modify(cur, +opt * (x / cur + 1) - lst_del);
lst_del = opt * (x / cur + 1);
}
bit_modify(x + 1, opt - lst_del);
}
inline void dfs_answer(int u)
{
int cnt_req = req[u].size();
for (int j = 0; j < cnt_req; ++j)
{
int d = req[u][j].d, opt = req[u][j].opt;
ans[req[u][j].pos] += bit_query(d) * opt;
}
trav(u) if (v != anc[u][0])
{
modify(w, +1);
dfs_answer(v);
modify(w, -1);
}
}
int main()
{
freopen("delivery.in", "r", stdin);
freopen("delivery.out", "w", stdout);
read(n), read(Q);
for (int i = 1; i < n; ++i)
{
int u, v, w;
read(u), read(v), read(w);
addEdge(u, v, w), addEdge(v, u, w);
}
dfs_init(1);
for (int i = 1; i <= Q; ++i)
{
int u, v, w, z;
read(u), read(v), read(w);
z = query_lca(u, v);
ans[i] = 1;
req[u].push_back(request(w, +1, i));
req[v].push_back(request(w, +1, i));
req[z].push_back(request(w, -2, i));
}
dfs_answer(1);
for (int i = 1; i <= Q; ++i)
putint(ans[i]), putchar('\n');
return 0;
}其实也可以平衡规划
这一个阙值K,小于k的暴力预处理,大于k的主席树
code by hs:
#include<bits/stdc++.h>
using namespace std;
#define maxn 100010
#define maxm 210
template<typename T>T read()
{
T res=0;
int sym=1;
char cc=getchar();
while(!isdigit(cc)&&cc!='-')
cc=getchar();
if(cc=='-')sym=-1,cc=getchar();
while(!isdigit(cc))cc=getchar();
while(isdigit(cc))res=res*10+cc-'0',cc=getchar();
return sym*res;
}
template<typename T>void read(T &o)
{
o=read<T>();
}
template<typename A,typename... B>void read(A& o,B&... Others)
{
o=read<A>();
read(Others...);
}
struct Edge
{
int v;
int w;
Edge *next;
Edge(int a=0,int b=0,Edge *c=NULL)
{
v=a;
w=b;
next=c;
}
}*head[maxn];
struct Node
{
int v;
int l;
int r;
}node[maxn*50];
int n,m,mx,cnt,T[maxn],dep[maxn],vis[maxm],fa[maxn][19];
long long tot[maxm][maxn];
void insert(int &a,int b,int l,int r,int x)
{
a=++cnt;
node[a]=node[b];
node[a].v+=1;
if(l==r)return ;
int mid=(l+r)>>1;
if(x<=mid)insert(node[a].l,node[b].l,l,mid,x);
else insert(node[a].r,node[b].r,mid+1,r,x);
}
int query(int a,int b,int c,int l,int r,int x,int y)
{
if(l>=x&&r<=y)
return node[a].v+node[b].v-2*node[c].v;
int mid=(l+r)>>1,ans=0;
if(x<=mid)
ans+=query(node[a].l,node[b].l,node[c].l,l,mid,x,y);
if(y>mid)
ans+=query(node[a].r,node[b].r,node[c].r,mid+1,r,x,y);
return ans;
}
void dfs(int k)
{
dep[k]=dep[fa[k][0]]+1;
for(int i=1;i<=18;i++)
fa[k][i]=fa[fa[k][i-1]][i-1];
for(Edge *i=head[k];i!=NULL;i=i->next)
{
if(i->v==fa[k][0])
continue;
fa[i->v][0]=k;
insert(T[i->v],T[k],1,mx,i->w);
dfs(i->v);
}
}
void dfs2(int k,int t)
{
for(Edge *i=head[k];i!=NULL;i=i->next)
{
if(i->v==fa[k][0])
continue;
tot[t][i->v]=tot[t][k]+(i->w-1)/t;
dfs2(i->v,t);
}
}
int lca(int x,int y)
{
if(dep[x]<dep[y])
swap(x,y);
int d=dep[x]-dep[y];
for(int i=0;i<=18;i++)
if(d&(1<<i))
x=fa[x][i];
if(x==y)return x;
for(int i=18;i>=0;i--)
if(fa[x][i]!=fa[y][i])
x=fa[x][i],y=fa[y][i];
return fa[x][0];
}
int main()
{
freopen("delivery.in","r",stdin);
freopen("delivery.out","w",stdout);
read(n,m);
for(int i=1;i<n;i++)
{
int x,y,z;
read(x,y,z);
mx=max(mx,z);
head[x]=new Edge(y,z,head[x]);
head[y]=new Edge(x,z,head[y]);
}
dfs(1);
for(int i=1;i<=m;i++)
{
int x,y,z;
read(x,y,z);
if(x==y)
{
puts("1");
continue;
}
int l=lca(x,y);
if(z<=200)
{
if(!vis[z])
{
dfs2(1,z);
vis[z]=true;
}
printf("%lld\n",dep[x]+dep[y]-dep[l]-dep[fa[l][0]]+
tot[z][x]+tot[z][y]-tot[z][l]*2);
continue;
}
int ans=0;
for(int j=2;(j-1)*z+1<=mx;j++)
{
ans+=(j-1)*
query(T[x],T[y],T[l],1,mx,(j-1)*z+1,min(mx,j*z));
}
printf("%d\n",ans+dep[x]+dep[y]-dep[l]-dep[fa[l][0]]);
}
return 0;
}标签:浅谈,anc,int,ll,分块,cc,fa,整除,void 来源: https://www.cnblogs.com/wzxbeliever/p/11789027.html