PI参数的计算之二—— 应配置成什么样的系统
作者:互联网
参考 https://zhuanlan.zhihu.com/p/26587675
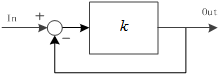
因为闭环传递函数比较复杂,特点不鲜明,同时所有的控制都是负反馈,所以只要开环传递函数确定了,闭环传递函数的特性也唯一了。
1、开环传递函数的几个特征
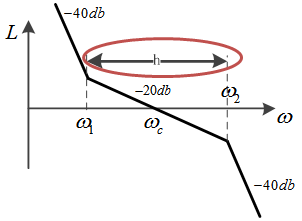
低频增益就是频率接近0时(直流分量),幅频特性的纵坐标值,如下图的蓝色圈所示。
这个值决定了闭环系统的稳态精度。
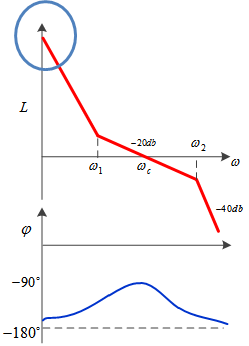
加入某开环传递函数的低频增益为K,那么闭环后,输出值只有输入值的K/(1+K),该值小于1,存在稳态误差。
只有当低频增益K为无穷大时,闭环增益才为1,消除了稳态误差。
所以,对于低频增益,我们希望越大越好,最好是无穷大。大家所熟知的积分环节,低频增益就是无穷大,用于消除稳态误差的。
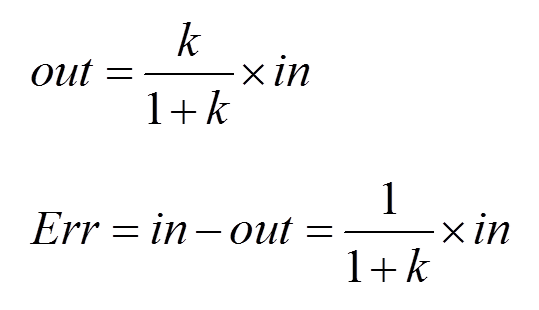
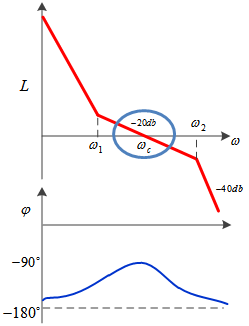
2. 高频增益就是频率比较高的增益,如下图蓝框所示。这一段增益决定了系统抗干扰的能力。
干扰,大部分都是什么脉冲、白噪声、扰动之类,都含有高频成分。
开环传递函数对高频的增益越低,衰减就越大,就不会对系统造成太大的扰动。
所以我们希望高频段能快速降到0db一下,斜率越陡越好。

1.3 带宽
带宽就是开环幅频特性过0db所对应的频率Wc,也叫截止频率,如下图蓝框所示。截止频率越高,代表系统响应速度越快。
截止频率以下,增益大于1,截止频率以上,增益小于1。
也就是说,截止频率越高,系统能响应的信号频率也就越高,当然响应速度也就越快了。
1.4 相角裕度
相角裕度,就是在截止频率处,相频特性对应的相角和-180度之间的举例,如下图所示。相角裕度决定了系统的稳定性。该值越大,系统越稳定。
-180度是不稳定的点,这是因为-180度就相当于反向,乘以了-1,就把本身的负反馈变成了正反馈,系统就失稳了。
-180度就是一个悬崖,在离悬崖越远的地方蹦腾,就越安全。
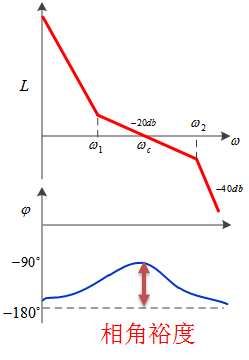
追求的是更高的稳态精度(低频增益)、更快的响应速度(截止频率)、更强的抗干扰能力(高频增益)和更稳定(相角裕度)。当然,这些目标是会互相矛盾的,鱼和熊掌不能兼得。
2 常用的开环传递函数
n型系统。
对于开环传递函数,分母中有r个s,就是r型系统。
0型系统,分母中没有s,低频增益是一个有限值,会有稳态误差。
3型及以上系统很难稳定,因为分母的一个s就是90度响应,多个s相角裕度很快就没有了。
所以常用的就是I型和II型系统。
![]()
2.1 I型系统
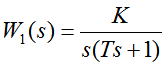
I型系统结构简单,1+Ts为系统本身的一阶惯性环节,只需要确定K值即可。该系统的缺点是,对斜坡和加速输入跟踪性能差。

从bode图上看,I型系统低频增益无穷大,没有稳态误差。高频以-40db斜率衰减,抗干扰能力强。截止频率越高,相角裕度越小;截止频率越低,相角裕度越大。
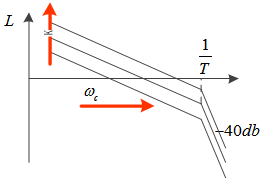
随着K增大,截止频率增大,增加了快速性;但降低了相角裕度和抗扰性。
在配置中,通常取KT=0.5,来权衡快速性和稳定性。
2.2 II型系统
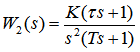
II型系统需要确定分子的两个参数K和τ,分母的1+Ts为系统的一阶惯性环节。II型系统对斜坡和加速输入能无静差跟踪。是电力电子控制中最常用的。
K和τ有众多种组合,怎么来合理的确定它们呢?
前人们针对II型系统有个中频带宽的概念,
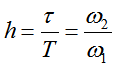
确定了中频宽h,就确定了τ,再改变K使得幅频特性上下平移,改变ωc。
学者们发现,对于确定的h,存在一个确定的K,使得闭环幅频特性峰值最小。
K和h的关系为
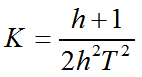
所以我们的工作就剩下,选择合适的h就可以了。
不同的h有什么影响呢?
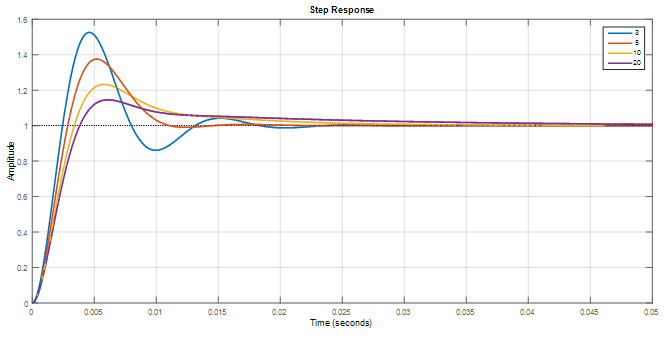
如下图所示,h越小,阶跃响应越快,但震荡越多,超调越大;
h越大,阶跃响应越慢,但震荡越小,超调越小。大家可以根据自己的需要,选择不同的h来配置II型系统。
下一篇,接着讲讲怎么将I和II型系统,应用到实际的PI参数配置中。
标签:什么样,截止频率,之二,II,增益,系统,相角,PI,传递函数 来源: https://www.cnblogs.com/realyuan2022/p/16449926.html