相似变换与相似矩阵

基底不同，向量的坐标值就不同 。对于同一个向量，选取的基底不同，其所对应的坐标值就不同。

例如：

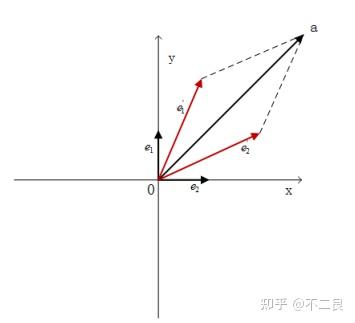
向量 \(a\) 在空间中的位置是固定的，如果使用第一组基底 \((e_1,e_2)=(\begin{bmatrix}1\\0 \end{bmatrix},\begin{bmatrix}0\\1 \end{bmatrix})\)。

向量 \(a\) 表示为 \(3\begin{bmatrix}1\\0 \end{bmatrix}+3\begin{bmatrix}0\\1 \end{bmatrix}\) ，那么在此基底下，向量 \(a\) 的坐标为 \(\begin{bmatrix}3\\3\end{bmatrix}\) 。

如果基底换为 \((e_1',e_2')=1\begin{bmatrix}2\\1 \end{bmatrix}+1\begin{bmatrix}1\\2 \end{bmatrix}\) 下，其坐标为 \(\begin{bmatrix}1\\1\end{bmatrix}\) 。

描述线性变换的矩阵也取决于基底 基底不同，描述向量线性变换的矩阵也不同 。

对于动态的向量变换，如向量从某个空间中的 位置 \(P\) 移动到 位置 \(Q\)，可以用矩阵来表示向量空间位置的改变，如果选取的基底不同，同一个运动在不同基底下，显然对应的矩阵表示也是不同的。

例如：

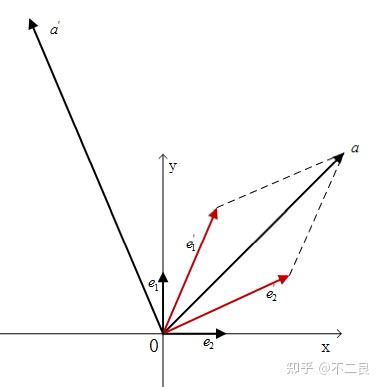
在这个二维空间中，向量从 \(a\) 变换到 \(a'\)。在基底 \((\begin{bmatrix}1\\0 \end{bmatrix},\begin{bmatrix}0\\1 \end{bmatrix})\) 的描述下，其坐标从 \(\begin{bmatrix}3\\3\end{bmatrix}\) 变换到 \(\begin{bmatrix}-3\\6\end{bmatrix}\) ，对应于这个线性变换的矩阵为 \(\begin{bmatrix}1&-2\\1 &1\end{bmatrix}\) 。

但是如果是在基底 \((\begin{bmatrix}2\\1 \end{bmatrix},\begin{bmatrix}1\\2 \end{bmatrix})\) 的描述下，其坐标的转换变成了 \(\begin{bmatrix}1\\1\end{bmatrix}\to \begin{bmatrix}-4\\5\end{bmatrix}\) 。

显然前一个基底下的变换矩阵就无法表示这个基底下的变换了。因为 \(\begin{bmatrix}1&-2\\1 &1\end{bmatrix}\times \begin{bmatrix}1\\1\end{bmatrix}\neq \begin{bmatrix}-4\\5\end{bmatrix}\) 。

相似矩阵与相似变换

针对指定向量的 同一个空间变换，用来 在不同基底下进行描述 的 不同矩阵，彼此之间称之为相似矩阵。相似矩阵所表示的线性变换，彼此之间称之为相似变换。

标签：begin,end,相似,变换,相似矩阵,bmatrix,基底,向量
来源： https://www.cnblogs.com/A-Quark/p/16439258.html