AcWing 122 糖果传递

题目传送门

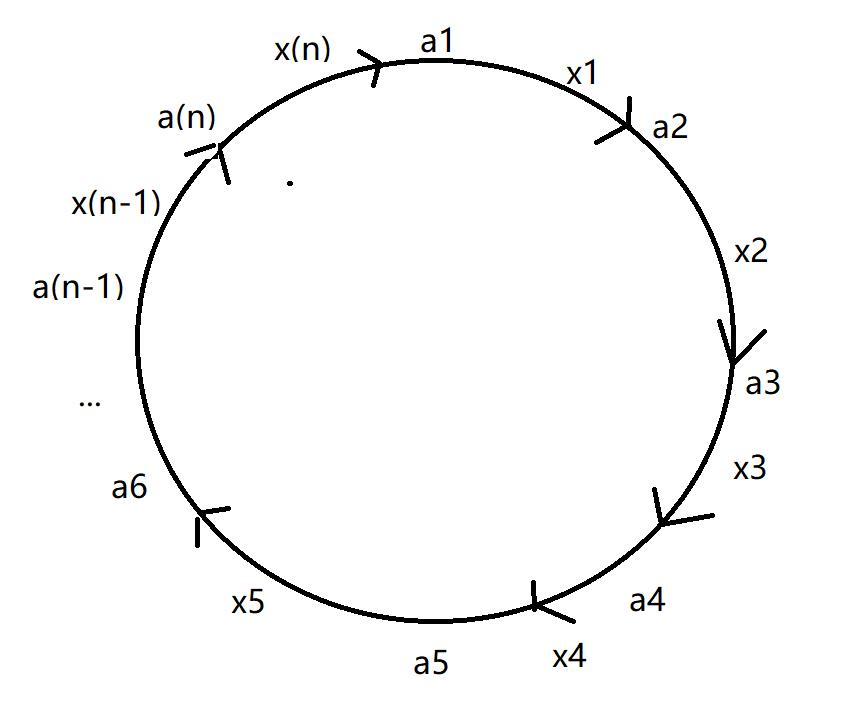
• 假设第\(1\)个小朋友有\(a_1\)颗糖果，给第\(2\)个小朋友\(x_1\)颗糖果，从\(n\)获得\(x_n\)颗糖果，此时，他有\(a_1-x_1+x_n\)颗糖果，同理，第\(2\)个有\(a_2-x_2+x_1\)，第\(3\)有...

• 每个小朋友的目标为平均数\(avg\),列出约束方程为

  \[\large \left\{\begin{matrix} a_1-x_1+x_n=avg & \\ a_2-x_2+x_1=avg & \\ a_3-x_3+x_2=avg & \\ ... \\ a_n-x_n+x_{n-1}=avg \end{matrix}\right. \]

  我们的目标：
  

  \[\large min(|x_1|+|x_2|+...+|x_n|) \]

下面，我们用\(x_n\)来表示上面的方程组：替代\(x_1,x_2,...,x_{n-1}\)

\[\large \left\{\begin{array}{l} x_1=a_1+x_n-avg \\ x_2=a_2+x_1-avg =(a_1+a_2)-2*avg-x_n & \\ x_3=a_3+x_2-avg =(a_1+a_2+a_3)-3*avg-x_n & \\ ... \\ x_{n-1}=(a_1+a_2+...+a_{n-1})-(n-1)*avg-x_n & \\ \end{array}\right. \]

将\(x_k\)定为变量 , 常数定义为\(c_k\)，则：

\[\large \displaystyle c_k=\sum_{i=1}^{k} -k*avg \]

有：

\[\large \left\{\begin{array}{l} x_1=c_1-x_n \\ x_2=c_2-x_n \\ ... \\ x_{n-1}=c_{n-1}-x_n \end{array}\right. \]

此时，我们的目标也就转化为:

$$
min(|c_1-x_n|+|c_2-x_n|+...+|c_{n-1}-x_n|)

\[</b></font> 注意到$|c_i-x_n|$的几何意义是数轴上的点$c_i$到$x_n$的距离，所以问题变成了：给定数轴上的$n$个点，找出一个到他们的距离之和尽量小的点，而这个点就是这些数中的中位数,问题再次转化为经典问题： [$104$.仓库选址](https://www.acwing.com/problem/content/106/) ，只需要求中位数和其他数的差值的总和就可以了。 ```c++ #include <bits/stdc++.h> using namespace std; const int N = 1000010; typedef long long LL; LL a[N], c[N], sum, avg, n, res; int main() { cin >> n; for (int i = 1; i <= n; i++) scanf("%lld", &a[i]), sum += a[i]; avg = sum / n; for (int i = 1; i <= n; i++) c[i] = c[i - 1] + a[i] - avg; sort(c + 1, c + n + 1); for (int i = 1; i <= n; i++) res += abs(c[i] - c[(n + 1) / 2]); printf("%lld\n", res); return 0; } ```\]

标签：...,right,large,122,array,avg,糖果,AcWing
来源： https://www.cnblogs.com/littlehb/p/16437042.html