标签:bold 平面 基础知识 计算 几何 theta times 向量 2y
计算几何基础知识
向量,极坐标
基础概念高中课本应该讲了吧 贴下 oiwiki 链接:向量,极坐标
平面向量在计算几何中一般用坐标来描述,\((x,y)\) 表示的是起点在 \((0,0)\),而终点在 \((x,y)\) 的平面向量。
所以我们也可以用点来描述向量。
理解下文的式子最好都将向量看成起点在 \((0,0)\),终点在 \((x,y)\) 的一个”箭头“。
基本运算:
设 \(\bold A (x_1,y_1)\),\(\bold B(x_2,y_2)\) 。
那么有:
\(\bold A+\bold B=(x_1+x_2,y_1+y2)\)。
\(\bold A-\bold B=(x_1-x_2,y_1-y_2)\)。
所以点的加减法可以理解成其表示向量的加减法。
而加减法的结果都是向量。
如果\(\bold A,\bold B\) 的夹角为 \(\theta\) 。那么有:
\(\bold A \cdot \bold B=|\bold A||\bold B|\cos\theta\)。
我们称其为 \(\bold A,\bold B\) 的点积。
以上我们的向量的运算都是在二维平面意义下的。
而在三维空间中我们有空间向量。也就是三维空间下的向量,类似平面向量,我们同样可以用一个点的坐标来描述空间向量。
设 \(\bold A(x_1,y_1,z_1),\bold B(x_2,y_2,z_2)\)。而上述二维平面下的运算,我们可以看成是空间向量 \(\bold A,\bold B\) 在 \(z\) 值相等时的运算。
定义向量 \(\bold A,\bold B\) 的向量积为 \(\bold A\times \bold B\)。其结果是一个向量。
这个玩意儿在平面上的应用就是用来判断两个向量的关系位置。
因为 \(\bold A\times \bold B =(y_1z_2-y_2z_1,z_1x_2-z_2x_1,x_1y_2-x_2y_1)\)。
设 \(\bold A,\bold B\) 之间的夹角为 \(\theta(\theta<\pi)\) ,且他们的 \(z\) 均为 \(0\)。
那么 \(\bold A\times \bold B=(0,0,x_1y_2-x_2y_1)\)。
易知向量积的方向由 \(x_1y_2-x_2y_1\) 决定。又根据右手定则(用来看向量积方向的),我们可以得出结论:
如果 \(x_1y_2-x_2y_1>0\)
那么 \(\bold B\) 就由 \(\bold A\) 在 \((x,y,0)(x\in \R,y\in \R)\) 平面内顺时针旋转 \(\theta\) 度得到。
反之,\(\bold B\) 就由 \(\bold A\) 在 \((x,y,0)(x\in \R,y\in \R)\) 平面内逆时针旋转 \(\theta\) 度得到。
\(x_1y_2-x_2y_1=0\) 时他俩重合奥。
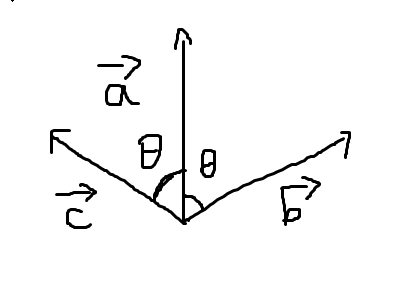
就像这样
\(\bold A\times\bold C>0,\bold A\times\bold B<0\)
极角排序
建立极坐标系,以 \(O\) 为极点,\(Ox\) 为极轴 ,正方向定义为逆时针方向。
设 $ (x,y)$ 为一个点 \(A\) (看做一个向量也行),那么这个点的极角是 \(\angle xOA\)。
一种做法是直接利用 \(atan2\) 函数求出极角进行排序,不过运算结果是 double,只能说懂得都懂。
还有一种做法就是先求出极角终边在哪个象限,然后利用叉乘求解。
划成四个象限似乎有些麻烦。
因为叉乘的应用范围是 \([0,\pi)\)。所以我们只要将一个平面划为两部分。如果两个点落在同一部分,那么利用叉乘求解,落在不同部分我们就根据自己定义来直接判断即可。
举个例子,如果我们要让 第四象限的角 \(<\) 第一象限的角 \(<\) 第二 \(<\) 第三。
那么我们将 \([-x,x)\) 划为第一部分,(\(x\) 代表 \(x\) 半轴,\(-x\) 就是负半轴),另一块是第二部分,如果两个点落在第一部分,那么用叉乘计算,如果 \(\bold A\times \bold B>0\) ,那么 \(\bold A\) 的极角小于 \(\bold B\) 的极角。
如果落在不同部分,根据我们的定义,第一部分的就小于第二部分。
凸包
这一块 oiwiki 讲的很详细了,我偷个懒。凸包。
闵可夫斯基和
看我写的这篇:
标签:bold,平面,基础知识,计算,几何,theta,times,向量,2y
来源: https://www.cnblogs.com/nightsky05/p/16211639.html
本站声明:
1. iCode9 技术分享网(下文简称本站)提供的所有内容,仅供技术学习、探讨和分享;
2. 关于本站的所有留言、评论、转载及引用,纯属内容发起人的个人观点,与本站观点和立场无关;
3. 关于本站的所有言论和文字,纯属内容发起人的个人观点,与本站观点和立场无关;
4. 本站文章均是网友提供,不完全保证技术分享内容的完整性、准确性、时效性、风险性和版权归属;如您发现该文章侵犯了您的权益,可联系我们第一时间进行删除;
5. 本站为非盈利性的个人网站,所有内容不会用来进行牟利,也不会利用任何形式的广告来间接获益,纯粹是为了广大技术爱好者提供技术内容和技术思想的分享性交流网站。