CF1662H Boundary 题解

可能更好的阅读体验

题目大意

给定一个 \(w\times l\) 的方格，你需要将张方格的周围一圈铺上地砖，然后把中间 \((w-2)\times(l-2)\) 的位置空出。现在已知可以用 \(1\times a\) 的地砖来铺，求 \(a\) 的所有值，升序输出。多组数据，共 \(t\) 组数据。
\(3\le w,l\le 10^9,t\le 100\)

题目解析

首先不难发现有三种铺法：

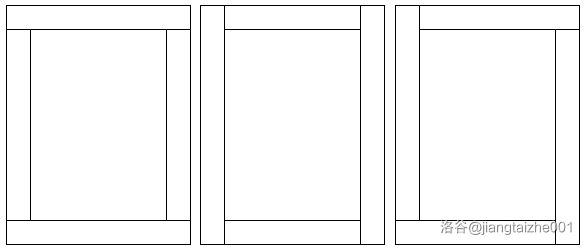
三种铺法对应的长度为 \(w-2,l\) 和 \(w,1,l-2\) 和 \(w-1,l-1\)。
如果一种铺法需要长度为 \(x,y\) 的地砖，显然只需要保证 \(a|x\) 并且 \(a|y\)，直接枚举 \(\gcd(x,y)\) 约数即可。

但是如果你这么写你就会直接 WA on test 2。

我们考虑这么铺：

因为用到了长度为 \(w,w-2\) 的地砖，所以这种铺法只能用 \(1\times2\) 的地砖，此时需要保证 \(w\bmod 2+l\bmod 2=1\)，也就是 \(w,l\) 一奇一偶。

算法复杂度为 \(O\left(\sqrt{w}\log w\right)\)，瓶颈在于枚举排序。

核心代码：

int n,m,ans[maxn],cnt,ret;
int gcd(int x,int y){ return y?gcd(y,x%y):x; }
void add(int x){ int i; for(i=1;i*i<=x;i++) if(x%i==0) ans[++cnt]=i,ans[++cnt]=x/i; return; }
void work(){
	cnt=ret=0; n=read(); m=read(); int i; add(gcd(n-1,m-1)); add(gcd(n-2,m)); add(gcd(n,m-2));
	if(((n&1)&&!(m&1))||((m&1)&&!(n&1))) ans[++cnt]=2;
	sort(ans+1,ans+cnt+1); for(i=1;i<=cnt;i++) if(ans[i]!=ans[i-1]) ret++;
	print(ret),pc(' '); for(i=1;i<=cnt;i++) if(ans[i]!=ans[i-1]) print(ans[i]),pc(' ');
	pc('\n'); return;
}

标签：le,地砖,gcd,int,题解,times,CF1662H,铺法,Boundary
来源： https://www.cnblogs.com/jiangtaizhe001/p/16196154.html