AT5618 [AGC039D] Incenters

Introduction

在这里，你可以同时学习初中数学以及必修一数学。

Solution

首先我们看到内心，他是角平分线的交点，是很不好做的，怎么办呢，三角形有 \(5\) 心，我们考虑将其他几个心与这个内心联系起来，首先外心的坐标是 \((0,0)\) 是显然的，然后重心得坐标同样显然是 \((\frac{x_a+x_b+x_c}{3},\frac{y_a+y_b+y_c}{3})\)，垂心我们有一个欧拉线，他们就可以得到垂心的坐标是\((x_a+x_b+x_c,y_a+y_b+y_c)\)。还有一个旁心是没有用处的，就不管他了。

接下来就是神操作了，我们要将题目中的内心转化成为垂心。

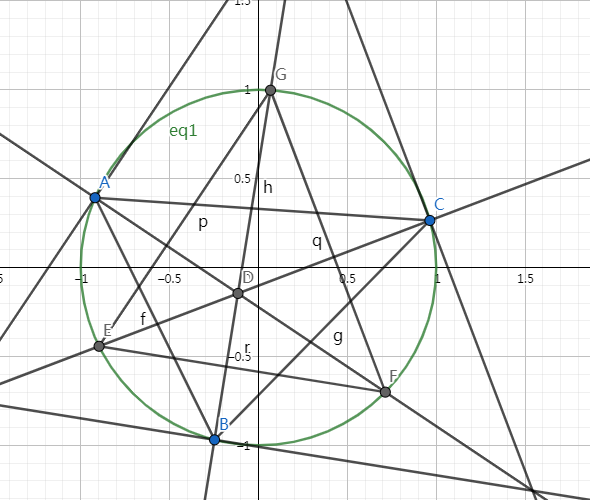
我们假设 \(\triangle ABC\) 的内心为 \(D\)，我们把三条角平分线给引出来，为什么要这么做，因为 \(\frac{\angle A+\angle B+\angle C}{2}=\frac{\pi}{2}\)，然后就得到了一个新的三角形 \(\triangle EFG\) ，我们可以发现的是:

\[\because \angle GEC=\frac{1}{2}\angle B,\angle FEC=\frac{1}{2}\angle A,\angle EGB=\frac{1}{2}\angle C \]

\[\therefore \angle FEG+EGB=\frac{\angle A+\angle B +\angle C }{2}=\frac{\pi}{2} \]

\[\therefore 同理可知 \angle EFG+\angle BGF=\frac{\pi}{2} \]

\[\therefore D是\triangle EFG的垂心 \]

然后我们就把问题从求 \(\triangle ABC\) 的内心转换成了求 \(\triangle EFG\) 的垂心。

然后我们可以发现，因为题目给我们的是点的弧度，所以 \(\triangle EFG\) 每个点的坐标也是可以轻松求出的。

然后就是必修一的内容了。

因为我们现在的做法的复杂度是 \(O(n^3)\) 的，显然无法通过此题。

那么开始优化，我们假设选出的三个点的 \(T_i\) 是 \(x,y,z\) 。

我们可以知道的是现在的表达式是：

\[(\cos(\frac{(x+y)\times \pi}{L})+\cos(\frac{(y+z)\times \pi}{L})-\cos({\frac{(x+z)\times \pi}{L}}),\sin(\frac{(x+y)\times \pi}{L})+\sin(\frac{(y+z)\times \pi}{L})-\sin({\frac{(x+z)\times \pi}{L}})) \]

我们考虑和差化积。那么前面的表达式就是：

\[(-2)\times \sin(\frac{(y-z)\times \pi}{2\times L})\times\sin(\frac{(y+x+z\times 2)\times \pi}{2\times L})=(-2)\times \sin(\frac{(y-z)\times \pi}{2\times L})\times(\sin(\frac{(y+x)\times \pi}{2\times L}))\times \cos(\frac{z\times \pi}{L}+\cos(\frac{(y+x)\times \pi}{2\times L}))\times \sin(\frac{z\times \pi}{L}) \]

然后一下后缀和就好了。

后面一个式子也是同理，然后就优化到了 \(O(n^2)\)

Code

n=read();L=read();
	for (i=1;i<=n;i++)  a[i]=read();
	tot=n*(n-1)*(n-2)/6;
	for (i=n;i>=1;i--) sufs[i]=sufs[i+1]+sin(a[i]/L*PI),sufc[i]=sufc[i+1] +cos(a[i]/L*PI);
	for (A=1;A<=n-2;A++)
	    for (B=A+1;B<=n-1;B++)
	       {
	       	x=x+sin((a[A]+a[B])/L*PI)*(n-B)+2*sin((a[B]-a[A])/2/L*PI)*(cos((a[A]+a[B])/2/L*PI)*sufc[B+1]-sin((a[A]+a[B])/2/L*PI)*sufs[B+1]);
            y=y+cos((a[A]+a[B])/L*PI)*(n-B)+(-2)*sin((a[B]-a[A])/2/L*PI)*(cos((a[A]+a[B])/2/L*PI)*sufs[B+1]+sin((a[A]+a[B])/2/L*PI)*sufc[B+1]);      
		}
	x/=tot;y/=tot;
	printf("%.20lf %.20lf\n",y,x);

标签：cos,frac,times,AT5618,Incenters,angle,pi,AGC039D,sin
来源： https://www.cnblogs.com/oieralbedo/p/15842100.html