【做题记录】树上游戏

• \(\text{P2664}\) 树上游戏

  • 算法：点分治、树上差分

题目：

有一棵树，树的每个节点有个颜色。给一个长度为 \(n\) 的颜色序列，定义 \(s(i,j)\) 为 \(i\) 到 \(j\) 的颜色数量。以及

\[sum_i=\sum_{j=1}^n s(i, j) \]

求所有的 \(sum_i\)。

\(1\leq n,c_i\leq 10^5\)

题解：

这里有两个算法。一个是 \(O(n\log n)\) 的点分治做法，另一个是 \(O(n)\) 的一个 trick，然后会用到一点的树上差分。这里两种都记了吧。

• 法一：点分治 \(O(n\log n)\)

\(\mathcal{P.S.\to}\) 我本题并不是用点分治过的，所以以下内容仅当作我在口胡。

考虑点分治。对于当前分治到的重心，考虑它自己出发至当前分治子树内的所有路径对答案的贡献，和经过它的路径对当前分治子树内点的贡献。

如果是自己子树内的贡献，可以 dfs 暴力求。

那么来考虑子树外至子树内的路径的贡献。

对于每一棵子树，令 \(f_{c_i}\) 表示从重心到其他子树的路径中包含颜色为 \(c_i\)
的条数。所以，我们简单 dfs 一下，对于每个子树 \(x\)，其贡献为 \(\sum\limits_{i\in x} f_{c_i}\)。

感性理解，每一种颜色 \(c_i\) 到当前重心 \(x\) 的贡献就为 \(size_x-f_{c_i}\)。然后这个贡献需要下传，所以标记一下。

总的时间复杂度 \(O(n\log n)\)。

• 法二：奇怪的方法，\(O(n)\)

\(\mathcal{P.S.\to}\) 虽然是用这种方法的，但还是可能不太清楚，代码部分比较模糊，就仅当口胡吧。

首先，考虑每一种颜色对于答案的贡献。

考虑如果将这种颜色的节点删去的影响。

比如在下图中，我们将绿点删去，那么所有绿点相连的边都会被切断：

\[\huge\Downarrow \]

\[\huge\Downarrow \]

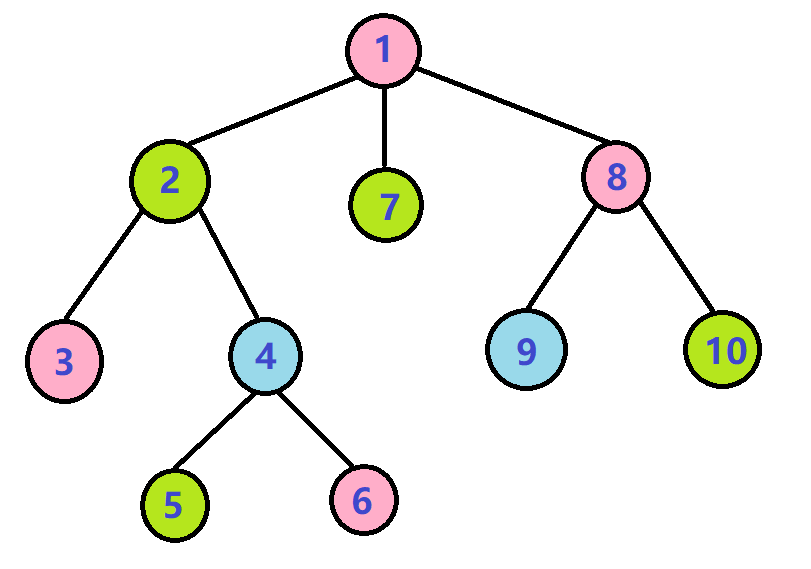
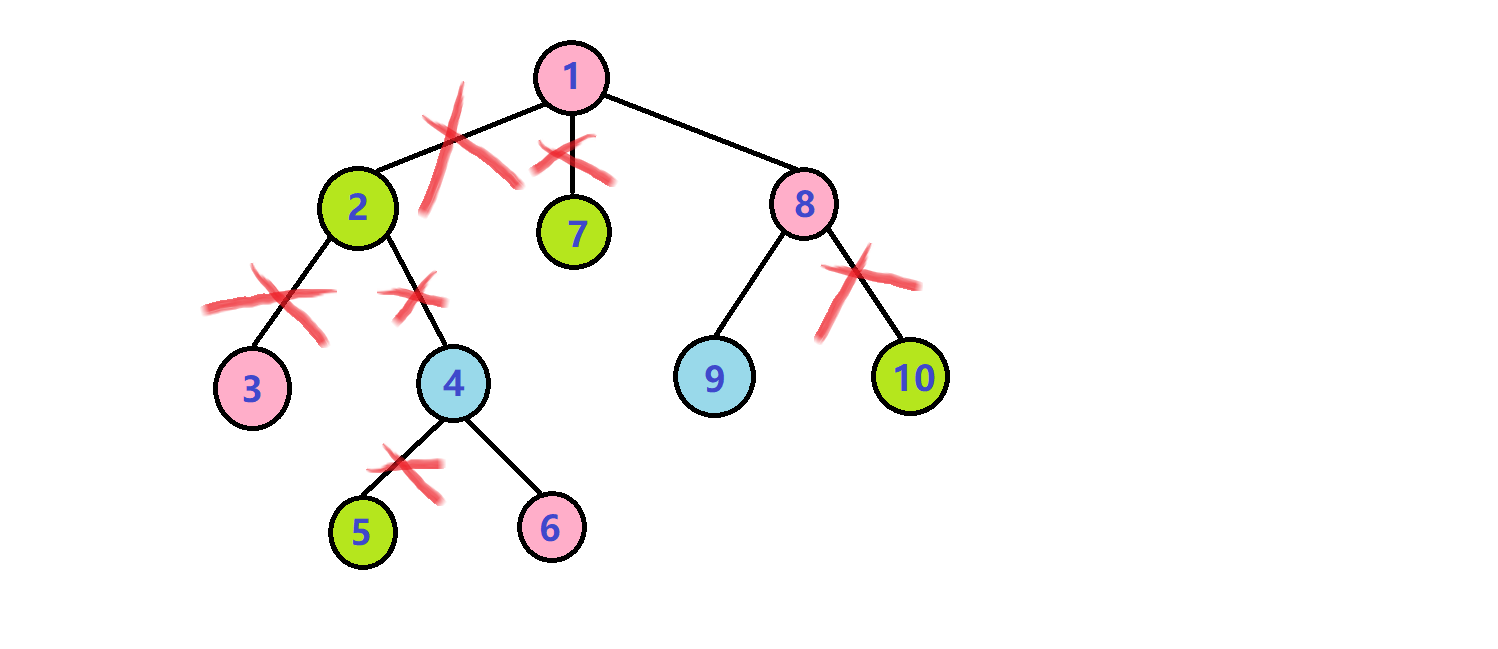
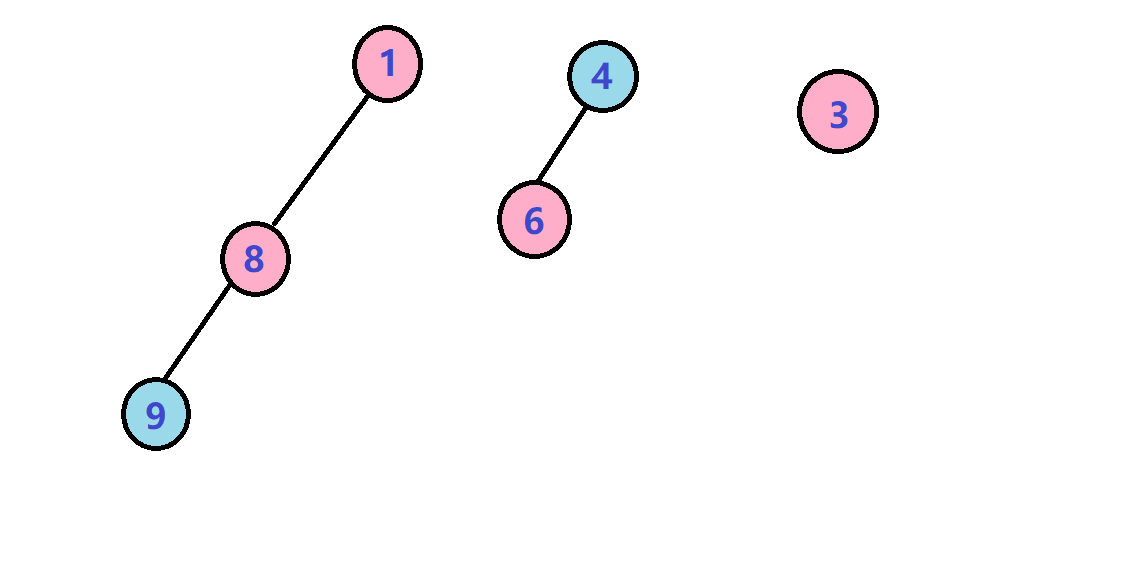
那么，此时剩下的点就会变成一个个小子树（链也是子树）。

我们可以得到两个重要性质:

• 在剩下的子树中，若两点在同一子树，那么删去的颜色对它们的 \(sum\)
  不做贡献；

• 若两点在不同子树，那么该颜色必定做出贡献（因为其为两棵子树联系在一起，必有贡献）

所以，正如上面的图三，我们对于剩下的子树全部加上颜色 \(c\)（这里就是绿色）所带来的贡献。

设 \(f_{i,c}\) 表示对于每种颜色 \(c\)，从 \(i\) 出发不包含这种颜色的路径的条数。

设 \(col\) 为颜色总数，那么可得

\[\therefore sum_i=\sum_{j=1}^{col}(n-f_{i,j}) \]

但是对于每种颜色都要求出删去这种颜色后剩下的子树，时间未免太高。可以考虑差分。将原图中的当前重心的所有子树加上贡献，而再在每一棵子树中存在的以颜色 \(c\) 为重心的子树减去两倍的贡献。

这样就可以 \(O(n)\) 做完了。代码比起上一种好实现得多。

感觉还是讲的不是很透彻，推荐一下这篇 b6e0 的博客，讲得比较好吧。

标签：子树,颜色,游戏,记录,sum,分治,贡献,删去,树上
来源： https://www.cnblogs.com/trsins/p/15777656.html