基环树 dp 学习笔记
作者:互联网
这其实是 N 总发明的算法。
前置芝士:基环树
给定一棵 \(n\) 个点,\(n-1\) 条边的树,任意在树上的两点之间新添加一条边。那么就会形成一个环,整个图也就被称为基环树,如下图所示:
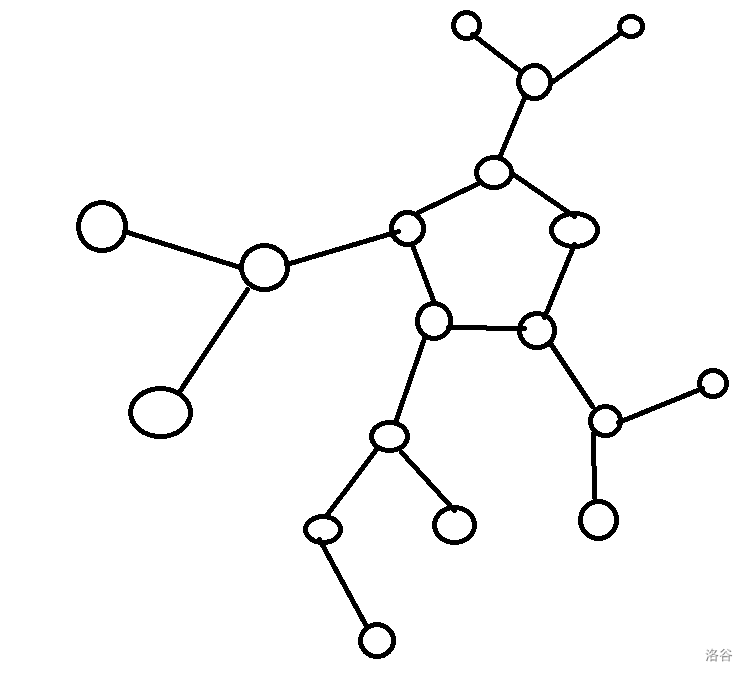
基环树可以简单的理解为所有的树在一个环上。
特别的,如果给基环树中的每一条边指定一个方向,在满足环上的点方向相同时,可以得到以下两种特殊的基环树:
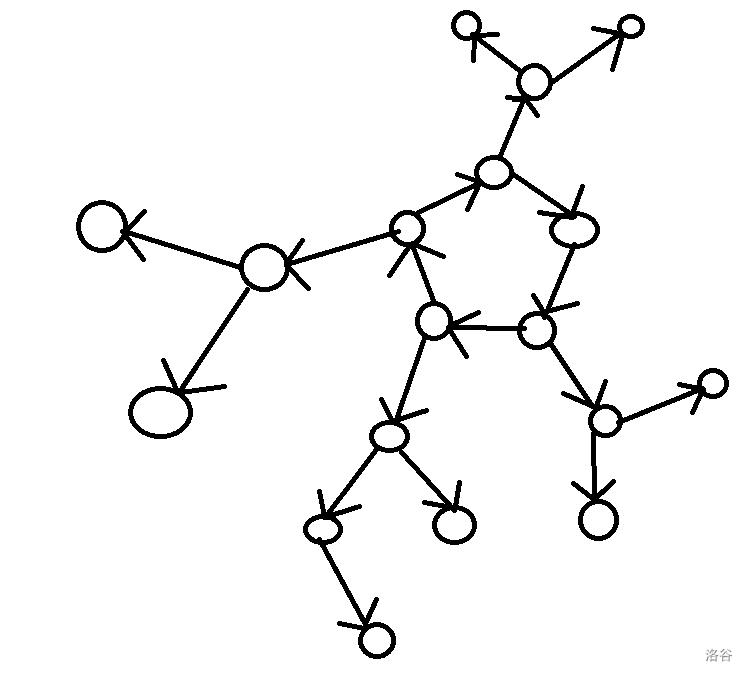
外向树:所有边的方向都从父节点指向子节点,即每个点有且仅有一条入边。
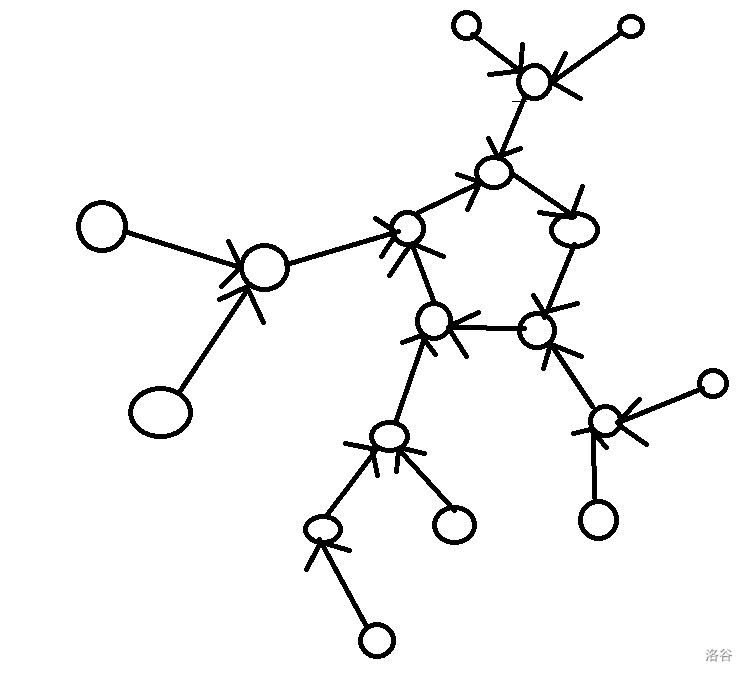
内向树:所有边的方向都从子节点指向父节点,即每个点有且仅有一条出边。
而由若干棵基环树组成的图形就被称为基环树森林。
对于一棵 \(n\) 个顶点的基环树来说,边数也恰好为 \(n\)。
要找到基环树中的环,可以深搜遍历一遍树,同时记录每个点是否被遍历过,是否回溯过和走过该点的前一个点。如果发现当前点已经被遍历过并且当前点还未回溯(有的类似于 Tarjan 算法),那么就说明当前点在环上。接下来不断令当前点为走过当前点的前一个点即可。代码如下:
int n,h[N],idx=1,q[N],preu[N],prew[N];//走到该点前的节点编号,这条边的长度
int cir[N],en[N],cnt;//环上节点的编号,第i个环的结尾是第几个点,环的个数
LL s[N];//以某一点为起点到第 i 的顺时针方向的长度
bool vis[N],ins[N];//是否被访问过,是否没有回溯过
void dfs_cir(int u,int from)//找环,因为要考虑重边,所以只需除去反向边即可
{
vis[u]=ins[u]=true;
for(int i=h[u];~i;i=e[i].nex)
{
if(i==(from^1)) continue;//如果是两个点的环,那么记录不走重复点(v==fa)就会出错
int v=e[i].v;
preu[v]=u,prew[v]=e[i].w;
if(!vis[v]) dfs_cir(v,i);
else if(ins[v])
{
cnt++;
en[cnt]=en[cnt-1];
LL sum=e[i].w;//环的总长度
for(int k=u;k!=v;k=preu[k])
{
s[k]=sum;//前缀和数组
sum+=prew[k];
cir[++en[cnt]]=k;
}
s[v]=sum,cir[++en[cnt]]=v;//别忘了v点,以v为起点到v的顺时针距离就是这个环的长度
}
}
ins[u]=false;
}
例题 [IOI2008] Island
题意
给定 \(n\) 个岛屿,从每个岛屿出发都修建了一座桥。同时每对岛屿都有一艘专用的来往两岛之间的渡船。现在从任意一个岛屿出发,不经过重复的岛屿。当两个岛屿之间存在桥时优先选择通过这座桥。当没有任何间接的桥和以前使用过的渡船的组合可以从其中一个岛屿走到另一个岛屿时,才使用这两个岛屿之间专门的渡船。求经过的桥的总长的最大值(无需经过所有的岛屿)。
思路
对于题中的每一做岛屿,都有一条边,那么最终所有的岛屿和桥就一定构成个 \(n\) 个顶点,\(n\) 条边的基环树森林。
同时注意到题目中要求不走重复岛,且任意的岛屿之间都可以通过渡船到达。那么就可以分别考虑每一棵基环树内部的最长路径,最终将这些最长路径相加即可。
对于每一个基环树内部的最长路径。考虑枚举每两个点之间的距离。这里需要分类讨论:
1.这两个点在同一棵子树上(子树的根在环上)。可以参考树的最长路径的解法。因为不需要知道具体的两个点,只需要知道最长路径。那么就可以以每个节点为根,求出向下走的最长路径和次长路径之和,即通过该点的在同一棵树内的最长路径。
2.而对于不在同一棵子树上的点,这两点之间的路径显然就要经过环。同样根据上一种情况的思想,不枚举这两个节点,而是枚举环上的点,那么就可以将总路径分为三个部分,如下图所示:
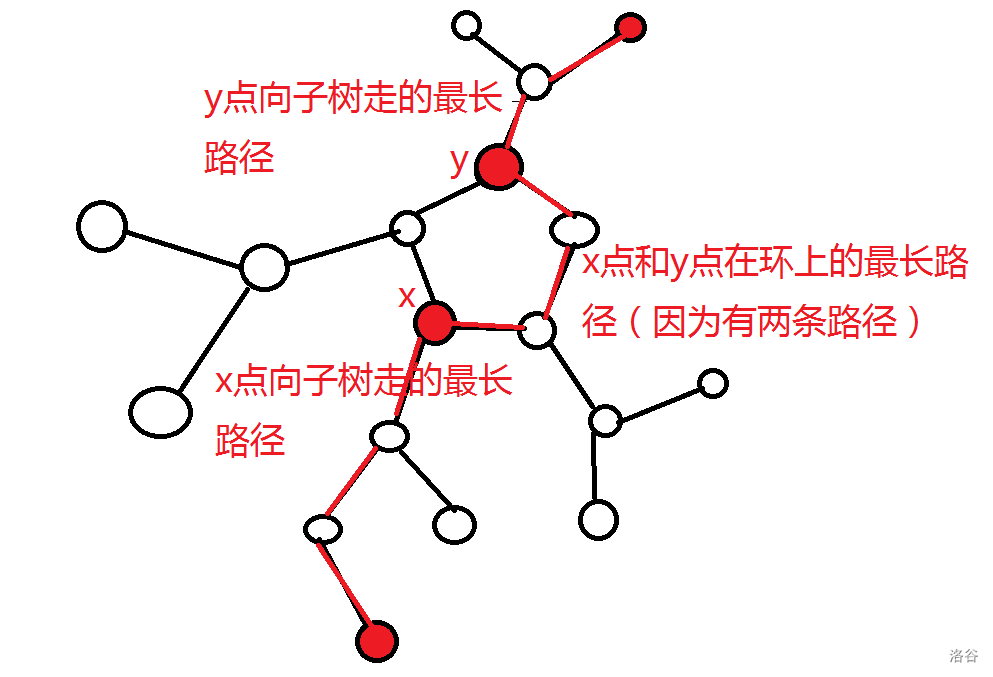
向子树走的两个部分都可以在求第一种情况时预处理得到,如果直接枚举基环树上的两个点之间的路径,加上求路径的 \(O(n)\) 时间,那么总的时间复杂度就为 \(O(n^3)\)。显然无法接受,考虑对枚举过程进行优化。
可以发现,如果基环树上的两个点位置互换,答案不变。于是就可以规定 \(x\) 点在 \(y\) 的顺时针(逆时针也可以)方向。记基环树上两个点之间的最大距离为 \(S(x,y)\), \(x\) 点向子数中走的最长距离为 \(d[x]\),那么就可以得到:
\(ans=\max(d[x]+d[y]+S(x,y))\)。
如果令基环树上的某一点为起点,记 \(s[x]\) 为点 \(x\) 到起点的顺时针方向距离。那么就可以得到:
\(ans=\max(d[x]+s[x]+d[x]-s[y])\)。
其中的 \(d[x]+s[x]\) 为常量,也就可以将题目转化为求 \(\max(d[y]-s[y])\)。注意到这样做有一个问题,\(d[x]-d[y]\) 不一定就是 \(S(x,y)\),也可能是 \(sum-d[x]+d[y]\)。对于这个问题,可以使用破环成链的技巧。将环变成一条链并延长一倍。同时在延长的链上,\(s[x]\) 也要加上环的长度 \(sum\),这样就可以枚举 \(d[x]-d[y]\) 和 \(sum-d[x]+d[y]\) 两种情况了。
还有一些细节见代码。
code:
#include<cstdio>
#include<cstring>
using namespace std;
#define LL long long //数据范围会爆int
const int N=1e6+10;
const int M=2e6+10;
struct edge{
int v,w,nex;
}e[M];
int n,h[N],idx=1,q[N],preu[N],prew[N];//走到该点前的节点编号,这条边的长度
LL s[N],sum[N*2],d[N*2],ans;//前缀和,为了方便破环成链,单独储存并且需要开两倍,ans是当前基环树的最长距离,因为有两种情况,所以设为全局变量
int cir[N],en[N],cnt;//环上节点的编号,第i个环的结尾是第几个点,环的个数
bool vis[N],ins[N];//是否被访问过,是否没有回溯过
LL max(LL a,LL b){return a>b?a:b;}
LL min(LL a,LL b){return a<b?a:b;}
void add(int u,int v,int w)
{
e[++idx].v=v;
e[idx].nex=h[u];
e[idx].w=w;
h[u]=idx;
}
void dfs_cir(int u,int from)//找环,因为要考虑重边,所以只需除去反向边即可
{
vis[u]=ins[u]=true;
for(int i=h[u];~i;i=e[i].nex)
{
if(i==(from^1)) continue;
int v=e[i].v;
preu[v]=u,prew[v]=e[i].w;
if(!vis[v]) dfs_cir(v,i);
else if(ins[v])
{
cnt++;
en[cnt]=en[cnt-1];
LL sum=e[i].w;//环的总长度
for(int k=u;k!=v;k=preu[k])
{
s[k]=sum;//前缀和数组
sum+=prew[k];
cir[++en[cnt]]=k;
}
s[v]=sum,cir[++en[cnt]]=v;//别忘了v点
}
}
ins[u]=false;
}
LL dfs_d(int u) //向下走的最长距离以及第一种情况
{
vis[u]=true;
LL d1=0,d2=0;//最长和次长
for(int i=h[u];~i;i=e[i].nex)
{
int v=e[i].v;
if(vis[v]==true) continue;
LL dist=dfs_d(v)+e[i].w;//即d[u]的一个可能取值
if(d1<=dist) d2=d1,d1=dist;
else if(d2<dist) d2=dist;
}
ans=max(ans,d1+d2); //情况一
return d1;
}
int main()
{
scanf("%d",&n);
memset(h,-1,sizeof(h));
for(int v,w,u=1;u<=n;u++)
{
scanf("%d%d",&v,&w);
add(u,v,w),add(v,u,w);
}
for(int i=1;i<=n;i++)
if(!vis[i]) dfs_cir(i,-1);//找到一棵基环树
LL res=0;//最终答案
memset(vis,0,sizeof(vis));//上面的vis用于找环,下面的vis用于求最长路径
for(int i=1;i<=en[cnt];i++) vis[cir[i]]=true;//树上的最长路径不经过环
for(int i=1;i<=cnt;i++) //情况2
{
ans=0;
int siz=0;//环的大小
for(int j=en[i-1]+1;j<=en[i];j++)//枚举这个环上的点
{
int k=cir[j];//从环上的最后一点开始枚举
d[++siz]=dfs_d(k);//每个点为根的子树向下走的最长距离
sum[siz]=s[k];
}
for(int j=1;j<=siz;j++) d[j+siz]=d[j],sum[j+siz]=sum[j]+sum[siz];//最后一个点就是起点,起点到这个点的顺时针距离也就是这个环的长度
int hh=0,tt=-1;
for(int j=1;j<=siz*2;j++)
{
if(hh<=tt&&j-q[hh]>=siz) hh++;//超出了环
if(hh<=tt) ans=max(ans,d[j]+d[q[hh]]+sum[j]-sum[q[hh]]);//注意是sum不是s
while(hh<=tt&&d[q[tt]]-sum[q[tt]]<=d[j]-sum[j]) tt--;
q[++tt]=j;
}
res+=ans;
}
printf("%lld\n",res);
return 0;
}
例题 [ZJOI2008]骑士
题意
给定 \(n\) 个骑士,每个骑士都有一个战斗力,以及他讨厌的骑士。求选出若干个骑士,在没有任何骑士被讨厌的情况下战斗力之和的最大值。
思路
很明显,如果把讨厌关系当成一条边,那么所有骑士都有一条出边,他们的关系显然构成一棵内向基环树或内向基环树森林。
可以联想本题的简化版没有上司的舞会。对于森林中的每一棵基环树,都可以将环上的一条边断开,记这条边的两点为 \(P,Q\)。断开后得到的图就是一个以 \(P\) 为根的树(也可以以 \(Q\) 为根)接下来对于所有选择的方案就可以分为两类:
1.不选 \(P\),那么 \(P->Q\) 的这条边就显然没有意义了,直接模仿舞会进行树形 dp 即可。
2.选择 \(Q\),那么 \(Q\) 就必然无法选择。在树形 dp 的过程中特判一下 \(Q\) 点就可以了。
需要注意的是,这样分类就已经包含了所有合法的选择方案,也就没必要再去枚举环上其他的边了。所以最终的时间复杂度就为 \(O(N)\),不过常数有一点大。需要用到一点卡常技巧。
code:
#include<cstdio>
using namespace std;
#define LL long long
const int N=1e6+10;
const int M=1e6+10;
const LL INF=1e18;//10^6*10^6会爆int
int n,h[N],idx,val[N];
bool broken[N];//是否断开
struct edge{
int v,nex;
}e[M];
bool vis[N],ins[N];
LL ans,f1[N][2],f2[N][2];//方案1,方案2
LL max(LL a,LL b){return a>b?a:b;}
inline void add(int u,int v)
{
e[++idx].v=v;
e[idx].nex=h[u];
h[u]=idx;
}
void dfs_dp(int u,int q,LL f[][2])//当前节点,特判不选的节点,是哪一种方案
{
for(int i=h[u];i;i=e[i].nex)
{
if(broken[i]) continue;
int v=e[i].v;
dfs_dp(v,q,f);
f[u][0]+=max(f[v][0],f[v][1]);
}
if(u==q) f[u][1]=-INF;
else
{
f[u][1]=val[u];
for(int i=h[u];i;i=e[i].nex)
{
if(broken[i]) continue;
int v=e[i].v;
f[u][1]+=f[v][0];
}
}
}
void dfs_cir(int u,int from)
{
vis[u]=ins[u]=true;
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
// if(i==(from^1)) continue; 这里因为是有向图,就不需要特判反边了
if(!vis[v]) dfs_cir(v,i);
else if(ins[v]) //其实是为了防止在一棵基环树内重复枚举断边
{
broken[i]=true;
dfs_dp(v,-1,f1);
dfs_dp(v,u,f2);
ans+=max(f1[v][0],f2[v][1]);
}
}
ins[u]=false;
}
int main()
{
scanf("%d",&n);
for(int v,u=1;u<=n;u++)
{
scanf("%d%d",&val[u],&v);
add(v,u); //内向基环树,节点从父亲指向儿子便于树形dp
}
for(int i=1;i<=n;i++)
if(!vis[i]) dfs_cir(i,-1);
printf("%lld\n",ans);
return 0;
}
例题 创世纪
题意
给定 \(n\) 种元素,第 \(i\) 种元素能够限制第 \(A[i]\) 种元素。现在要投放若干种元素,在满足每种投放的元素都有至少一种没有被投放的元素限制它的前提下,求最多投放的元素种类。
思路
把限制关系看成一条边,那么每种元素都有一条出边,和上题类似,也就构成了一棵内向基环树或内向基环树森林。
状态的设计也和上一题类似,\(f[u][0]\) 的转移方程也一样,有不同点的地方就是关于 \(f[u][1]\) 的转移方程。
对于每一个父亲,由内向基环树的性质可以知道,它的每一个儿子都可以限制它,根据题意,必然有一个儿子不选。而不选这个儿子,其他儿子的选法也就没有限制了,现在要使其他儿子选法得到的值最大,而所有儿子最大的取值之和就是 \(f[u][0]\),再减去当前节点的贡献 \(\max(f[v][1],f[v][0])\)。就是其他儿子的最优解了。同时当前节点的状态只能是不选,也就是 \(f[v][1]\),于是就可以得到状态转移方程:
\(f[u][1]=\max(f[u][0]-\max(f[v][1],f[v][0])+f[v][0])+1\)。
接下来考虑断边,设断边的两个端点为 \(P,Q\),且边由 \(P\) 指向 \(Q\),与上题要求没有讨厌骑士不同,本题需要考虑的是限制条件,也就是断边:
1.选择 \(P->Q\) 这个限制条件,那么就是用 \(P\) 来限制 \(Q\),显然 \(Q\) 就必选, \(P\) 就必不选。
2.不选 \(P->Q\) 这个限制条件,那么直接断开即可,没有任何影响,这种情况的答案就是 \(\max(f[P][0],f[P][1])\)。
code:
#include<cstdio>
using namespace std;
const int N=1e6+10;
const int INF=0x3f3f3f3f;
int f1[N][2],f2[N][2],n,h[N],idx,ans;
struct edge{
int v,nex;
}e[N];
bool vis[N],ins[N],broken[N];
void add(int u,int v)
{
e[++idx].v=v;
e[idx].nex=h[u];
h[u]=idx;
}
int max(int a,int b){return a>b?a:b;}
void dfs_dp(int u,int q,int f[][2])
{
for(int i=h[u];i;i=e[i].nex)
{
if(broken[i]) continue;
int v=e[i].v;
dfs_dp(v,q,f);
f[u][0]+=max(f[v][1],f[v][0]);
}
if(u==q)//q点已经被p点限制,对于儿子就没有特殊要求了
{
f[u][1]=f[u][0]+1;//q点是必选的
f[u][0]=-INF;
return ;
}
f[u][1]=-INF;
for(int i=h[u];i;i=e[i].nex)
{
if(broken[i]) continue;
int v=e[i].v;
f[u][1]=max(f[u][1],f[u][0]-max(f[v][0],f[v][1])+f[v][0]+1);
}
}
void dfs_cir(int u)
{
vis[u]=ins[u]=true;
for(int i=h[u];i;i=e[i].nex)
{
int v=e[i].v;
if(!vis[v]) dfs_cir(v);
else if(ins[v])
{
broken[i]=true;
dfs_dp(v,-1,f1);
dfs_dp(v,u,f2);
ans+=max(max(f1[v][1],f1[v][0]),f2[v][0]);
}
}
ins[u]=false;
}
int main()
{
scanf("%d",&n);
for(int v,u=1;u<=n;u++)
{
scanf("%d",&v);
add(v,u);//内向基环树,反向建边便于树形dp
}
for(int i=1;i<=n;i++)
if(!vis[i]) dfs_cir(i);
printf("%d\n",ans);
return 0;
}
标签:int,max,LL,笔记,ins,基环树,dfs,dp 来源: https://www.cnblogs.com/NLCAKIOI/p/14975178.html