有关KKT条件

2021-06-27 09:35:31 作者：互联网

来源：https://zhuanlan.zhihu.com/p/26514613

0.什么是KKT条件

本文从本科高数（微积分）中的有条件极值的Lagrange乘数法入手，一步步推导到KKT条件. 但在讲述推导过程之前，我想先给出KKT条件：

对于具有等式和不等式约束的一般优化问题

$\begin{array}{l} \min {\rm{ }}f({\bf{x}})\\ s.t.{\rm{ }}{g_j}({\bf{x}}) \le 0(j = 1,2, \cdots ,m)\\ {\rm{ }}{h_k}({\bf{x}}) = 0(k = 1,2, \cdots ,l) \end{array}$

KKT条件给出了判断 ${{\bf{x}}^*}$ 是否为最优解的必要条件，即：

$\left\{ \begin{array}{l} \frac{{\partial f}}{{\partial {x_i}}} + \sum\limits_{j = 1}^m {{\mu _j}} \frac{{\partial {g_j}}}{{\partial {x_i}}} + \sum\limits_{k = 1}^l {{\lambda _k}\frac{{\partial {h_k}}}{{\partial {x_i}}}} = 0,{\rm{ }}\left( {i = 1,2,...,n} \right)\\ {h_k}\left( {\bf{x}} \right) = 0,{\rm{ (}}k = 1,2, \cdots ,l)\\ {\mu _j}{g_j}\left( {\bf{x}} \right) = 0,{\rm{ (}}j = 1,2, \cdots ,m)\\ {\mu _j} \ge 0. \end{array} \right.$

1. 等式约束优化问题（Lagrange乘数法）

对于这部分内容，其实本科高数课程中已学过，因此本文直接给出结论，并补充一些我的理解与总结，它能帮助理解不等式约束中的一些内容，具体的推导过程在同济7版的高数下册（P.116-118）中已写的较详细。

所谓的等式约束优化问题是指

$minf(x_{1} ,x_{2} ,...,x_{n} )$
$s.t.h_{k} (x_{1} ,x_{2} ,...,x_{n} )=0$

我们令 $L({\bf{x}},{\bf{\lambda }}) = f({\bf{x}}) + \sum\limits_{k = 1}^l {{\lambda _k}{h_k}({\bf{x}})}$ ，函数 $L(x,y)$ 称为Lagrange函数，参数 $\lambda$ 称为Lagrange乘子.

再联立方程组： $\left\{ \begin{array}{l} \frac{{\partial L}}{{\partial {x_i}}} = 0{\rm{ ( }}i{\rm{ = 1 ,2 ,}} \cdots {\rm{,}}n{\rm{ ) }}\\ \frac{{\partial L}}{{\partial {\lambda _k}}} = 0{\rm{ ( }}k{\rm{ = 1 ,2 ,}} \cdots {\rm{,}}l{\rm{ ) }} \end{array} \right.$ ，

得到的解为可能极值点，由于我们用的是必要条件，具体是否为极值点需根据问题本身的具体情况检验. 这个方程组称为等式约束的极值必要条件.

上式我们对 $n$ 个 $x_{i}$ 和 $l$ 个 $\lambda _{k}$ 分别求偏导，回想一下在无约束优化问题 $f(x_{1}, x_{2},...,x_{n} )=0$ 中，我们根据极值的必要条件，分别令 $\frac{\partial f}{\partial x_{i} } =0$ ，求出可能的极值点. 因此可以联想到：等式约束下的Lagrange乘数法引入了 $l$ 个Lagrange乘子，或许我们可以把 $\lambda _{k}$ 也看作优化变量（ $x_{i}$ 就叫做优化变量）. 相当于将优化变量个数增加到 $(n+l)$ 个， $x_{i}$ 与 $\lambda _{k}$ 一视同仁，均为优化变量，均对它们求偏导.

2. 不等式约束优化问题

以上我们讨论了等式约束的情形，接下来我们来介绍不等式约束的优化问题.我们先给出其主要思想：转化的思想——将不等式约束条件变成等式约束条件.具体做法：引入松弛变量.松弛变量也是优化变量，也需要一视同仁求偏导.

具体而言，我们先看一个一元函数的例子：

$minf(x)$
$s.t. g_{1}(x) =a-x\leq 0 \\g_{2}(x) =x-b\leq 0$

（注：优化问题中，我们必须求得一个确定的值，因此不妨令所有的不等式均取到等号，即 $\leq$ 的情况.）

对于约束 $g_{1}$ 和 $g_{2}$ ，我们分别引入两个松弛变量 $a_{1}^{2}$ 和 $b_{1}^{2}$ ，得到 $h_{1} (x,a_{1} )=g_{1} +a_{1}^{2} =0$ 和 $h_{2} (x,b_{1} )=g_{2} +b_{1}^{2} =0$ .注意，这里直接加上平方项 $a_{1}^{2}$ 、 $b_{1}^{2}$ 而非 $a_{1}$ 、 $b_{1}$ ，是因为 $g_{1}$ 和 $g_{2}$ 这两个不等式的左边必须加上一个正数才能使不等式变为等式.若只加上 $a_{1}$ 和 $b_{1}$ ，又会引入新的约束 $a_{1} \geq 0$ 和 $b_{1} \geq 0$ ，这不符合我们的意愿.

由此我们将不等式约束转化为了等式约束，并得到Lagrange函数

$L(x,a_{1} ,b_{1} ,\mu _{1} ,\mu _{2} )=f(x)+\mu _{1}(a-x+a_{1}^{2} )+\mu _{2}(x-b+b_{1}^{2} )$

我们再按照等式约束优化问题（极值必要条件）对其求解，联立方程

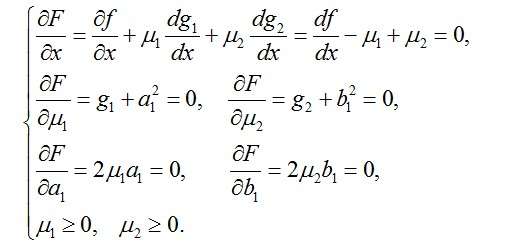
（注：这里的 $\mu _{1} \geq 0$ ， $\mu _{2} \geq 0$ 先承认，我们待会再解释！（先上车再买票，手动斜眼）实际上对于不等式约束前的乘子，我们要求其大于等于0）

得出方程组后，便开始动手解它. 看到第3行的两式 $\mu _{1} a_{1} =0$ 和 $\mu _{1} a_{1} =0$ 比较简单，我们就从它们入手吧~

对于 $\mu _{1} a_{1} =0$ ，我们有两种情况：

情形1： $\mu _{1} =0,a_{1} \ne 0$

此时由于乘子 $\mu _{1} =0$ ，因此 $g_{1}$ 与其相乘为零，可以理解为约束 $g_{1}$ 不起作用，且有 $g_{1}(x) =a-x< 0$ .

情形2： $\mu _{1} \geq 0,a_{1} =0$

此时 $g_{1}(x) =a-x= 0$ 且 $\mu _{1} > 0$ ，可以理解为约束 $g_{1}$ 起作用，且有 $g_{1}(x)=0$ .

合并情形1和情形2得： $\mu _{1}g_{1}=0$ ，且在约束起作用时 $\mu _{1} > 0$ ， $g_{1}(x)=0$ ；约束不起作用时 $\mu _{1}=0$ ， $g_{1}(x)<0$ .

同样地，分析 $\mu _{2}b_{1}=0$ ，可得出约束 $g_{2}$ 起作用和不起作用的情形，并分析得到 $\mu _{2}g_{2}=0$ .

由此，方程组（极值必要条件）转化为

$\left\{ \begin{array}{l} \frac{{df}}{{dx}} + {\mu _1}\frac{{d{g_1}}}{{dx}} + {\mu _2}\frac{{d{g_2}}}{{dx}} = 0,\\ {\mu _1}{g_1}\left( x \right) = 0,{\mu _2}{g_2}\left( x \right) = 0,\\ {\mu _1} \ge 0,{\mu _2} \ge 0. \end{array} \right.$

这是一元一次的情形.类似地，对于多元多次不等式约束问题

$\begin{array}{l} \min {\rm{ }}f({\bf{x}})\\ s.t.{\rm{ }}{g_j}({\bf{x}}) \le 0{\rm{ }}(j = 1,2, \cdots ,m) \end{array}$

我们有

$\left\{ \begin{array}{l} \frac{{\partial f\left( {{x^*}} \right)}}{{\partial {x_i}}} + \sum\limits_{j = 1}^m {{\mu _j}\frac{{\partial {g_j}\left( {{x^*}} \right)}}{{\partial {x_i}}}} = 0{\rm{ }}\left( {i = 1,2,...,n} \right),\\ {\mu _j}{g_j}\left( {{x^*}} \right) = 0{\rm{ }}\left( {j = 1,2,...,m} \right),\\ {\mu _j} \ge 0{\rm{ }}\left( {j = 1,2,...,m} \right). \end{array} \right.$

上式便称为不等式约束优化问题的KKT（Karush-Kuhn-Tucker）

标签：不等式,KKT,有关,Lagrange,约束,等式,条件,优化
来源： https://www.cnblogs.com/nlpers/p/14939888.html