第一个突破O(n^2)的排序算法；是简单插入排序的改进版；它与插入排序的不同之处在于，它会优先比较距离较远的元素。

希尔排序(Shell Sort)，也称递减增量排序算法，1959年Shell发明。是插入排序的一种高速而稳定的改进版本。

希尔排序是先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行依次直接插入排序。

一、基本思想

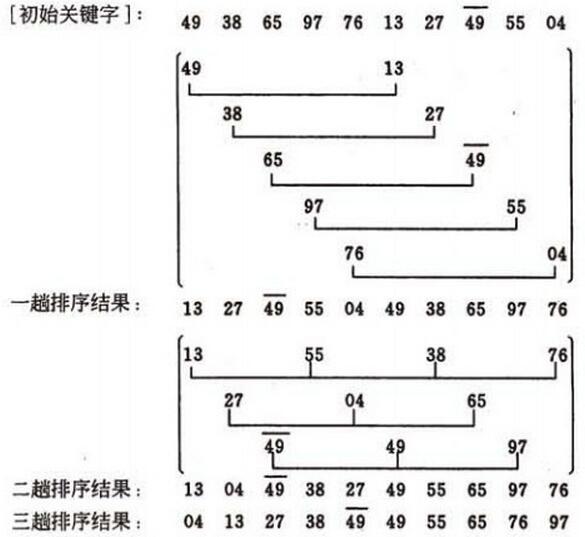
将待排序数组按照步长gap进行分组，然后将每组的元素利用直接插入排序的方法进行排序；每次再将gap折半减小，循环上述操作；当gap=1时，利用直接插入，完成排序。

可以看到步长的选择是希尔排序的重要部分。只要最终步长为1任何步长序列都可以工作。一般来说最简单的步长取值是初次取数组长度的一半为增量，之后每次再减半，直到增量为1。更好的步长序列取值可以参考维基百科。

二、算法描述

1. 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；（一般初次取数组半长，之后每次再减半，直到增量为1）
2. 按增量序列个数k，对序列进行k趟排序；
3. 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m的子序列，分别对各子表进行直接插入排序。仅增量因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度。

2.1 希尔排序图解

希尔排序应运而生了，希尔排序通过加大插入排序中元素的间隔，并在这些有间隔的元素中进行插入排序，从而使数据项能够大跨度的移动。当这些数据项排过一趟序后，希尔排序算法减小数据项的间隔再进行排序，依次进行下去，最后间隔为1时，就是我们上面说的简单的直接插入排序。

下图显示了增量为4时对包含10个数组元素进行排序的第一个步骤，首先对下标为0,4,8的元素进行排序，完成排序之后，算法右移一步，对1,5,9号元素进行排序，依次类推，直到所有的元素完成一趟排序，也就是说间隔为4的元素都已经排列有序。

当我们完成4-增量排序之后，在进行普通的插入排序，即1-增量排序，会比前面直接执行简单插入排序要快很多。

2.2 排序间隔选取

对于10个元素，我们选取4的间隔，那么100个数据，1000个数据，甚至更多的数据，我们应该怎么选取间隔呢？

希尔的原稿中，他建议间隔选为N/2，也就是每一趟都将排序分为两半，因此对于N=100的数组，逐渐减小的间隔序列为：50,25,12，6,3,1。这个方法的好处是不需要在开始排序前为找到初始序列的间隔而计算序列，只需要用2整除N。但是这已经被证明并不是最好的序列。

间隔序列中的数字互质是很重要的指标，也就是说，除了1，他们没有公约数。这个约束条件使得每一趟排序更有可能保持前一趟排序已经排好的结果，而希尔最初以N/2的间隔的低效性就是没有遵守这个准则。

所以一种希尔的变形方法是用2.2来整除每一个间隔，对于n=100的数组，会产生序列45，20，9,4,1。这比用2会整除会显著的改善排序效果。

还有一种很常用的间隔序列：knuth间隔序列3h+1

但是无论是什么间隔序列，最后必须满足一个条件，就是逐渐减小的间隔最后一定要等于1，因此最后一趟排序一定是简单的插入排序。

三、代码实现

以下是我自己的实现，可以看到实现很幼稚，但是好处是理解起来很简单。因为没有经过任何的优化，所以不建议大家直接使用。建议对比下方的维基百科官方实现代码，特别是步长取值策略部分。

/**
 * 希尔排序
 * <p>
 * 1. 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；（一般初次取数组半长，之后每次再减半，直到增量为1）
 * 2. 按增量序列个数k，对序列进行k趟排序；
 * 3. 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m的子序列，分别对各子表进行直接插入排序。
 * 仅增量因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度。
 *
 * @param arr 待排序数组
 */
public static void shellSort(int[] arr) {
    int gap = arr.length / 2;
    for (; gap > 0; gap /= 2) {      //不断缩小gap，直到1为止
        for (int j = 0; (j + gap) < arr.length; j++) {     //使用当前gap进行组内插入排序
            for (int k = 0; (k + gap) < arr.length; k += gap) {
                if (arr[k] > arr[k + gap]) {
                    int temp = arr[k + gap];      //交换操作
                    arr[k + gap] = arr[k];
                    arr[k] = temp;
                    System.out.println("Sorting:  " + Arrays.toString(arr));
                }
            }
        }
    }
}

注意：

1. 第一层for循环表示一共有多少个增量。增量的序列的个数，就是希尔排序的趟数。上面的增量序列为：arr.length/2, arr.length/2/2, arr.length/2/2/2, .... 2, 1
2. 里层的两个for循环，实际上就是以一个gap拆分为一组的组内插入排序。

下面是维基百科官方实现，大家注意gap步长取值部分：

/**
 * 希尔排序（Wiki官方版）
 * <p>
 * 1. 选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；（注意此算法的gap取值）
 * 2. 按增量序列个数k，对序列进行k趟排序；
 * 3. 每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m的子序列，分别对各子表进行直接插入排序。
 * 仅增量因子为1时，整个序列作为一个表来处理，表长度即为整个序列的长度。
 *
 * @param arr 待排序数组
 */
public static void shellSort(int[] arr) {
    int gap = 1, i, j, len = arr.length;
    int temp;
    while (gap < len / 3)
        gap = gap * 3 + 1;      // <O(n^(3/2)) by Knuth,1973>: 1, 4, 13, 40, 121, ...
    for (; gap > 0; gap /= 3) {
        for (i = gap; i < len; i++) {
            temp = arr[i];
            for (j = i - gap; j >= 0 && arr[j] > temp; j -= gap)
                arr[j + gap] = arr[j];
            arr[j + gap] = temp;
        }
    }
}

下面我们通过knuth间隔序列来实现希尔排序：

3.1 knuth间隔序列的希尔排序算法实现

//希尔排序 knuth 间隔序列 3h+1
public static void shellKnuthSort(int[] array) {
    System.out.println("原数组为" + Arrays.toString(array));
    int step = 1;
    int len = array.length;
    while (step <= len / 3) {
        step = step * 3 + 1;//1,4,13,40......
    }
    while (step > 0) {
        //分别对每个增量间隔进行排序
        for (int i = step; i < len; i++) {
            int temp = array[i];
            int j = i;
            while (j > step - 1 && temp <= array[j - step]) {
                array[j] = array[j - step];
                j -= step;
            }
            array[j] = temp;
        }//end for
        System.out.println("间隔为" + step + "的排序结果为" + Arrays.toString(array));
        step = (step - 1) / 3;
    }//end while(step>0)

    System.out.println("最终排序：" + Arrays.toString(array));
}

测试结果：

public static void main(String[] args) {
    int[] array = {4,2,8,9,5,7,6,1,3,10};
    shellKnuthSort(array);
}

3.2 间隔为2h的希尔排序

//希尔排序 间隔序列2h
public static void shellSort(int[] array) {
    System.out.println("原数组为" + Arrays.toString(array));
    int step;
    int len = array.length;
    for (step = len / 2; step > 0; step /= 2) {
        //分别对每个增量间隔进行排序
        for (int i = step; i < array.length; i++) {
            int j = i;
            int temp = array[j];
            if (array[j] < array[j - step]) {
                while (j - step >= 0 && temp < array[j - step]) {
                    array[j] = array[j - step];
                    j -= step;
                }
                array[j] = temp;
            }
        }
        System.out.println("间隔为" + step + "的排序结果为" + Arrays.toString(array));
    }
}

测试结果：

四、性能分析

以下是希尔排序复杂度:

平均时间复杂度	最好情况	最坏情况	空间复杂度
O(nlog2 n)	O(nlog2 n)	O(nlog2 n)	O(1)

标签：arr,int,算法,gap,希尔,序列,array,排序
来源： https://www.cnblogs.com/ciel717/p/16366533.html