JavaScript 数学曲线—阿基米德螺线

引子

最近在研究曲线运动的时候，尝试了用 AI 导出的 SVG 路径之后，发现有些还是回归到数学中更合适一些。搜集了一些资料，尝试后总结一下。

• Origin
• My GitHub

简介

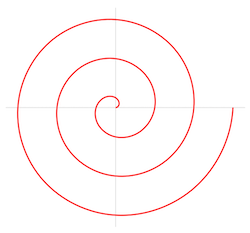
阿基米德螺旋是以公元前 3 世纪希腊数学家阿基米德命名的螺旋。它是一个轨迹，对应于一个点在一段时间内的位置，该点沿着一条以恒定角速度旋转的线以恒定速度离开一个固定点。在极坐标系中的公式描述：

当 c = 1 时，就是通常所说的阿基米德螺旋。

公式说明：

• r ：径向距离。
• a ：常数，起始点与极坐标中心的距离。
• b ：常数，控制螺旋相邻两条曲线之间的距离。
• θ ：极角。

实际应用有：

• 阿基米德螺线可以在螺旋天线中找到，它可以在很宽的频率范围内工作。
• 要求患者画一个阿基米德螺旋线是一种量化人类颤抖的方法，这些信息有助于诊断神经系统疾病。
• 阿基米德螺旋线也用于数字光处理（DLP）投影系统，以最小化“彩虹效应”，使其看起来好像同时显示多种颜色，而实际上是由于红色、绿色和蓝色的循环速度非常快。
• 阿基米德螺旋线在食品微生物学中用于通过螺旋盘量化细菌浓度。

绘制

用 canvas 绘制曲线，canvas 的坐标系是笛卡尔坐标系，需要做一个转换。

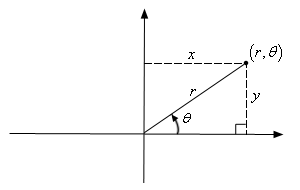
由上面的图可知取一个点有下面的数学转换关系：

x = rcos(θ)
y = rsin(θ)
θ = arctan(y/x)

结合极坐标系的公式可得：

x = (a + bθ)cos(θ)
y = (a + bθ)sin(θ)

这是示例，绘制主要逻辑代码：

function draw() {
  let a = 0, b = 10, angle = 0;
  let x = 0, y = 0, points = [];
  const acceleration = 0.1, circleNum = 2;
  // 注意这里角度的递增，以 2 * Math.PI 为基准进行比较，控制画多少圈
  while (angle <= circleNum * 2 * Math.PI) {
    x = (a + b * angle) * Math.cos(angle);
    y = (a + b * angle) * Math.sin(angle);
    points.push([x, y]);
    angle = angle + acceleration;
  }
  // 实现把点绘制成线的方法
  line({ points: points});
}

改变其中的参数，会产生很多不同的图形，有的看起来并不是曲线。

参考资料

• Archimedean spiral Wiki
• Archimedean spiral Wolfram MathWorld
• Archimedean Spiral Plane Curves
• 螺旋线

标签：阿基米德,曲线,螺旋,JavaScript,螺旋线,螺线,Archimedean,坐标系
来源： https://www.cnblogs.com/thyshare/p/15419109.html