首页 > 其他分享> > Symmetric Cross Entropy for Robust Learning with Noisy Labels 笔记

Symmetric Cross Entropy for Robust Learning with Noisy Labels 笔记

2021-03-13 22:30:30 作者：互联网

SCE笔记

《Symmetric Cross Entropy for Robust Learning with Noisy Labels》

文章目录

SCE笔记

存在的问题

作者通过对DNN训练过程的进一步分析，发现使用CCE损失函数是class-biased的

class-biased: 训练数据中存在着不同的类别，有些类别 (“easy” classes) 的数据学习更容易，收敛速度更快。有些类别(“hard” classes)更加难以学习。

如下图中：

如图所示，在训练的过程中，即使整个数据集是干净的，分类测试的准确率仍存在很大差异。（红色虚线的class3和橙色虚线的class1相差接近20%）

加了噪声后情况更加严重，class3的精度大约只有60%，但是class6的精确度>90。

一种常见的方法就是使用Label Smoothing Regularization (LSR) 标签平滑正则化。下图是使用LSR后的准确率曲线。

可以看出，“hard” classes的准确率仍然很低。

说明，在噪声数据下，模型糟糕的表现不仅仅与过拟合噪声标签有关，还和“hard” classes有关

在噪声数据下，不同的类得到的准确率也不同。

上图是可视化的结果（训练数据集为CIFAR-10，使用 t-SNE 2D在最后一层进行embeddings，加入噪声率为40%的symmetric 噪声标签）

可以看出（a）图干净数据中，聚类的分界更加明显。但是无论干净数据还是噪声数据中，一些聚类的边界更加明显（“easy” classes），一些聚类边界更加模糊（“hard” classes）

提出的方法

受到KL散度的影响，作者提出了一种noise tolerant的方法。将Reverse Cross Entropy (RCE)和CE进行结合，得到对称交叉熵函数Symmetric cross entropy Learning (SL). SL不仅促进了“hard” classes的学习，还提高了DNN对噪声的鲁棒性。

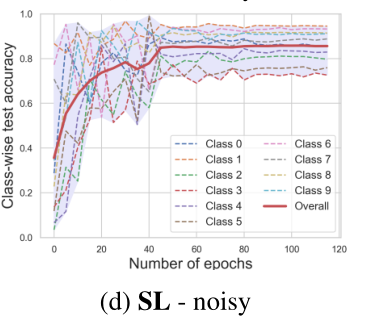
上面两幅图是SL实验的结果，数据集和噪声设置没变。可以看出使用SL，最低的准确率由60%左右提升至了75%。在embedding图上也可以看出，聚类的边界更加明显。

Cross Entropy的局限性

文章在接下来重点分析了CE在噪声标签下存在的问题。

数据集使用的是随机噪声，噪声率40%。网络结构是一个8层的卷积神经网络。

下面这张图像分别选取了学习过程中三个不同的阶段，分别是第10epoch，第50epoch，第100epoch（整个训练过程有120个epoch）

由上图可以看出，在干净数据下，整个学习过程中，每个类之间的准确率都是不一样的。在噪声数据下不同类的准确率也存在着差异。

在噪声数据中，难以学习的类（例如class2/3），经过100个epoch后，准确率与干净数据下的相差20%。说明在噪声数据下，一些难以训练的类别还未得到充分的训练。

而一些容易学习的类（例如class1/6 ），已经出现过拟合的现象。100个epoch下的准确率不如50个epoch。

从上面两图来看，在噪声数据集中，影响准确率的因素有两个，其中“hard” classes未能得到很好的训练带来的影响要比过拟合噪声标签带来的影响要大。

如上图所示，在加了噪声后，class3（红色）基本分散在其他类之中。这会导致对class3进行预测时，被分配到与他相似的类的概率更大。虽然在class3中仍然存在着60%的真实标签，但是class3已经没有明显的聚类。

进一步讨论class3样本中60%的干净部分。下图是class3干净数据部分下的平均置信度。（CIFAR-10数据集，40%噪声）

上图可以看出。即使是干净数据的部分，class3在正确标签下的置信度仍然不是很高，只达到了0.5左右，说明训练的不够充分。

说明CE对于hard classes标签下的学习是不够的，特别是在有噪声的标签下。

SCE的具体做法

定义

对称交叉熵的定义：

有两个分布 p p p和 q q q，交叉熵： H ( q , p ) H(q,p) H(q,p) KL散度： K L ( q ∣ ∣ p ) KL(q||p) KL(q∣∣p)

KL散度的定义：

K L ( q ∥ p ) = H ( q , p ) − H ( q ) K L(q \| p)=H(q, p)-H(q) KL(q∥p)=H(q,p)−H(q)

其中

q = q ( k ∣ x ) q = q(k|x) q=q(k∣x)代表样本的真实分布

p = p ( k ∣ x ) p = p(k|x) p=p(k∣x)代表预测的分布

从KL散度的的角度来看，优化的目的就是使 q = q ( k ∣ x ) q = q(k|x) q=q(k∣x) 和 p = p ( k ∣ x ) p = p(k|x) p=p(k∣x) 越接近越好。也是最小化KL散度。

但是在标签噪声中， q = q ( k ∣ x ) q = q(k|x) q=q(k∣x)不一定代表真实的分布，而 p = p ( k ∣ x ) p = p(k|x) p=p(k∣x)在一定程度上可以反映真实的分布。

所以另一个方向的KL散度 K L ( p ∣ ∣ q ) KL(p||q) KL(p∣∣q)

对称KL散度的公式为：

S K L = K L ( q ∥ p ) + K L ( p ∥ q ) S K L=K L(q \| p)+K L(p \| q) SKL=KL(q∥p)+KL(p∥q)

将这思想转化到交叉熵上，即得出了对称交叉熵公式。

S C E = C E + R C E = H ( q , p ) + H ( p , q ) S C E=C E+R C E=H(q, p)+H(p, q) SCE=CE+RCE=H(q,p)+H(p,q)

其中：REC： ℓ r c e = − ∑ k = 1 K p ( k ∣ x ) log ⁡ q ( k ∣ x ) \ell_{r c e}=-\sum_{k=1}^{K} p(k \mid \mathbf{x}) \log q(k \mid \mathbf{x}) ℓrce=−∑k=1Kp(k∣x)logq(k∣x)

所以损失函数的定义为： ℓ s c e = ℓ c e + ℓ r c e \ell_{s c e}=\ell_{c e}+\ell_{r c e} ℓsce=ℓce+ℓrce

虽然RCE是noise tolerant的，但是CE不是鲁棒的噪声函数。因此提出了两个参数，α和β

α解决CE的过拟合问题，β用于探究RCE的鲁棒性

ℓ s l = α ℓ c e + β ℓ r c e \ell_{s l}=\alpha \ell_{c e}+\beta \ell_{r c e} ℓsl=αℓce+βℓrce

在 ℓ r c e \ell_{r c e} ℓrce中，因为标签分布是one-hot编码，含有0的值。为了解决这一个问题，作者定义了 l o g 0 = A log0 = A log0=A (A是小于零，的一个常数）

其中 β \beta β 对RCE的影响也和A的值有关。

鲁棒性分析

数据集： x x x，噪声标签： y ^ \hat{y} y^，真实标签： y y y

干净标签的风险： R ( f ) = E x , y ℓ r c e R(f)=\mathbb{E}_{\mathbf{x}, y} \ell_{r c e} R(f)=Ex,yℓrce ，噪声标签的风险： R η ( f ) = E x , y ^ ℓ r c e R^{\eta}(f)=\mathbb{E}_{\mathbf{x}, \hat{y}} \ell_{r c e} Rη(f)=Ex,y^ℓrce

f ∗ f^{*} f∗ and f η ∗ f_{\eta}^{*} fη∗ 是 R ( f ) R(f) R(f) and R η ( f ) R^{\eta}(f) Rη(f)的全局最小化

如果 f ∗ f^{*} f∗ 和 f η ∗ f_{\eta}^{*} fη∗在噪声数据下，有着相同的分类概率。可以说该损失函数是noise-tolerant的。

证明过程：

在多分类的问题中，如果噪声率 η < 1 − 1 K \eta<1-\frac{1}{K} η<1−K1， ℓ r c e \ell_{r c e} ℓrce在对称或者均匀噪声标签下是noise tolerant 。如果 R ( f ∗ ) = 0 R\left(f^{*}\right)=0 R(f∗)=0， ℓ r c e \ell_{r c e} ℓrce在噪声率 η y k < 1 − η y \eta_{y k}<1-\eta_{y} ηyk<1−ηy with ∑ k ≠ y η y k = η y \sum_{k \neq y} \eta_{y k}=\eta_{y} ∑k=yηyk=ηy 的asymmetric or class-dependent 标签下，也是noise tolerant的。

在对称噪声下：

R η ( f ) = E x , y ^ ℓ r c e = E x E y ∣ x E y ^ ∣ x , y ℓ r c e = E x E y ∣ x [ ( 1 − η ) ℓ r c e + η K − 1 ∑ k ≠ y K ℓ r c e ] = ( 1 − η ) R ( f ) + η K − 1 ( ∑ k = 1 K ℓ r c e − R ( f ) ) = R ( f ) ( 1 − η K K − 1 ) − A η \begin{aligned} R^{\eta}(f) &=\mathbb{E}_{\mathbf{x}, \hat{y}} \ell_{r c e}=\mathbb{E}_{\mathbf{x}} \mathbb{E}_{y \mid \mathbf{x}} \mathbb{E}_{\hat{y} \mid \mathbf{x}, y} \ell_{r c e} \\ &=\mathbb{E}_{\mathbf{x}} \mathbb{E}_{y \mid \mathbf{x}}\left[(1-\eta) \ell_{r c e}+\frac{\eta}{K-1} \sum_{k \neq y}^{K} \ell_{r c e}\right] \\ &=(1-\eta) R(f)+\frac{\eta}{K-1}\left(\sum_{k=1}^{K} \ell_{r c e}-R(f)\right) \\ &=R(f)\left(1-\frac{\eta K}{K-1}\right)-A \eta \end{aligned} Rη(f)=Ex,y^ℓrce=ExEy∣xEy^∣x,yℓrce=ExEy∣x⎣⎡(1−η)ℓrce+K−1ηk=y∑Kℓrce⎦⎤=(1−η)R(f)+K−1η(k=1∑Kℓrce−R(f))=R(f)(1−K−1ηK)−Aη

其中： ∑ k = 1 K ℓ r c e = − ( K − 1 ) \sum_{k=1}^{K} \ell_{r c e}=-(K-1) ∑k=1Kℓrce=−(K−1)

因此： R η ( f ∗ ) − R η ( f ) = ( 1 − η K K − 1 ) ( R ( f ∗ ) − R ( f ) ) ≤ 0 R^{\eta}\left(f^{*}\right)-R^{\eta}(f)=\left(1-\frac{\eta K}{K-1}\right)\left(R\left(f^{*}\right)-R(f)\right) \leq 0 Rη(f∗)−Rη(f)=(1−K−1ηK)(R(f∗)−R(f))≤0

因为 η < 1 − 1 K \eta<1-\frac{1}{K} η<1−K1， f ∗ f^{*} f∗是 R ( f ) R(f) R(f) 的全局最小化。上述方程证明了 f ∗ f^{*} f∗也是 R η ( f ) R^{\eta}(f) Rη(f)的全局最小化。因此 ℓ r c e \ell_{r c e} ℓrce是noise tolerant 的。

梯度分析

下面分析SL损失的梯度，令 α , β = 1 \alpha,\beta = 1 α,β=1

对SL进行求导:

∂ ℓ s l ∂ z j = − ∑ k = 1 K q k 1 p k ∂ p k ∂ z j − ∑ k = 1 K ∂ p k ∂ z j log ⁡ q k \frac{\partial \ell_{s l}}{\partial z_{j}}=-\sum_{k=1}^{K} q_{k} \frac{1}{p_{k}} \frac{\partial p_{k}}{\partial z_{j}}-\sum_{k=1}^{K} \frac{\partial p_{k}}{\partial z_{j}} \log q_{k} ∂zj∂ℓsl=−∑k=1Kqkpk1∂zj∂pk−∑k=1K∂zj∂pklogqk （1）

其中： ∂ p k ∂ z j = ∂ ( e z k ∑ j = 1 K e z j ) ∂ z j = ∂ e z k ∂ z j ( ∑ j = 1 K e z j ) − e z k ∂ ( ∑ j = 1 K e z j ) ∂ z j ( ∑ j = 1 K e z j ) 2 \frac{\partial p_{k}}{\partial z_{j}}=\frac{\partial\left(\frac{e^{z_{k}}}{\sum_{j=1}^{K} e^{z_{j}}}\right)}{\partial z_{j}}=\frac{\frac{\partial e^{z_{k}}}{\partial z_{j}}\left(\sum_{j=1}^{K} e^{z_{j}}\right)-e^{z_{k}} \frac{\partial\left(\sum_{j=1}^{K} e^{z_{j}}\right)}{\partial z_{j}}}{\left(\sum_{j=1}^{K} e^{z_{j}}\right)^{2}} ∂zj∂pk=∂zj∂(∑j=1Kezjezk)=(∑j=1Kezj)2∂zj∂ezk(∑j=1Kezj)−ezk∂zj∂(∑j=1Kezj) （2）

进一步化简得到：

∂ p k ∂ z j = { p k ( 1 − p k ) , k = j − p j p k , k ≠ j \frac{\partial p_{k}}{\partial z_{j}}=\left\{\begin{array}{ll}p_{k}\left(1-p_{k}\right), & k=j \\ -p_{j} p_{k}, & k \neq j\end{array}\right. ∂zj∂pk={pk(1−pk),−pjpk,k=jk=j （3）

由公式1和公式3可以得到：

∂ ℓ s l ∂ z j = − ∑ k = 1 K q k 1 p k ∂ p k ∂ z j − ∑ k = 1 K ∂ p k ∂ z j log ⁡ q k = − ∑ k ≠ j K q k p k ( − p j p k ) − q j p j ( p j ( 1 − p j ) ) − ∑ k ≠ j K ( − p j p k ) log ⁡ q k − p j ( 1 − p j ) log ⁡ q j \begin{aligned} \frac{\partial \ell_{s l}}{\partial z_{j}} &=-\sum_{k=1}^{K} q_{k} \frac{1}{p_{k}} \frac{\partial p_{k}}{\partial z_{j}}-\sum_{k=1}^{K} \frac{\partial p_{k}}{\partial z_{j}} \log q_{k} \\ &=-\sum_{k \neq j}^{K} \frac{q_{k}}{p_{k}}\left(-p_{j} p_{k}\right)-\frac{q_{j}}{p_{j}}\left(p_{j}\left(1-p_{j}\right)\right)-\sum_{k \neq j}^{K}\left(-p_{j} p_{k}\right) \log q_{k}-p_{j}\left(1-p_{j}\right) \log q_{j} \end{aligned} ∂zj∂ℓsl=−k=1∑Kqkpk1∂zj∂pk−k=1∑K∂zj∂pklogqk=−k=j∑Kpkqk(−pjpk)−pjqj(pj(1−pj))−k=j∑K(−pjpk)logqk−pj(1−pj)logqj （4）

推导出：

∂ ℓ s l ∂ z j = { ∂ ℓ c e ∂ z j − ( A p j 2 − A p j ) , q j = q y = 1 ∂ ℓ c e ∂ z j + ( − A p j p y ) , q j = 0 \frac{\partial \ell_{s l}}{\partial z_{j}}=\left\{\begin{array}{ll}\frac{\partial \ell_{c e}}{\partial z_{j}}-\left(A p_{j}^{2}-A p_{j}\right), & q_{j}=q_{y}=1 \\ \frac{\partial \ell_{c e}}{\partial z_{j}}+\left(-A p_{j} p_{y}\right), & q_{j}=0\end{array}\right. ∂zj∂ℓsl={∂zj∂ℓce−(Apj2−Apj),∂zj∂ℓce+(−Apjpy),qj=qy=1qj=0

其中 A A A用来代替 l o g 0 log0 log0

其中CE损失的梯度：

∂ ℓ c e ∂ z j = { p j − 1 ≤ 0 , q j = q y = 1 p j ≥ 0 , q j = 0 \frac{\partial \ell_{c e}}{\partial z_{j}}=\left\{\begin{array}{ll}p_{j}-1 \leq 0, & q_{j}=q_{y}=1 \\ p_{j} \geq 0, & q_{j}=0\end{array}\right. ∂zj∂ℓce={pj−1≤0,pj≥0,qj=qy=1qj=0

由梯度公式可以看出：

当 q j = q y = 1 q_{j}=q_{y}=1 qj=qy=1，（样本属于j类）， ∂ ℓ c e ∂ z j ≤ 0 \frac{\partial \ell_{c e}}{\partial z_{j}} \leq 0 ∂zj∂ℓce≤0 ，公式的第二项， A p j 2 − A p j A p_{j}^{2}-A p_{j} Apj2−Apj的值却决于 p j p_j pj

A p j 2 − A p j A p_{j}^{2}-A p_{j} Apj2−Apj 是在第二象限的凸抛物线。其中 p j ∈ [ 0 , 1 ] p_j \in [0,1] pj∈[0,1]，且在0.5时取到峰值。

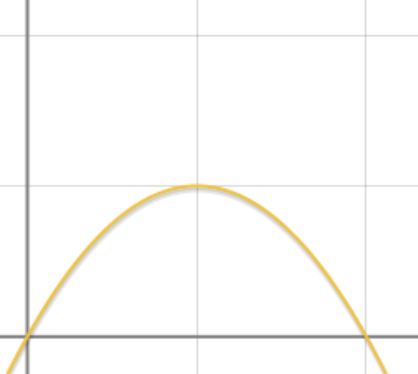
学习过程的目标是使 p j → 1 p_{j} \rightarrow 1 pj→1，当 p j < 0.5 p_j < 0.5 pj<0.5时，RCE项会促进学习。当 p j > 0.5 p_j > 0.5 pj>0.5时，RCE项会降低样本的学习速度。

当 q j = 0 ( ∂ ℓ c e ∂ z i ≥ 0 ) q_{j}=0\left(\frac{\partial \ell_{c e}}{\partial z_{i}} \geq 0\right) qj=0(∂zi∂ℓce≥0)时，（其他类），公式第二项 − A p j p y -A p_{j} p_{y} −Apjpy ，取决于 p i p_i pi和 p y p_y py（模型对正确分类的信任程度）。

p y p_y py越大，说明模型越信任自己的预测，同时 − A p j p y -A p_{j} p_{y} −Apjpy也越大。其他标签的预测概率的下降速度就越快。

p y = 0 p_y = 0 py=0， − A p j p y = 0 -A p_{j} p_{y} = 0 −Apjpy=0梯度的大小没有改变，说明网络对自己预测没有信心，则标签可能是错误的。

RCE和MAE

改变CE梯度的最简单的方法就是在公式前面加上一个系数，例如（“2CE，5CE”）。但是这会导致对数据的过拟合。如下图

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-SBcDAbcF-1615644927325)(https://i.loli.net/2020/10/14/MNlwqTfSi7nkueV.png)]

研究发现，MAE是RCE中A = -2 的特例。证明如下：

MAE公式推导：

ℓ mae = ∑ k = 1 K ∣ p ( k ∣ x ) − q ( k ∣ x ) ∣ = ( 1 − p ( y ∣ x ) ) + ∑ k ≠ y p ( k ∣ x ) = 2 ( 1 − p ( y ∣ x ) ) \begin{aligned} \ell_{\text {mae}} &=\sum_{k=1}^{K}|p(k \mid \mathbf{x})-q(k \mid \mathbf{x})|=(1-p(y \mid \mathbf{x}))+\sum_{k \neq y} p(k \mid \mathbf{x}) \\ &=2(1-p(y \mid \mathbf{x})) \end{aligned} ℓmae=k=1∑K∣p(k∣x)−q(k∣x)∣=(1−p(y∣x))+k=y∑p(k∣x)=2(1−p(y∣x))

对于RCE

ℓ r c e = − ∑ k = 1 K p ( k ∣ x ) log ⁡ q ( k ∣ x ) = − p ( y ∣ x ) log ⁡ 1 − ∑ k ≠ y p ( k ∣ x ) A = − A ∑ k ≠ y p ( k ∣ x ) = − A ( 1 − p ( y ∣ x ) ) \begin{aligned} \ell_{r c e} &=-\sum_{k=1}^{K} p(k \mid \mathbf{x}) \log q(k \mid \mathbf{x}) \\ &=-p(y \mid \mathbf{x}) \log 1-\sum_{k \neq y} p(k \mid \mathbf{x}) A=-A \sum_{k \neq y} p(k \mid \mathbf{x}) \\ &=-A(1-p(y \mid \mathbf{x})) \end{aligned} ℓrce=−k=1∑Kp(k∣x)logq(k∣x)=−p(y∣x)log1−k=y∑p(k∣x)A=−Ak=y∑p(k∣x)=−A(1−p(y∣x))

也就是说，当A = -2时，RCE简化为了MAE。

可以说RCE是MAE的推广

不同于GCE，SL包含了两个对称的学习项。

实验

实验准备

数据集：MNIST, CIFAR-10, CIFAR-100, and a large-scale real-world noisy dataset Clothing1M.

**噪声的设置方法：**加入了两种噪声

symmetric (uniform) noise ：将等比例的标签转换为其他标签。
asymmetric (class-dependent) noise：在一些特定标签之中进行转换。

MNIST中，2 → 7, 3 → 8, 5 ↔ 6 ,7 → 1。

CIFAR-10中：TRUCK → AUTOMOBILE, BIRD → AIRPLANE,DEER → HORSE, CAT ↔ DOG;

CIFAR-100中：100个分类被分成了20个大类，每个大类中有5个子类。然后在每个大类中随机选择两个子类切换。

实验验证

实验设置：

使用8层CNN网络（6个卷积层，2个全连接层）。

使用SGD（momentum 0.9，weight decay 1 0 − 4 10^{-4} 10−4，初始学习率：0.01，在40和80个epoch之后除以10，共120个epoch）

参数 α , β , A \alpha , \beta, A α,β,A分别设置为0.1，1，-6

类标签的学习

在40%的噪声数据和60%的噪声数据下，分别使用CE和SL进行训练，结果如下：

40%噪声下：
60%噪声下

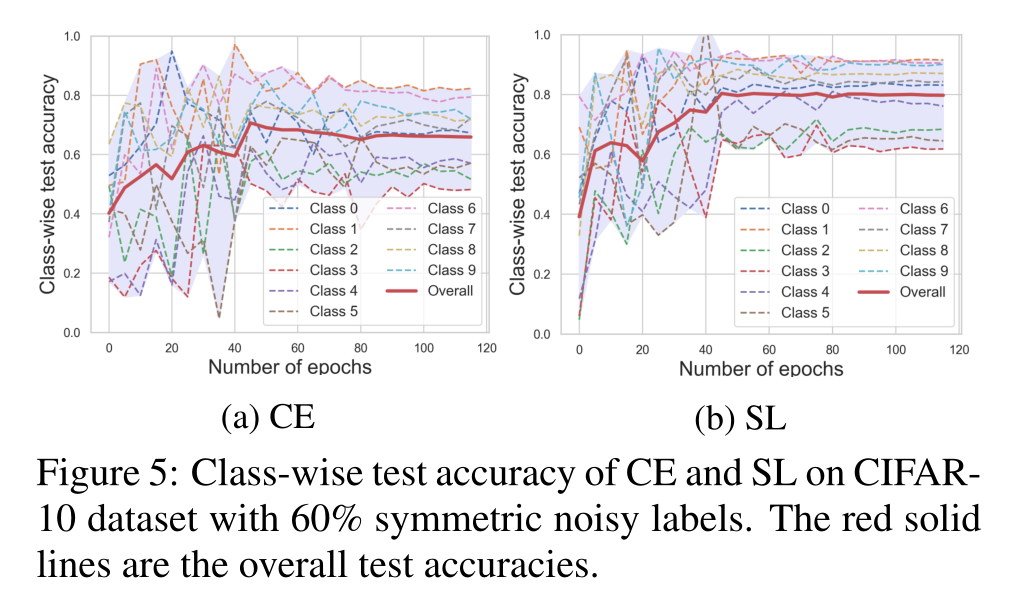
可以看出，在两种噪声数据中，SL都比CE更充分地学了每一个类，并且准确率也有所提升。尤其是那些难度较大的类，例如class2、3、4、5，SL显著地提升了他们的学习表现。

这是因为SL通过自适应的学习速度，来鼓励在hard - class中进行学习。

在学习的过程中，easy class可以更快地学习到高的概率 p k > 0.5 p_k > 0.5 pk>0.5，但是hard class学习到的概率仍然很低 p k < 0.5 p_k < 0.5 pk<0.5。SL可以控制他们的平衡，降低 p k > 0.5 p_k > 0.5 pk>0.5样本的学习速度，增加 p k < 0.5 p_k < 0.5 pk<0.5样本的学习速度.