浅谈WQS二分
作者:互联网
前言
确实是浅谈。
讲解
应用领域
WQS二分用于解决形似于有限制地恰好选 \(x\) 个物品,使其权值和最大或最小。
而且随着选物品个数的增多,这个权值呈一个凸函数的形式。
原理
考虑一下如果不是必须选 \(x\) 个而是随便选怎么做?
其实对于每道题都不一样,但一定都很好求出来,这是WQS二分题的一个特点。
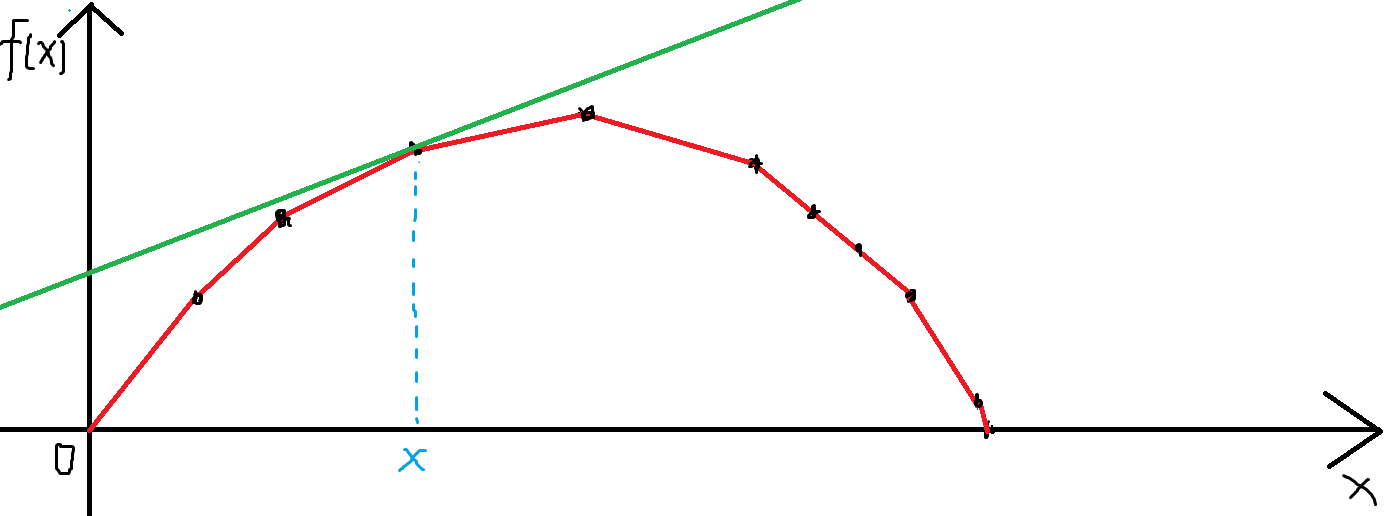
我们令选的物品个数为横坐标,权值为纵坐标建立一个平面直角坐标系。
人傻图丑,见谅。
如果我们要找到 \(x\) 对应的这个点怎么做?
考虑寻找一个斜率为 \(k\) 的直线去切这个凸包,如果这条直线刚好切到这个点就搞定了,显然此时的这个点的截距b最大。
如图:
但是这代表什么呢?我们要求的答案就是 \(kx+b\)啊!
我们只需要对每个物品的权值都减去 \(k\)(似乎很多博客里面都是加,但是我觉得减应该更好理解),然后任意选,如果刚好选出 \(x\) 个,选出来的权值是 \(b\),那么我们的答案就是 \(kx+b\)。
而这个找斜率 \(k\) 的过程,我们用二分实现。
但是细心的你一定发现了一个问题,如果一条直线切到了很多点怎么办?
我们现在只能找到 \(x_1\) 或者 \(x_2\)对应的函数值了,怎么办?
已经足够了。
假设我们找到了 \(x_2\) (个人喜好),我们需要的权值是:\(kx+b\),而我们找到的是 \(kx_2+b\)。
诶?!斜率一样,我们直接把 \(x_2\) 换成 \(x\) 不就行了!反正他们共用一个斜率 \(k\),而且我们已经找到了。
练习
例1
我们只需给白边加上斜率 \(k\) 跑 \(Kruskal\) 即可,板题。
如果你按照我的喜好来实现这份代码,也就是说斜率相等的时候选择 \(x_2\),那么你应该在白边与黑边权值相等的时候优先选白边,这样才能找到 \(x_2\)。
当然你如果优先选白边,那么你就会得到 \(x_1\)。
思考:
如何严格实现 \(m\log_2m\) 而不是 \(m\log_2^2m\)。
答案:
对白边和黑边分别按权值排序,白边统一加上 \(k\) 之后也不会改变其大小顺序,用 \(\tt two\ pointers\) 即可。
例2
代码
例1
struct edge
{
int u,v,val;
edge(){}
edge(int u1,int v1,int val1){
u = u1;
v = v1;
val = val1;
}
bool operator < (const edge &px)const{
return val < px.val;
}
}w[MAXM],b[MAXM];
int f[MAXN];
int findSet(int x){if(f[x] != x) f[x] = findSet(f[x]);return f[x];}
bool unionSet(int x,int y)
{
int u = findSet(x),v = findSet(y);
if(u == v) return 0;
f[u] = v; return 1;
}
int solve(int x)
{
for(int i = 1;i <= n;++ i) f[i] = i;
int bn = 1,wn = 1,ret = 0,cnt = 1; ans = 0;
while(cnt < n)
{
if(bn > btot || w[wn].val - x <= b[bn].val)
{
if(unionSet(w[wn].u,w[wn].v)) cnt++,ret++,ans += w[wn].val - x;
wn++;
}
else
{
if(unionSet(b[bn].u,b[bn].v)) cnt++,ans += b[bn].val;
bn++;
}
}
return ret;
}
int main()
{
// freopen("P2619_6.in","r",stdin);
// freopen(".out","w",stdout);
n = Read(); m = Read(); nd = Read();
for(int i = 1,u,v,val;i <= m;++ i)
{
u = Read()+1,v = Read()+1,val = Read();
if(Read()) b[++btot] = edge(u,v,val);
else w[++wtot] = edge(u,v,val);
}
sort(b+1,b+btot+1); sort(w+1,w+wtot+1);
int l = -100,r = 100,ret = 100;
while(l <= r)
{
int mid = (l+r) / 2;
if(solve(mid) >= nd) r = mid-1,ret = mid;
else l = mid+1;
}
solve(ret);
Put(ans + nd * ret);
return 0;
}
例2
相信聪明的读者一定会自己写出来的,加油!
小结
其实WQS二分的思路并不难懂,无论是严格证明还是感性理解都比较容易,只是它的边界需要仔细思考。
标签:二分,return,浅谈,val,int,白边,WQS,斜率,权值 来源: https://www.cnblogs.com/PPLPPL/p/14527614.html