Codeforces 559E - Gerald and Path（dp）

题面传送门

真·难度 *3000 的 D1E hb 跟我们说“做不出来不太应该”。

首先我们将所有线段按 \(a_i\) 从小到大排序，一个很显然的想法是 \(dp_{i,j,d}\) 表示我们已经钦定了前 \(i\) 个线段的方向，其中右端点最靠右的线段为 \(j\)，它的方向为 \(d\) 所覆盖的最大长度是多少。

接下来考虑转移，考虑从 \(i\) 转移到 \(i+1\)，那么线段 \(i+1\) 覆盖 \(j\) 与 \(i+1\) 中间的部分的长度就是 \(\min(\text{线段}\ i+1\ \text{的右端点}-\text{线段}\ j\ \text{的右端点},\text{线段}\ i+1\ \text{的长度})\)。

但是我们这样计算线段 \(i+1\) 的贡献是错误的，因为可能会出现以下的情况：

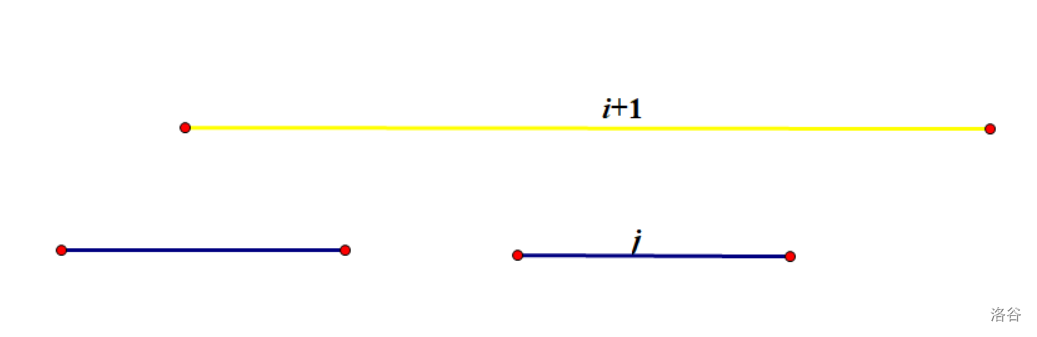
这种情况下贡献是无法直接计算的。不过我们注意到在这种情况下线段 \(j\) 被完全包含在线段 \(i\) 中，也就是说线段 \(j\) 的贡献为 \(0\)。于是我们考虑另一种转移方式：枚举下一个被计入贡献的线段 \(k\)，直接忽略线段 \([i+1,k-1]\) 的贡献。然后按照上面的方式计算即可——虽然我们知道可能 \([i+1,k-1]\) 中的线段也会产生贡献，也就是说我们算出来的贡献不一定是真正的贡献。但是我们清楚，我们忽略了这些贡献，所得到的答案一定没有标准来得更优，并且最优方案一定会被我们考虑到，所以我们这样计算贡献也是正确的。

回到本题来，我们这样计算其实还会忽略一种贡献，那就是在 \([i+1,k-1]\) 中右端点最靠右的线段 \(j\) 的右端点超过了 \(k\) 的右端点，那这样还会产生 \(\text{线段}\ j\ \text{的右端点}-\text{线段}\ k\ \text{的右端点}\) 的贡献，如下图所示：

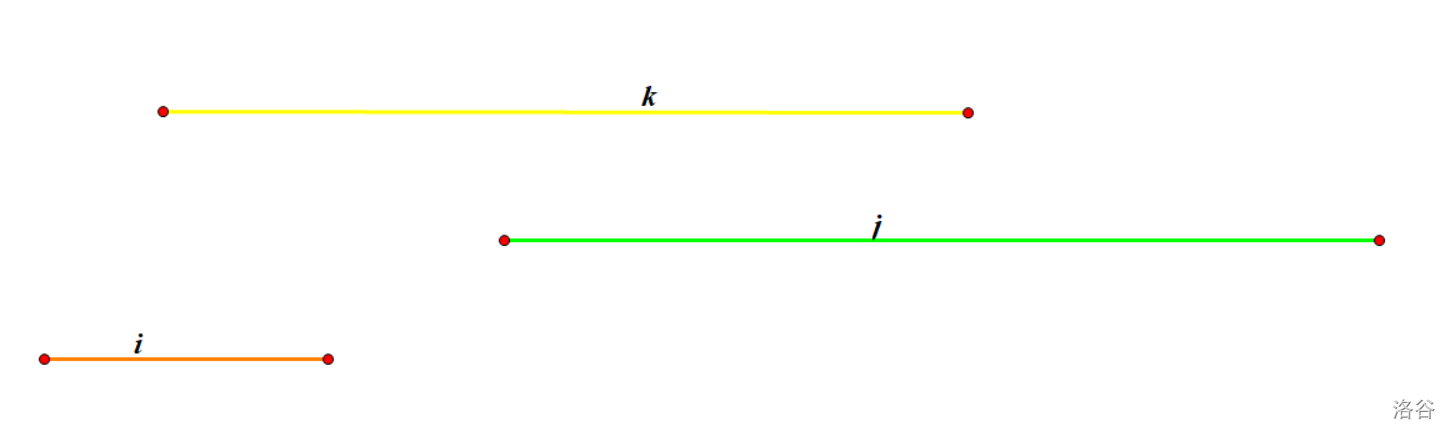
也就是说，对于 \([i+1,k-1]\) 的线段，我们贪心地钦定每个线段都朝右（我们假设这些线段朝左都没有贡献了），然后看是否存在某条线段右端点超过 \(k\)。

具体来说，我们枚举 \(k\in [i+1,n]\)，以及 \(k\) 的方向 \(d_k\)，然后在枚举的过程中，记录下右端点最大的线段编号 \(r\)，方向 \(d_r\)。然后 \(\mathcal O(1)\) 从 \(dp_{i,j,d}\) 转移到 \(dp_{k,r,d_r}\)，那么它产生的贡献就是 \(\text{线段}\ r\ \text{的右端点}-\text{线段}\ k\ \text{的右端点}+\min(\text{线段}\ k\ \text{的右端点}-\text{线段}\ j\ \text{的右端点},\text{线段}\ k\ \text{的长度})\)。

时间复杂度 \(\mathcal O(n^3)\)

代码戳这儿

标签：Gerald,线段,Codeforces,贡献,559E,端点,text,我们,dp
来源： https://www.cnblogs.com/ET2006/p/Codeforces-559E.html