数据结构——B-树

这个笔记为B树自在人心，看不懂，我当场把这个树吃掉！的概括.

概念

B-树可以理解为平衡二叉树的拓展, 它也是平衡的, 但是每个节点可以有多个关键字. 'B' 后面的 '-' 不是减号.

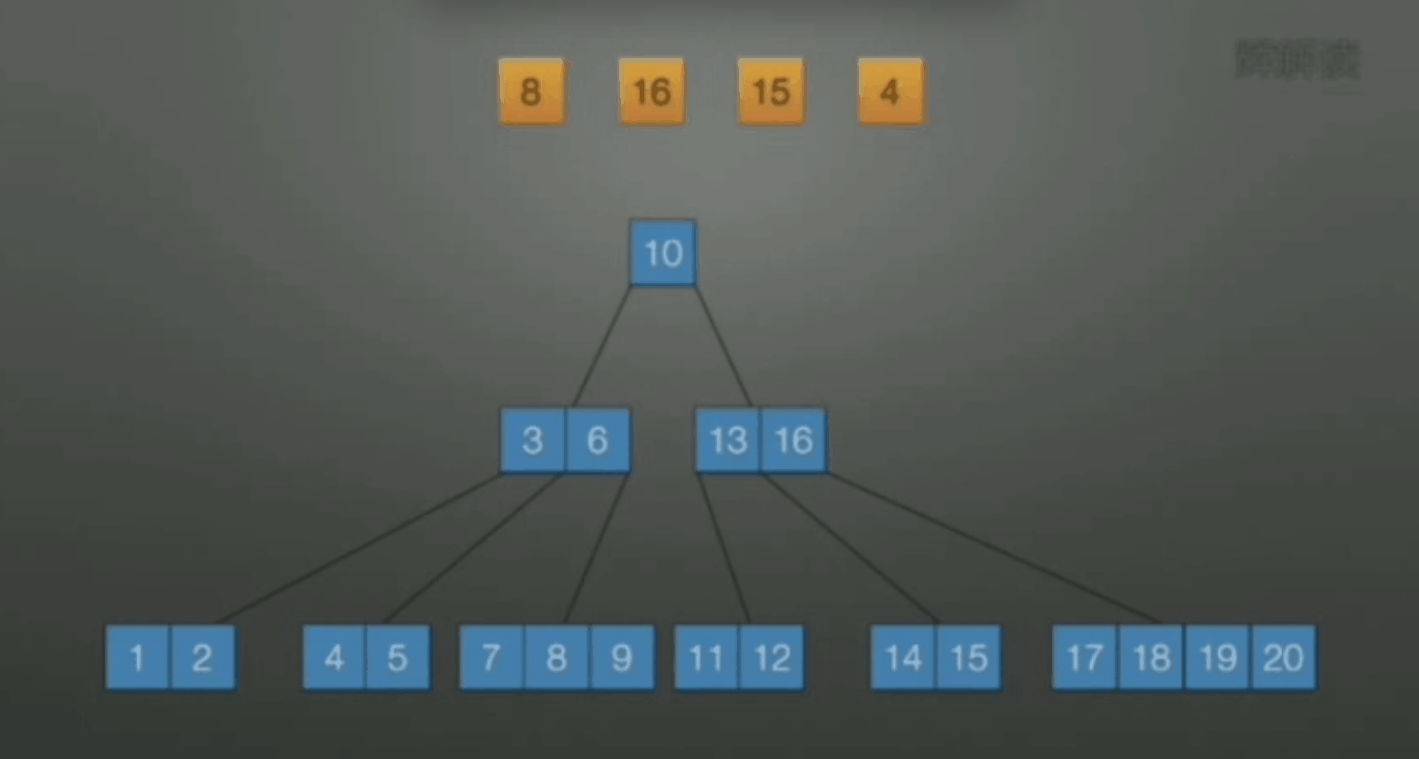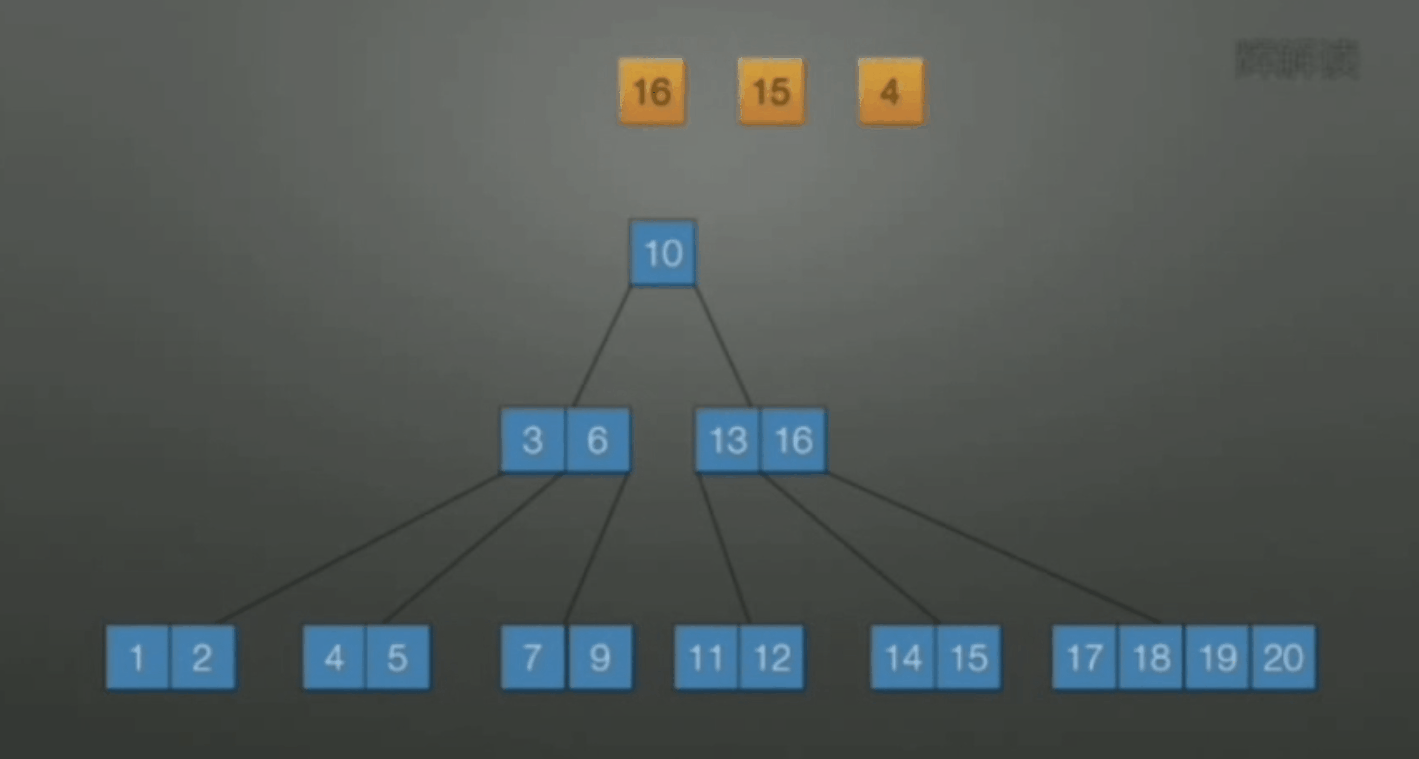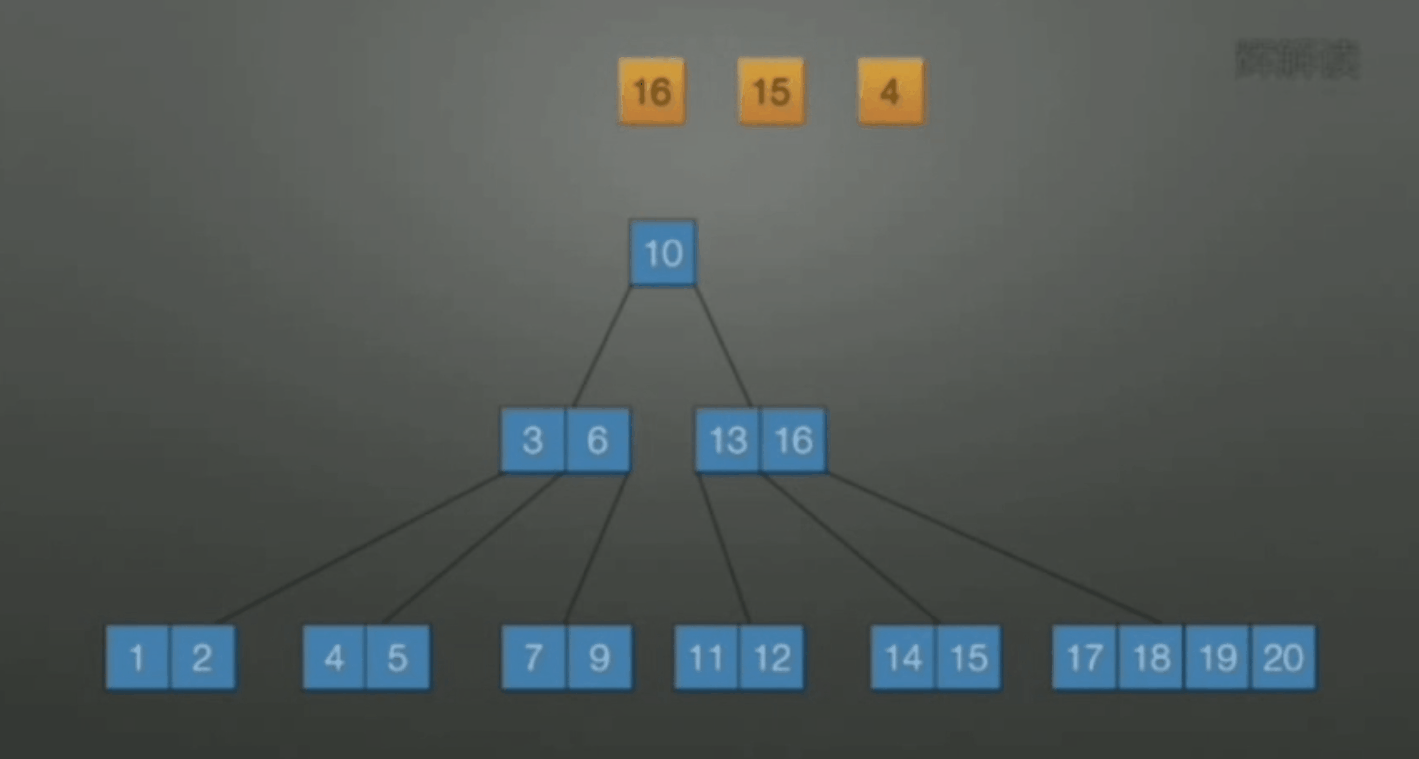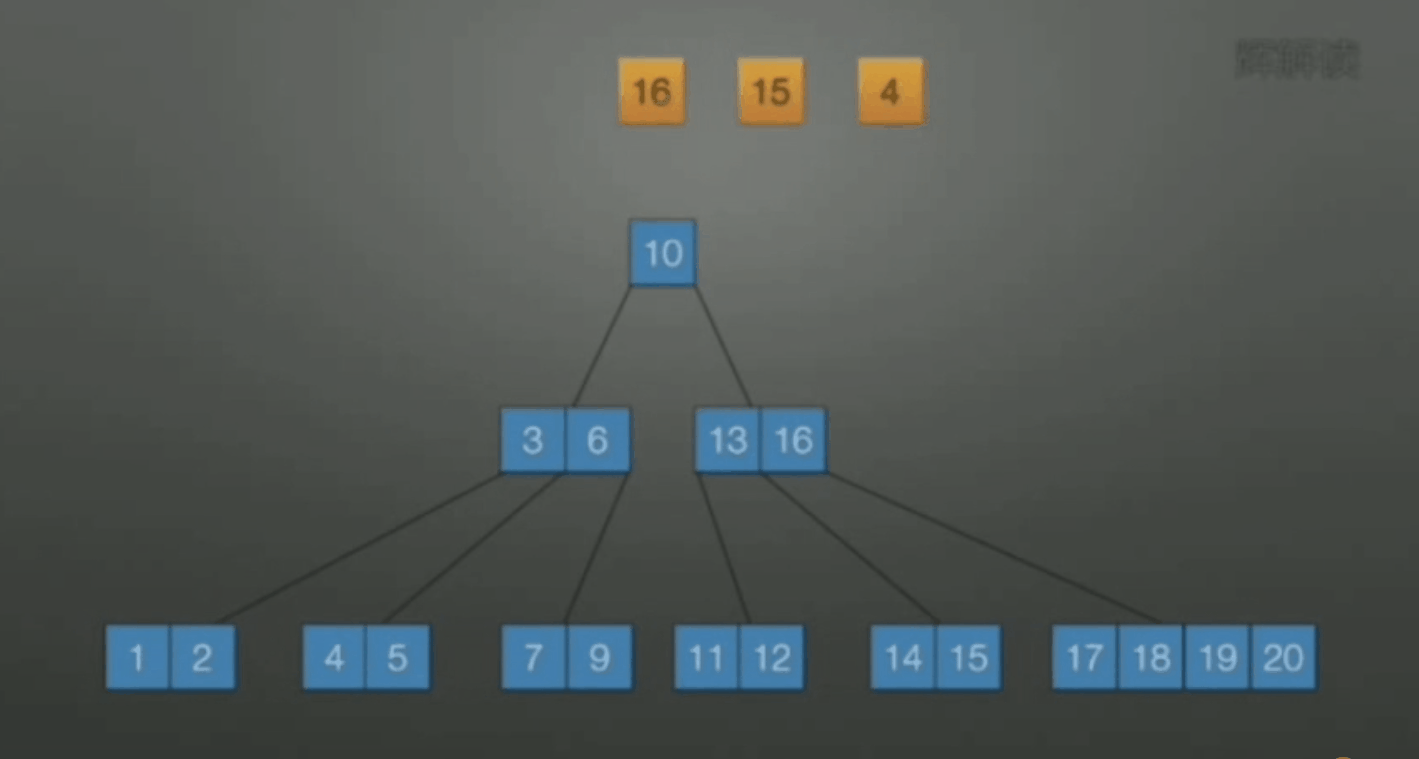
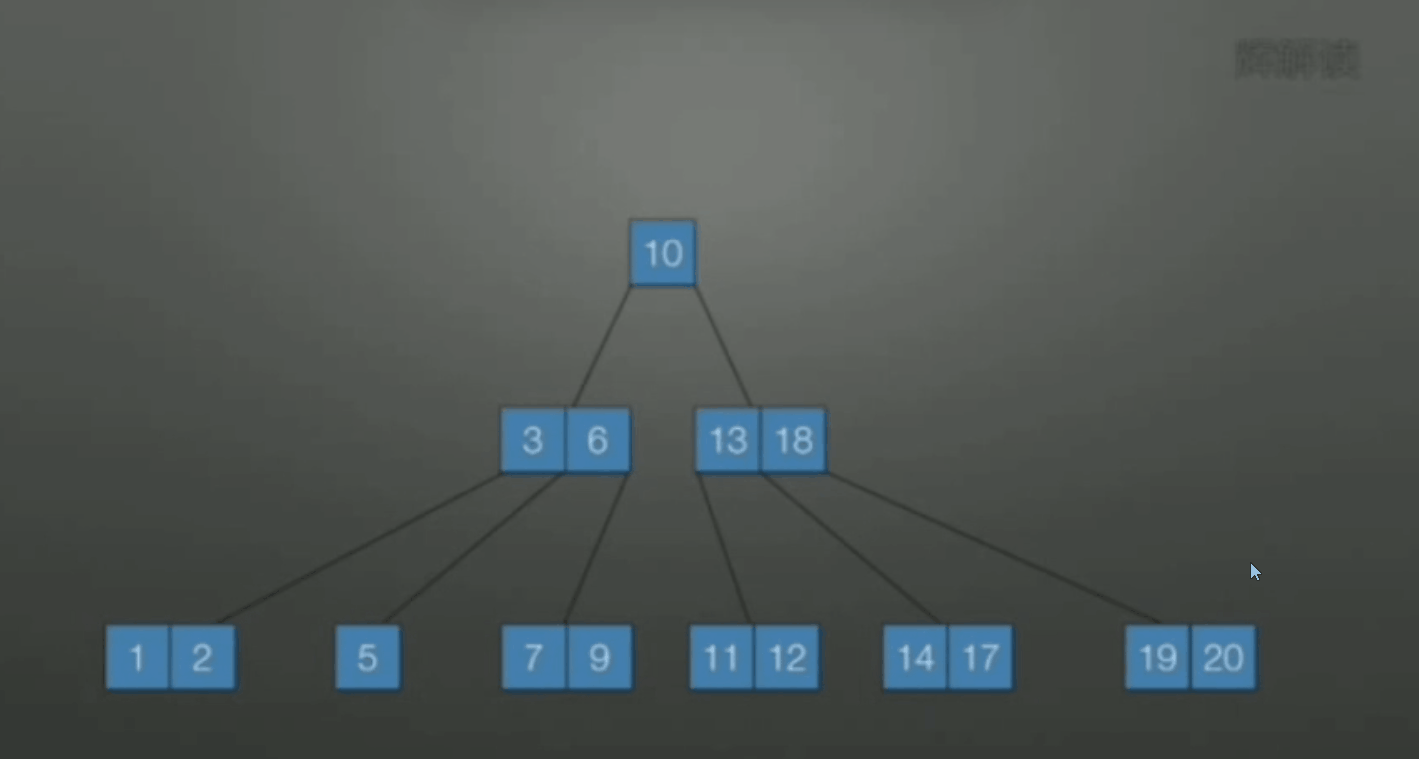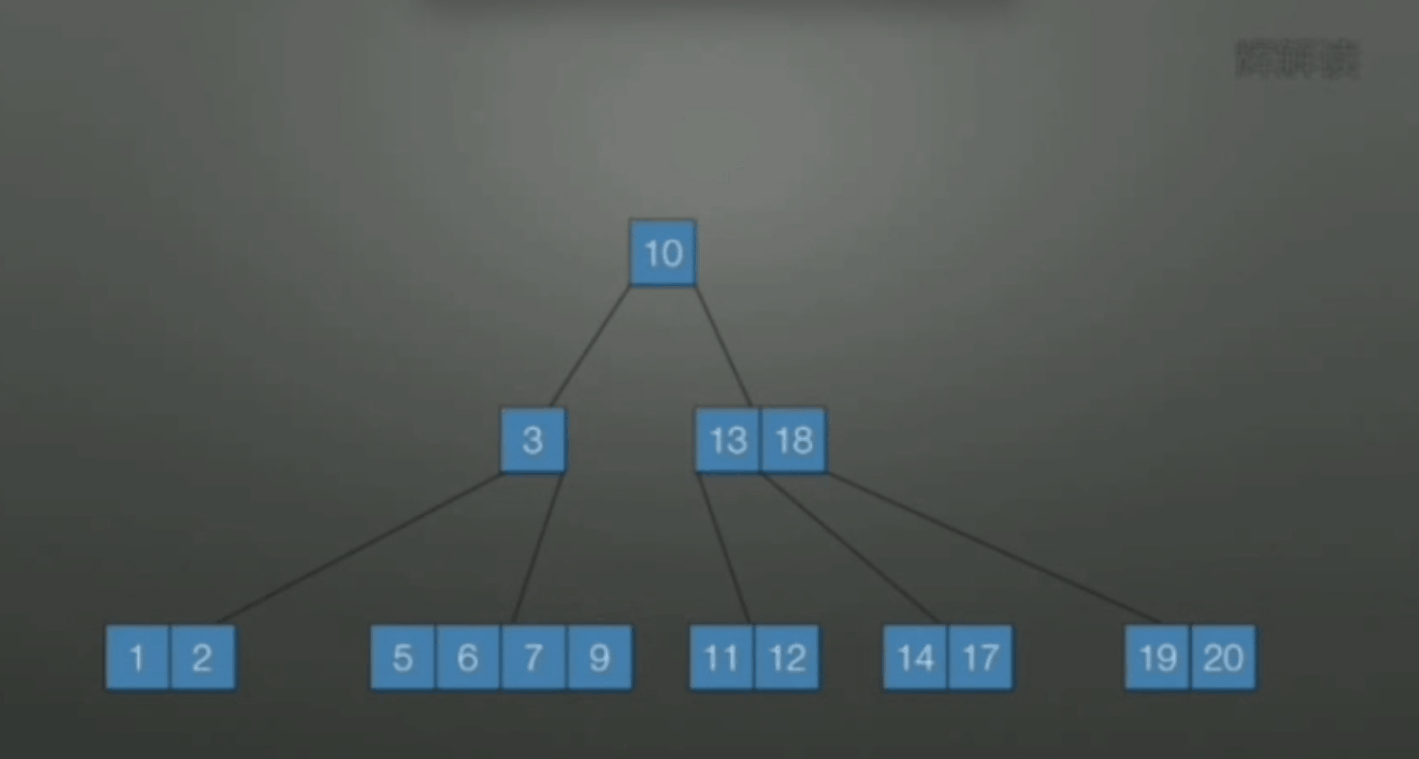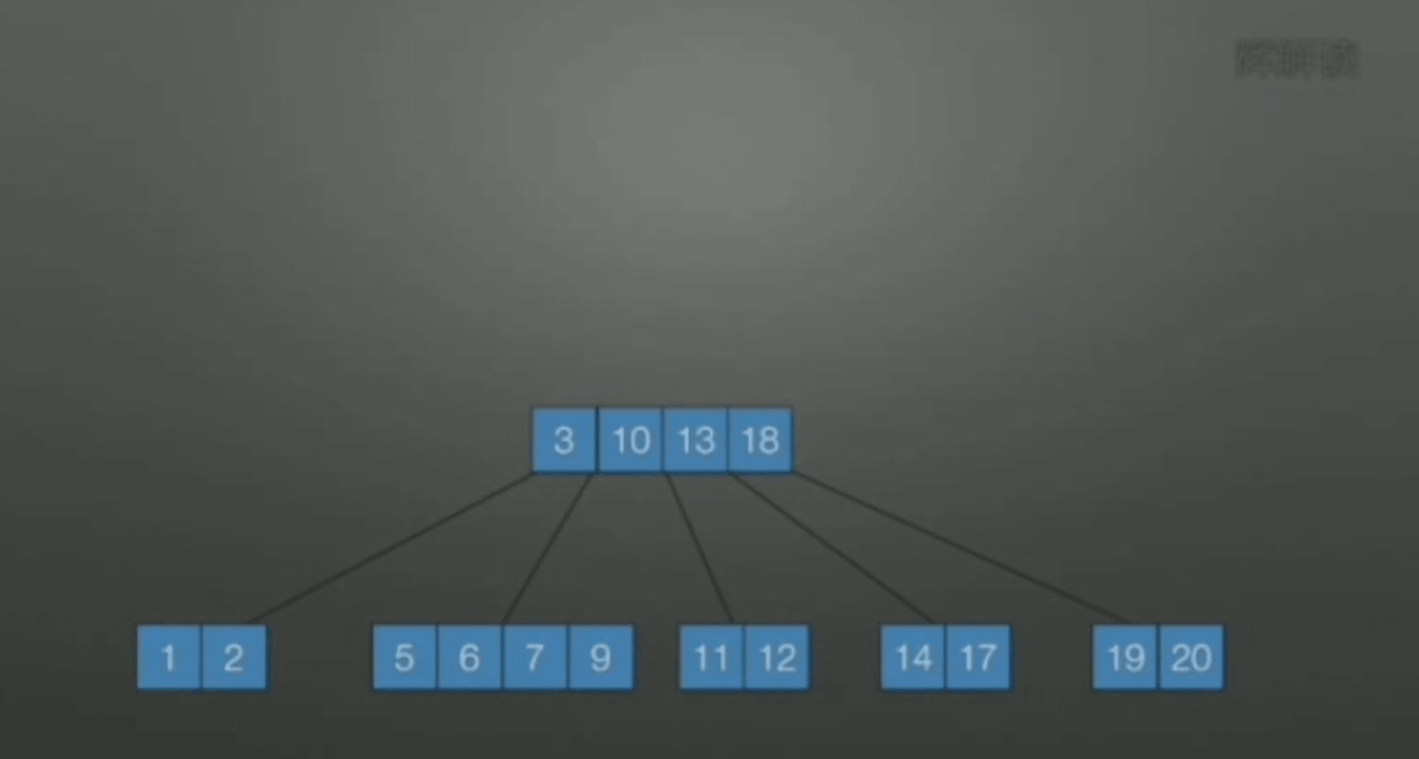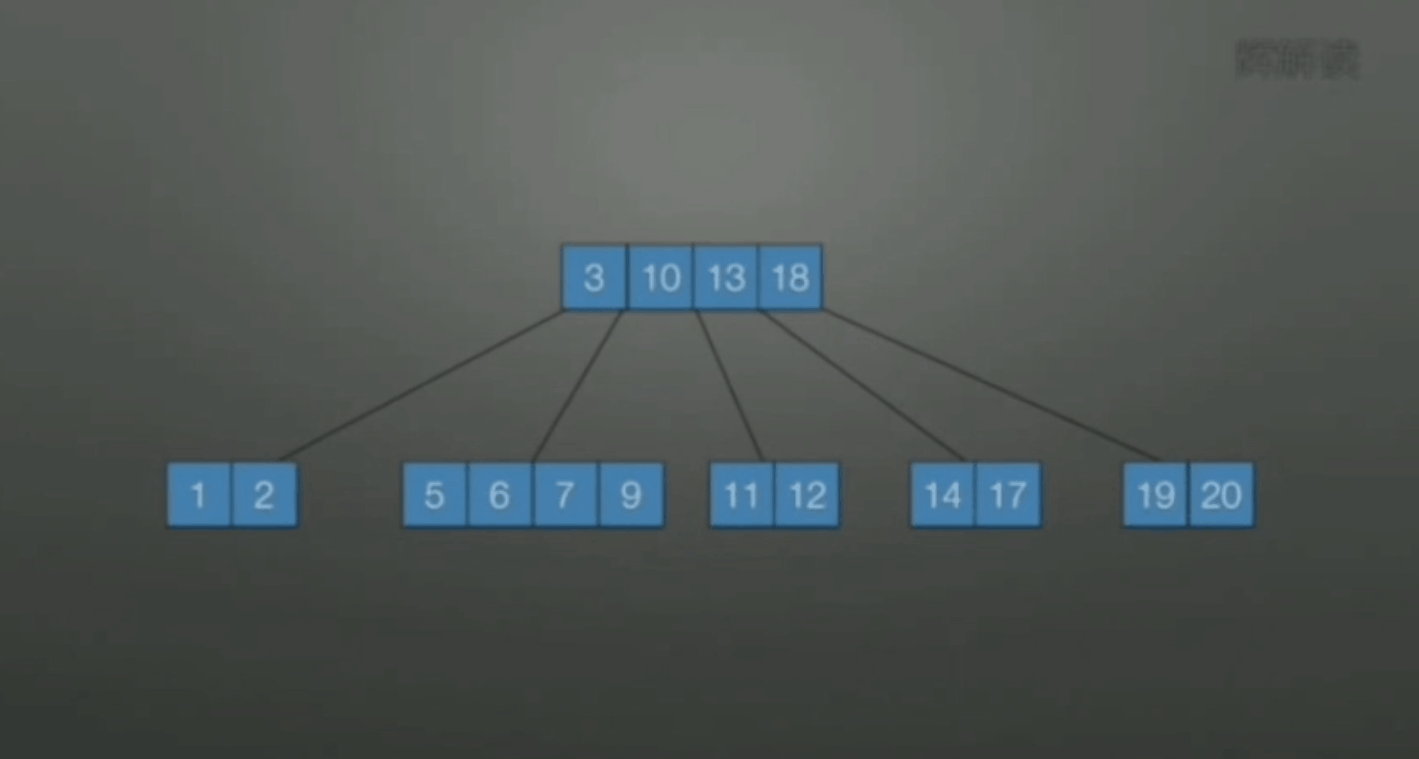
下面是一棵 B-树的例子:

B-树的存储结构

\[\begin{array}{|c|c|c|c|c|c|} \hline \mathrm{n} & \text { Key }_1 & \text { Key }_{2} & \ldots & \text { Key}_{n-1} & \text { Key}_n \\ \hline \mathrm{p}_{0} & \mathrm{p}_{1} & \mathrm{p}_{2} & \ldots & \mathrm{p}_{n-1} & \mathrm{p}_n \\ \hline \end{array} \]

其中, n 为当前结点关键字个数, \(\text{p}_i\) 是指向孩子结点的指针.

性质

对于 m 阶 B-树:

1. 每个结点至多有 m 个分支 (度数最多为 m), 而最少分支数要分情况:
   • 非叶根结点: 最少为 2.
   • 非根且非叶子结点: 最少为 \(\lceil m/2 \rceil\) (即m/2) 向上取整.
2. 有 n 个分支的结点有 n-1 个关键字, 按递增顺序排列.
3. 结点内的各个关键字互不相等.
4. 叶子结点位于同一层, 可以用空指针表示, 是查找失败到达的位置. 入上图中下面的小长方形表示的结点.
5. \(\text{p}_i\) 所指向的结点的所有关键字小于\(\text{Key}_{i+1}\) 大于\(\text{Key}_{i}\) .

注意: 严格来讲, B-树的阶数不是指含有最多关键字结点的度数.

有争议的问题: B-树的高度是否应该包含失败结点? 此处认为是不包括的.

常用操作

查找

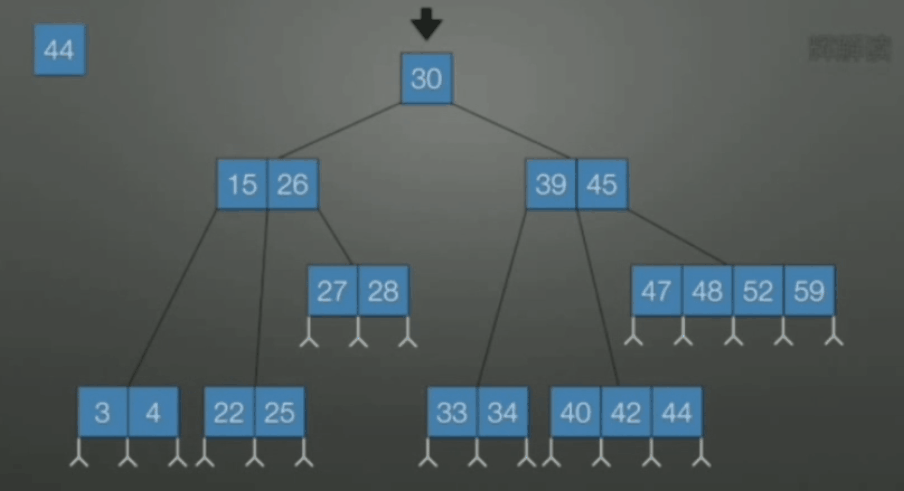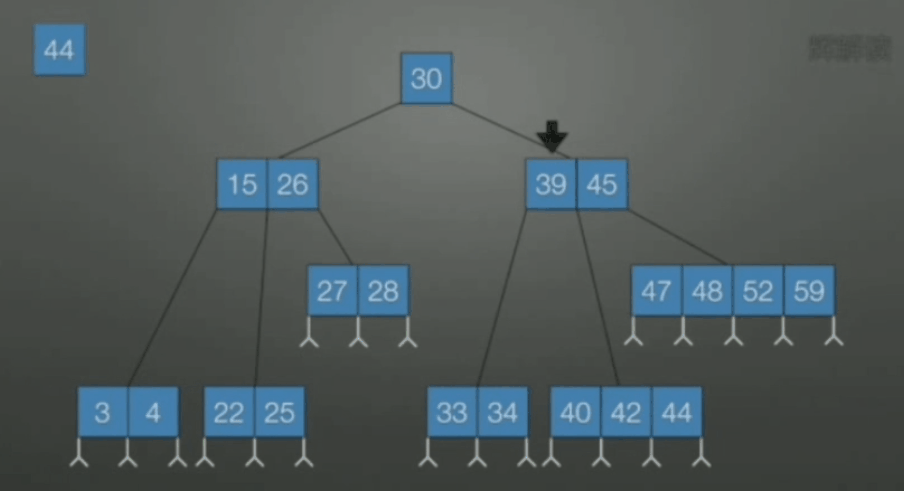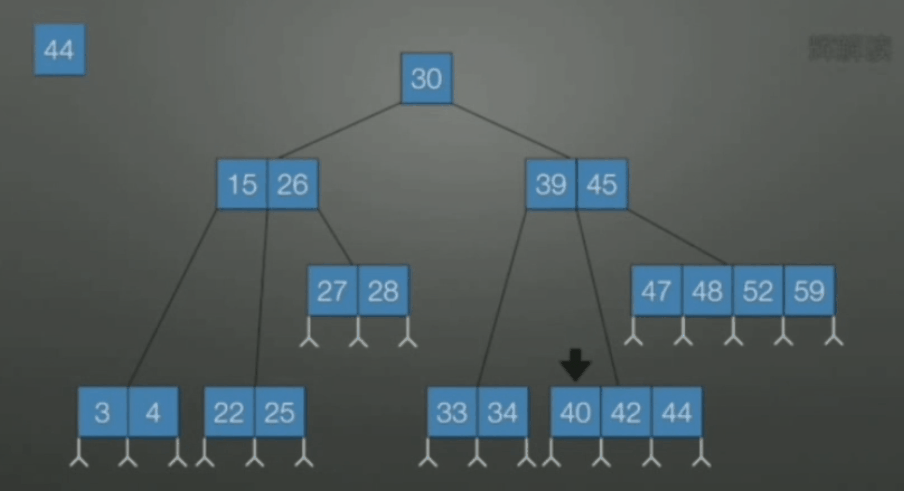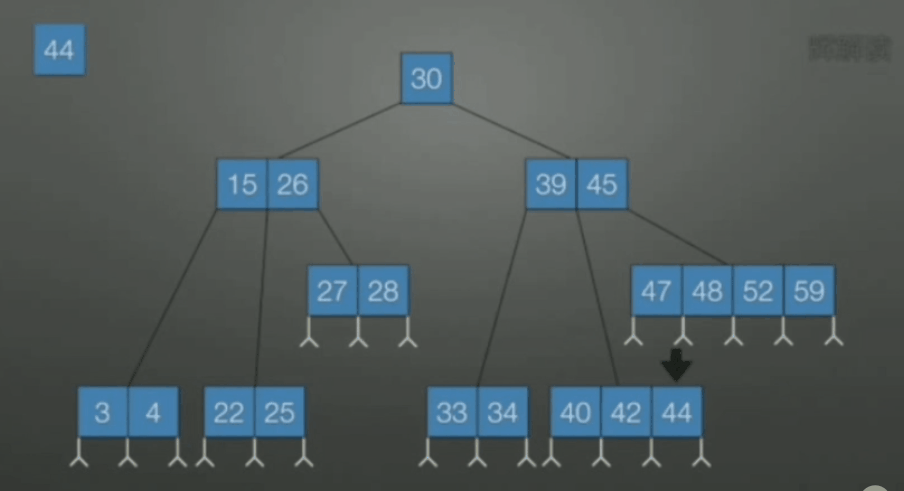
​ 当关键字数不是很多的时候, 可以使用顺序查找, 否则可使用二分查找.

插入

删除

• 直接删除, 位于终端, 且删除后该结点的关键字数仍然大于等于 \(\lceil m/2 \rceil\)

  

• 非终端:用左子树最大关键字或者右子树最小关键字取代.

选择关键字数不小于 \(\lceil m/2 \rceil\) 的子结点进行取代.

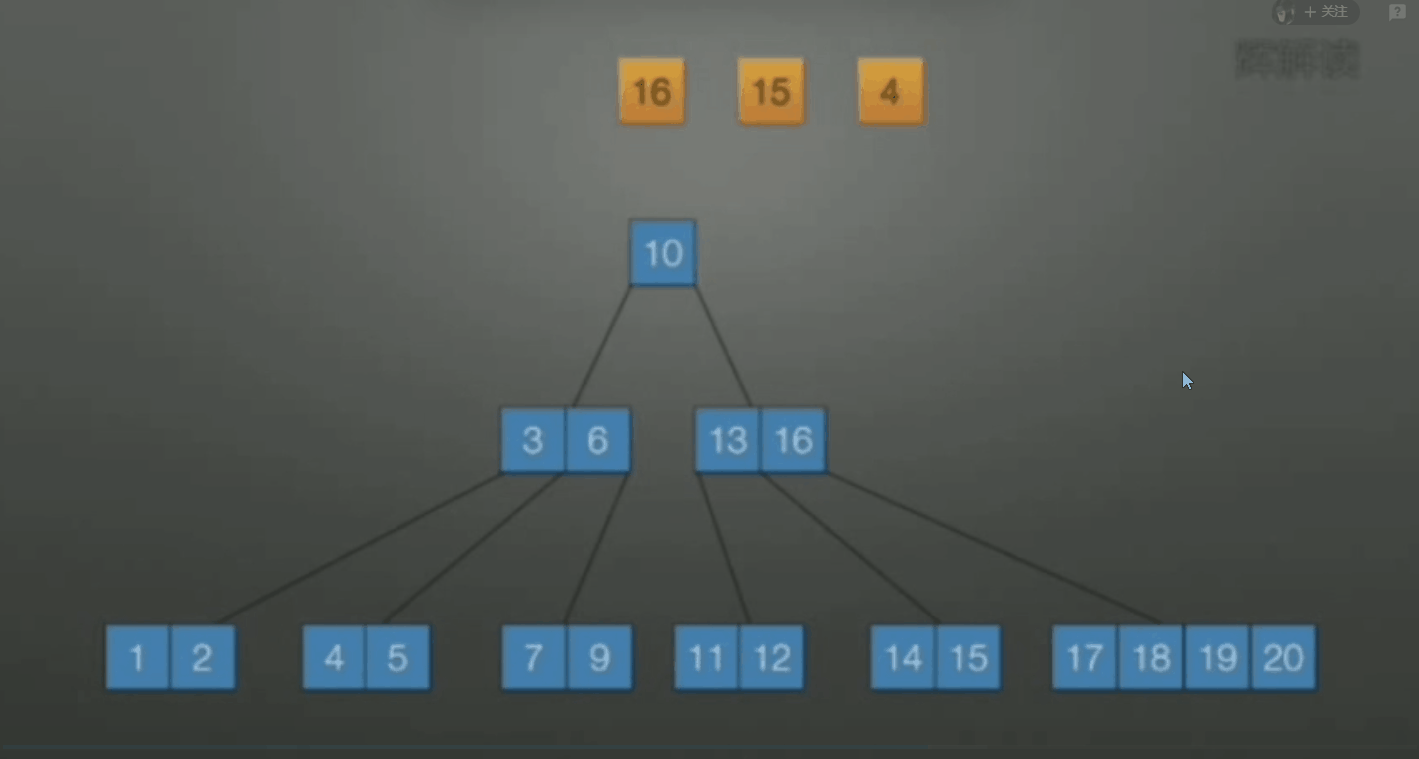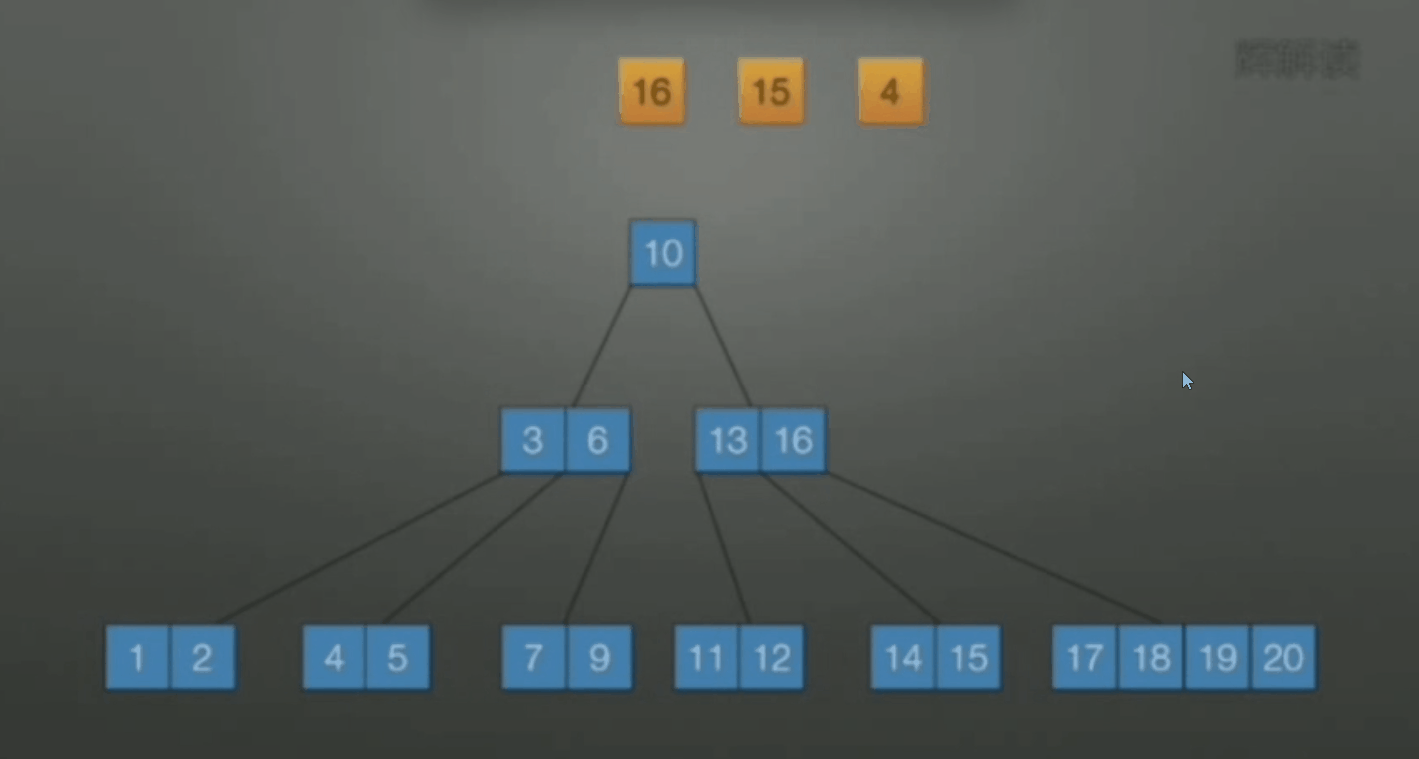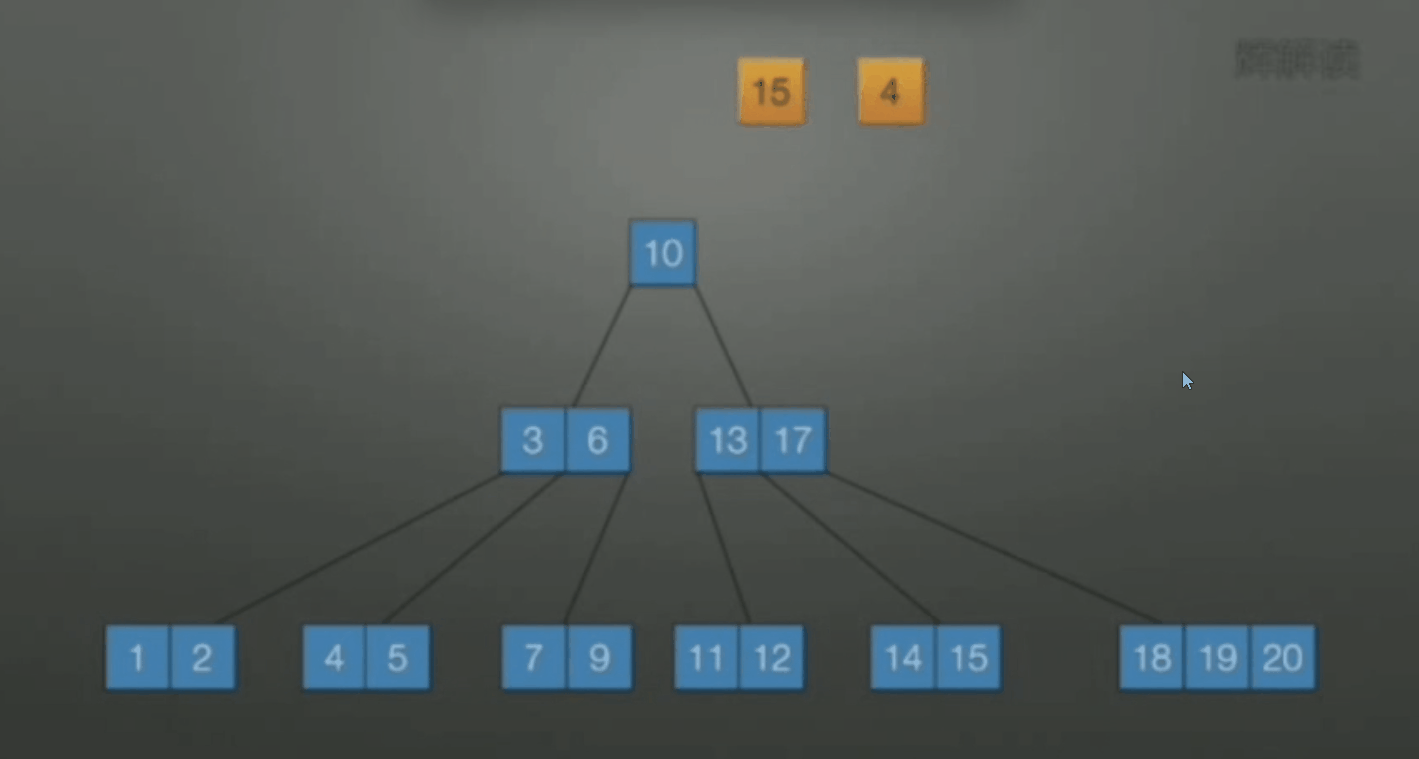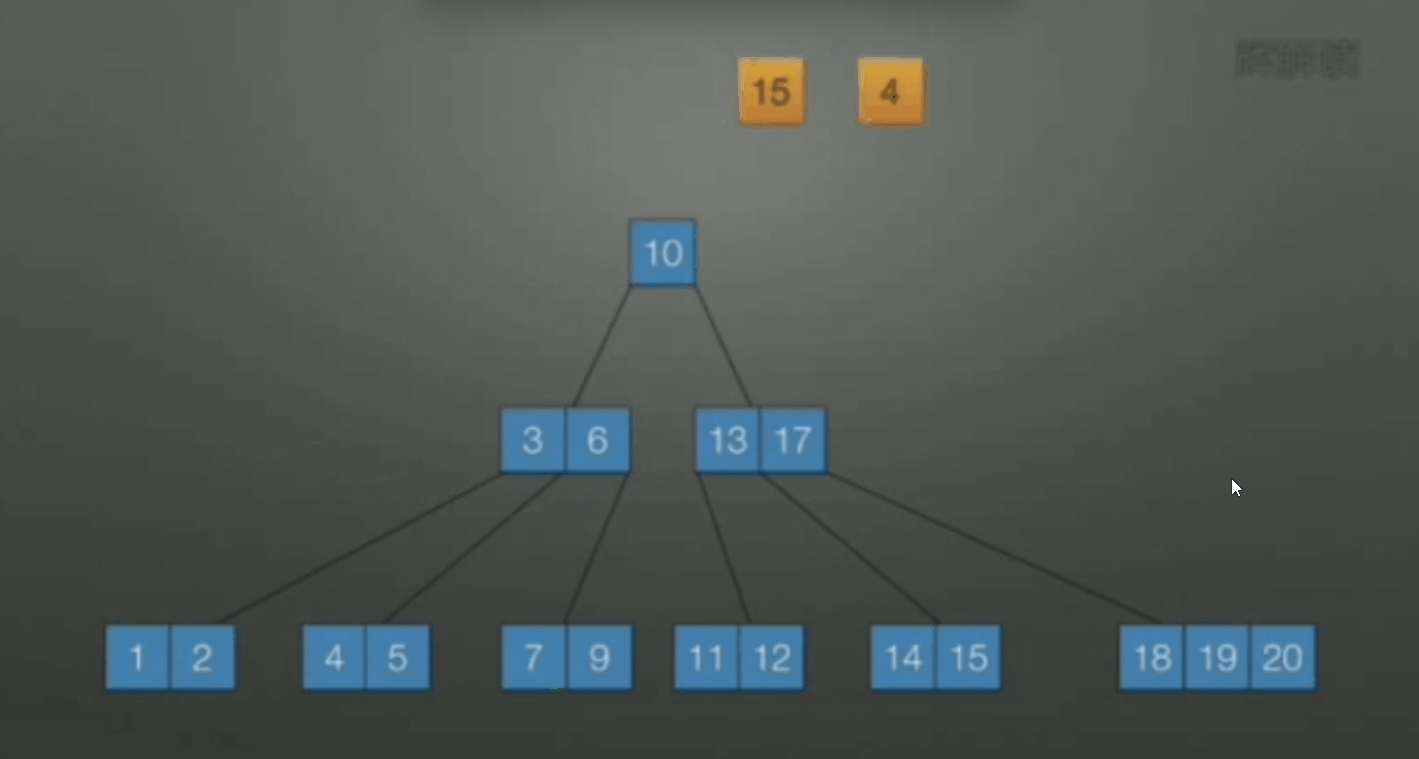
• 当删除后关键字数小于 \(\lceil m/2 \rceil\) , 向兄弟借

  

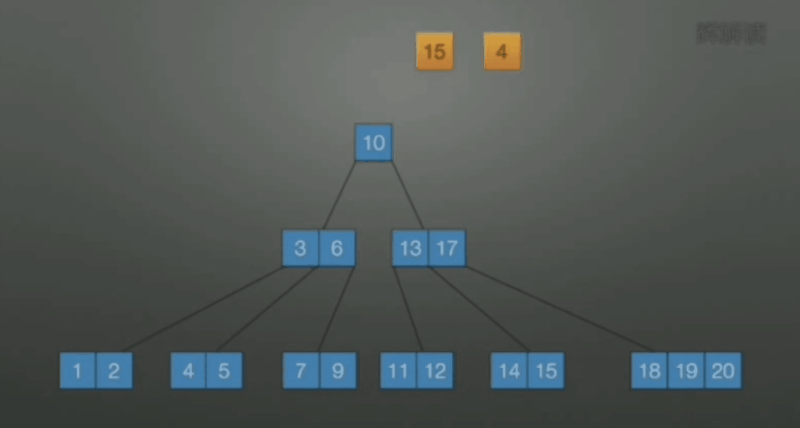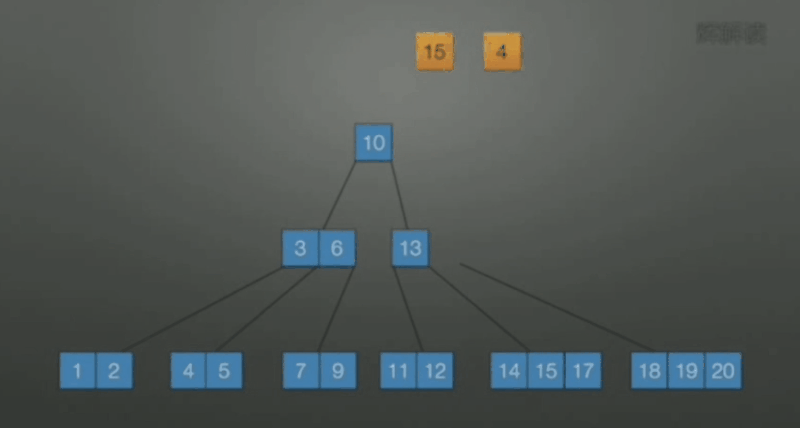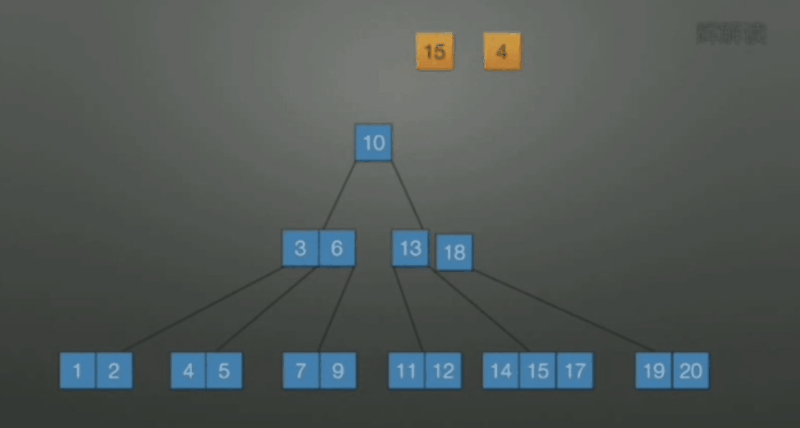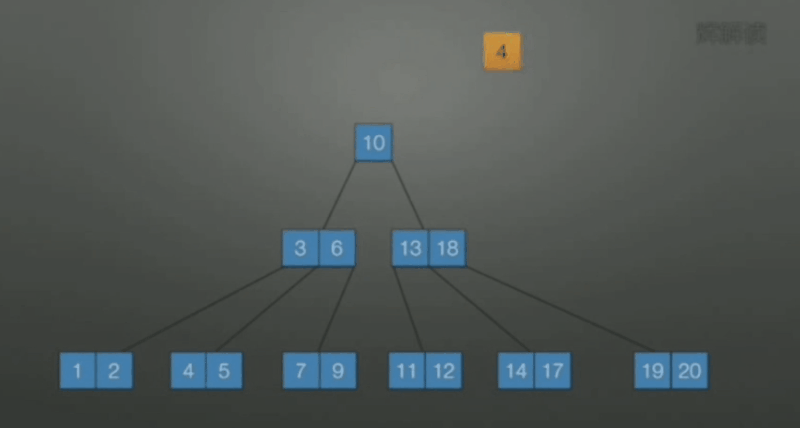
• 若该结点和左右兄弟关键字数都达到下限, 无法再借, 此时合并. 原则上选择较少关键字数目的结点进行合并.

  

标签：结点,text,lceil,关键字,Key,数据结构,mathrm
来源： https://www.cnblogs.com/Jyaoushingan/p/14275297.html