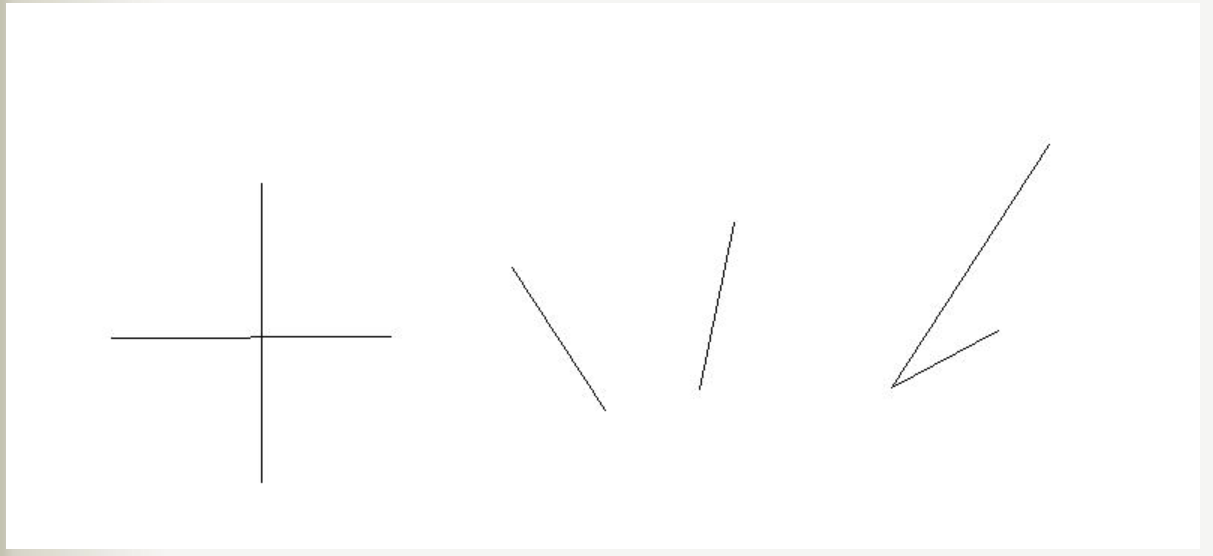kuangbin带你飞 专题十三 基础计算几何
作者:互联网
- POJ 2318 TOYS
- POJ 2398 Toy Storage
- POJ 3304 Segments
- POJ 1269 Intersecting Lines
- POJ 1556 The Doors
- POJ 2653 Pick-up sticks
- POJ 1066 Treasure Hunt
- POJ 1410 Intersection
- POJ 1696 Space Ant
- POJ 3347 Kadj Squares
- POJ 2826 An Easy Problem?!
- POJ 1039 Pipe
- POJ 3349 Geometric Shapes
- POJ 1584 A Round Peg in a Ground Hole
终于写完了...POJ年久失修,导致很多没来由的错误,需要调试很久....
POJ 2318 TOYS
大意:
一个收纳盒,其中有n个隔板,给出每个隔板的左上角和右下角坐标,然后给出m个点的坐标,最后问每个隔板隔出来的小空间有多少个点
思路:
直接判断点和直线的位置关系即可,但是直接\(n^2\)算法会炸,因为有多组测试样例,需要二分去查找,另外cincout也会炸,调了好久....
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 5e4 + 5;
typedef long long LL;
int n, m, cnt[N];
double x1, y1, x2, y2, u[N], l[N];
// 计算几何模板
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
if (fabs(x) < eps) return 0; // =0
if (x < 0)
return -1; // < 0
else
return 1; // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }
struct Point {
double x, y;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
bool operator==(Point b) const {
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const {
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
//叉积
double operator^(const Point &b) const { return x * b.y - y * b.x; }
//点积
double operator*(const Point &b) const { return x * b.x + y * b.y; }
};
struct Line {
Point s, e;
Line() {}
// 两点确定一条线段
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
//返回点和直线(方向向量)关系
// 1 在左侧; 2 在右侧; 3 在直线上
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
};
bool check(int mid,double x,double y){
Point S= Point(u[mid],y1);
Point T = Point(l[mid], y2);
Line L = Line(S, T);
Point now = Point(x, y);
if(L.relation(now)==2){
return true;
}
else
return false;
}
int main(){
int f = 0;
while(scanf("%d",&n)&&(n!=0)){
scanf("%d%lf%lf%lf%lf", &m,& x1, & y1, & x2, & y2);
for (int i = 0; i < n;i++){
scanf("%lf%lf", & u[i], & l[i]);
cnt[i] = 0;
}
cnt[n] = 0;
u[n] = x2;
l[n] = x2;
for (int i = 0; i < m;i++){
double x, y;
scanf("%lf%lf", &x, &y);
int ll = 0, rr = n;
while(ll<rr){
int mid = (ll + rr) >> 1;
if(check(mid,x,y)){
rr = mid;
}
else{
ll = mid + 1;
}
}
cnt[ll]++;
}
if(f)
printf("\n");
for (int i = 0; i <= n;i++){
printf("%d: %d\n", i, cnt[i]);
}
f = 1;
}
return 0;
}
POJ 2398 Toy Storage
大意&思路:
和上一题差不多,但是输入不保证每个隔板都是从左到右输入的,所以需要排序,这里根据每个隔板最左边的点排序即可。输出要求是对于从小到大的t(t>0),输出有t个点的隔板数量,只需要加个map存一下即可.
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 1e3 + 5;
typedef long long LL;
int n, m, cnt[N];
double x1, y1, x2, y2;
// 计算几何模板
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
if (fabs(x) < eps) return 0; // =0
if (x < 0)
return -1; // < 0
else
return 1; // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }
struct Point {
double x, y;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
bool operator==(Point b) const {
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const {
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
//叉积
double operator^(const Point &b) const { return x * b.y - y * b.x; }
//点积
double operator*(const Point &b) const { return x * b.x + y * b.y; }
};
struct Line {
Point s, e;
Line() {}
// 两点确定一条线段
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
//返回点和直线(方向向量)关系
// 1 在左侧; 2 在右侧; 3 在直线上
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
};
struct node{
double u, l;
} a[N];
bool check(int mid,double x,double y){
Point S= Point(a[mid].u,y1);
Point T = Point(a[mid].l, y2);
Line L = Line(S, T);
Point now = Point(x, y);
if(L.relation(now)==2){
return true;
}
else
return false;
}
bool cmp(node a,node b){
return (min(a.l, a.u) < min(b.l, b.u));
}
int main(){
int f = 0;
while(scanf("%d",&n)&&(n!=0)){
scanf("%d%lf%lf%lf%lf", &m,& x1, & y1, & x2, & y2);
for (int i = 0; i < n;i++){
scanf("%lf%lf", & a[i].u, & a[i].l);
cnt[i] = 0;
}
cnt[n] = 0;
a[n].u = x2;
a[n].l = x2;
sort(a, a + n + 1, cmp);
for (int i = 0; i < m;i++){
double x, y;
scanf("%lf%lf", &x, &y);
int ll = 0, rr = n;
while(ll<rr){
int mid = (ll + rr) >> 1;
if(check(mid,x,y)){
rr = mid;
}
else{
ll = mid + 1;
}
}
cnt[ll]++;
}
printf("Box\n");
map<int,int> mp;
for (int i = 0; i <= n;i++){
mp[cnt[i]]++;
}
map<int, int>::iterator it;
for (it = mp.begin(); it != mp.end();it++){
if(it->first!=0)
printf("%d: %d\n", it->first, it->second);
}
}
return 0;
}
POJ 3304 Segments
大意:
给出n个线段,问能否找到一条直线,使得这n个线段在这条直线上的投影至少都有一个点重合
思路:
假设能找到这条直线,那么过重合的点做直线的垂线,这条垂线必然与每个线段都有交点,所以题目转化为了能否找到一个与n个线段都有交点的直线。只需要枚举所有端点,让两个端点确定一条直线判断即可(画个图可以发现,端点可以确定边界条件)。注意需要舍弃过近的点。
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int t, n;
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
if (fabs(x) < eps) return 0; // =0
if (x < 0)
return -1; // < 0
else
return 1; // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }
struct Point {
double x, y;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
bool operator==(Point b) const {
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const {
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
//叉积
double operator^(const Point &b) const { return x * b.y - y * b.x; }
//点积
double operator*(const Point &b) const { return x * b.x + y * b.y; }
//返回向量长度
double len() {
// hypot(x, y), 即sqrt(x * x + y * y)
return hypot(x, y); //库函数
}
Point operator+(const Point &b) const { return Point(x + b.x, y + b.y); }
Point operator*(const double &k) const { return Point(x * k, y * k); }
Point operator/(const double &k) const { return Point(x / k, y / k); }
};
struct Line {
Point s, e;
Line() {}
// 两点确定一条线段
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
// 判断直线是否相等
bool operator==(Line v) { return (s == v.s) && (e == v.e); }
//一个点和倾斜角angle确定直线,0<=angle<pi
Line(Point p, double angle) {
s = p;
if (sgn(angle - pi / 2) == 0) {
e = (s + Point(0, 1));
} else {
e = (s + Point(1, tan(angle)));
}
}
// 保证直线的两个端点满足:s < e
void adjust() {
if (e < s) swap(s, e);
}
//返回直线倾斜角 0<=angle<pi
double angle() {
double k = atan2(e.y - s.y, e.x - s.x);
if (sgn(k) < 0) k += pi;
if (sgn(k - pi) == 0) k -= pi;
return k;
}
//返回点和直线关系
// 1 在左侧; 2 在右侧; 3 在直线上
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
// 点在线段上的判断
bool pointonseg(Point p) {
return sgn((p - s) ^ (e - s)) == 0 && sgn((p - s) * (p - e)) <= 0;
}
// 两向量平行(对应直线平行或重合)
bool parallel(Line v) { return sgn((e - s) ^ (v.e - v.s)) == 0; }
//直线和线段相交判断
//-*this line -v seg
// 2 规范相交
// 1 非规范相交
// 0 不相交
int linecrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
if ((d1 ^ d2) == -2) return 2;
return (d1 == 0 || d2 == 0);
}
};
Line l[105];
Point a[205];
int main(){
cin >> t;
while(t--){
cin>>n;
for (int i = 0; i < n;i++){
Point s, t;
scanf("%lf%lf%lf%lf", &s.x, &s.y, &t.x, &t.y);
l[i] = Line(s, t);
a[2 * i] = s;
a[2 * i + 1] = t;
}
int yes = 0;
for (int i = 0; i < 2 * n&&yes==0;i++){
for (int j = i+1; j < 2 * n&&yes==0;j++){
if(a[i]==a[j])
continue;
Line now = Line(a[i], a[j]);
int flag = 1;
for (int k = 0; k < n;k++){
if (now.linecrossseg(l[k])==0){
flag = 0;
break;
}
}
if(flag){
yes = 1;
}
}
}
if(yes)
cout << "Yes!" << endl;
else
cout << "No!" << endl;
}
return 0;
}
POJ 1269 Intersecting Lines
大意:
n组询问,问两条直线的关系,平行、重合还是相交,相交的话输出交点。
思路:
简单板子题,poj上G++要用%.2f C++用 %.2lf ...WA了好几发
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
if (fabs(x) < eps) return 0; // =0
if (x < 0)
return -1; // < 0
else
return 1; // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }
struct Point {
double x, y;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
bool operator==(Point b) const {
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const {
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
//叉积
double operator^(const Point &b) const { return x * b.y - y * b.x; }
//点积
double operator*(const Point &b) const { return x * b.x + y * b.y; }
//返回向量长度
double len() {
// hypot(x, y), 即sqrt(x * x + y * y)
return hypot(x, y); //库函数
}
Point operator+(const Point &b) const { return Point(x + b.x, y + b.y); }
Point operator*(const double &k) const { return Point(x * k, y * k); }
Point operator/(const double &k) const { return Point(x / k, y / k); }
};
struct Line {
Point s, e;
Line() {}
// 两点确定一条线段
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
// 判断直线是否相等
bool operator==(Line v) { return (s == v.s) && (e == v.e); }
//一个点和倾斜角angle确定直线,0<=angle<pi
Line(Point p, double angle) {
s = p;
if (sgn(angle - pi / 2) == 0) {
e = (s + Point(0, 1));
} else {
e = (s + Point(1, tan(angle)));
}
}
// 保证直线的两个端点满足:s < e
void adjust() {
if (e < s) swap(s, e);
}
//返回直线倾斜角 0<=angle<pi
double angle() {
double k = atan2(e.y - s.y, e.x - s.x);
if (sgn(k) < 0) k += pi;
if (sgn(k - pi) == 0) k -= pi;
return k;
}
//返回点和直线关系
// 1 在左侧; 2 在右侧; 3 在直线上
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
// 点在线段上的判断
bool pointonseg(Point p) {
return sgn((p - s) ^ (e - s)) == 0 && sgn((p - s) * (p - e)) <= 0;
}
// 两向量平行(对应直线平行或重合)
bool parallel(Line v) { return sgn((e - s) ^ (v.e - v.s)) == 0; }
//两直线关系
// 0 平行;1 重合;2 相交
int linecrossline(Line v) {
if ((*this).parallel(v)) return v.relation(s) == 3;
return 2;
}
//求两直线的交点
//要保证两直线不平行或重合
Point crosspoint(Line v) {
double a1 = (v.e - v.s) ^ (s - v.s);
double a2 = (v.e - v.s) ^ (e - v.s);
return Point((s.x * a2 - e.x * a1) / (a2 - a1),
(s.y * a2 - e.y * a1) / (a2 - a1));
}
};
int n;
int main(){
scanf("%d", &n);
printf("INTERSECTING LINES OUTPUT\n");
while(n--){
Point s1, t1, s2, t2;
scanf("%lf%lf%lf%lf%lf%lf%lf%lf", &s1.x, &s1.y, &t1.x, &t1.y, &s2.x, &s2.y, &t2.x, &t2.y);
Line l1 = Line(s1, t1);
Line l2 = Line(s2, t2);
if(l1.linecrossline(l2)==0){
printf("NONE\n");
}
else if(l1.linecrossline(l2)==1){
printf("LINE\n") ;
}
else{
Point P = l1.crosspoint(l2);
printf("POINT %.2lf %.2lf\n", P.x, P.y);
}
}
printf("END OF OUTPUT\n");
return 0;
}
POJ 1556 The Doors
大意:
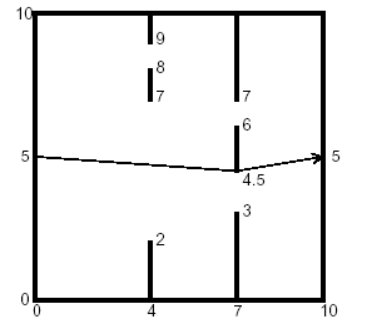
一个房间内有n(\(n<=10\))个隔板,每个隔板上面有两个开口,问从墙壁中央走到右边墙壁中央的最短路是多少
思路:
直接暴力枚举每对端点,然后判断能否直接到达,如果能直接到达则连一条线,最后跑一遍最短路即可
PS:由于poj太过古老,hypot 必须要用G++,而G++输出double需要用.f,用.lf会wa...另外distance也不能用,需要用dist....
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int n;
double dis[100][100];
// 计算几何模板
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
if (fabs(x) < eps) return 0; // =0
if (x < 0)
return -1; // < 0
else
return 1; // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }
struct Point {
double x, y;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
bool operator==(Point b) const {
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const {
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
//叉积
double operator^(const Point &b) const { return x * b.y - y * b.x; }
//点积
double operator*(const Point &b) const { return x * b.x + y * b.y; }
//返回两点的距离
double dist(Point p) { return hypot(x - p.x, y - p.y); }
};
struct Line {
Point s, e;
Line() {}
// 两点确定一条线段
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
//返回点和直线(方向向量)关系
// 1 在左侧; 2 在右侧; 3 在直线上
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
//两线段相交判断:规范相交:交点不在端点
// 2 规范相交;1 非规范相交;0 不相交
int segcrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2) return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
};
Line l[100];
int main(){
int n;
double x, y1, y2, y3, y4;
while(scanf("%d",&n)==1){
if(n==-1)
break;
for (int i = 1; i <= n;i++){
scanf("%lf%lf%lf%lf%lf", &x, &y1, &y2, &y3, &y4);
l[2 * i - 1] = Line(Point(x, y1), Point(x, y2));
l[2 * i] = Line(Point(x, y3), Point(x, y4));
}
for (int i = 0; i <= 4 * n+1;i++){
for (int j = 0; j <= 4 * n+1;j++){
if(i==j)
dis[i][j] = 0;
else
dis[i][j] = inf;
}
}
for (int i = 1; i <= 4 * n;i++){
Line now;
Point temp;
if(i&1) //选择端点
temp = l[(i + 1) / 2].e;
else
temp = l[(i + 1) / 2].s;
now = Line(Point(0, 5), temp);
int col = (i + 3) / 4; //计算当前处于第几列
int flag = 1; //判断起点能否到当前点
for (int j = 1; j < col;j++){
if(now.segcrossseg(l[2*j-1])==0&&now.segcrossseg(l[2*j])==0){
flag = 0;
break;
}
}
if(flag){
dis[0][i] = dis[i][0] = Point(0, 5).dist(temp);
}
flag = 1; //判断当前点能否到终点
now = Line(Point(10, 5), temp);
for (int j = col + 1; j <= n;j++){
if(now.segcrossseg(l[2*j-1])==0&&now.segcrossseg(l[2*j])==0){
flag = 0;
break;
}
}
if(flag){
dis[4 * n + 1][i] = dis[i][4 * n + 1] = Point(10, 5).dist(temp);
}
for (int j = i + 1; j <= 4 * n; j++){ //判断中间的线能不能连
Point temp2;
if(j&1) //选择端点
temp2 = l[(j + 1) / 2].e;
else
temp2 = l[(j + 1) / 2].s;
now = Line(temp, temp2);
int col2 = (j + 3) / 4;
int flag = 1;
for (int k = col+1; k < col2;k++){
if(now.segcrossseg(l[2*k])==0&&now.segcrossseg(l[2*k-1])==0){
flag=0;
break;
}
}
if(flag){
dis[i][j] = dis[j][i] = temp.dist(temp2);
}
}
}
int flag = 1; //判断能否起点到终点直接相连
for (int i = 1; i <= n;i++){
Line now = Line(Point(0, 5), Point(10, 5));
if(now.segcrossseg(l[2*i])==0&&now.segcrossseg(l[2*i-1])==0){
flag = 0;
break;
}
}
if(flag)
dis[0][4 * n + 1] = dis[4 * n + 1][0] = 10;
for (int k = 0; k <= 4 * n + 1;k++)
for (int i = 0; i <= 4 * n + 1;i++)
for (int j = 0; j <= 4 * n + 1;j++)
dis[i][j] = min(dis[i][j], dis[i][k]+dis[k][j]);
printf("%.2f\n", dis[0][4 * n + 1]);
}
return 0;
}
POJ 2653 Pick-up sticks
大意:
按顺序给出n(\(n<=1e5\))个线段,问最后在最上面的(没被其他线段压住)的线段有哪些
思路:
判断线段是否相交即可,本来觉得\(n^2\)算法过不了,也想不出什么\(nlog(n)\)的算法,搜一下题解居然都是\(n^2\)的算法,可能是数据太弱吧.....
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 1e5 + 5;
typedef long long LL;
int n;
// 计算几何模板
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
if (fabs(x) < eps) return 0; // =0
if (x < 0)
return -1; // < 0
else
return 1; // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }
struct Point {
double x, y;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
bool operator==(Point b) const {
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const {
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
//叉积
double operator^(const Point &b) const { return x * b.y - y * b.x; }
//点积
double operator*(const Point &b) const { return x * b.x + y * b.y; }
//返回两点的距离
double dist(Point p) { return hypot(x - p.x, y - p.y); }
};
struct Line {
Point s, e;
Line() {}
// 两点确定一条线段
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
//返回点和直线(方向向量)关系
// 1 在左侧; 2 在右侧; 3 在直线上
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
//两线段相交判断:规范相交:交点不在端点
// 2 规范相交;1 非规范相交;0 不相交
int segcrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2) return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
};
Line l[N];
int istop[N];
int main(){
while(scanf("%d",&n)&&(n!=0)){
for (int i = 0; i < n;i++){
istop[i] = 1;
}
for (int i = 0; i < n; i++)
{
double x1, y1, x2, y2;
scanf("%lf%lf%lf%lf", &x1, &y1, &x2, &y2);
l[i] = Line(Point(x1, y1), Point(x2, y2));
}
for (int i = 0; i < n;i++){
if(istop[i]==0)
continue;
for (int j = i+1; j < n; j++)
{
if(l[i].segcrossseg(l[j])){
istop[i] = 0;
break;
}
}
}
printf("Top sticks: ");
int f = 1;
for (int i = 0; i < n;i++){
if(istop[i]){
if(f)
printf("%d", i + 1), f = 0;
else
printf(", %d", i + 1);
}
}
printf(".\n");
}
return 0;
}
POJ 1066 Treasure Hunt
大意:
一个100x100的房间,n堵墙,再给定宝藏存放的坐标,现在需要从房间外面凿穿墙壁,问最少需要凿多少墙。要求凿墙的位置必须是两个墙根的中点。
思路:
将每个点分别按照四面墙的位置存好,排序,然后模拟判断线段相交即可。
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 1e5 + 5;
typedef long long LL;
int n;
// 计算几何模板
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
if (fabs(x) < eps) return 0; // =0
if (x < 0)
return -1; // < 0
else
return 1; // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }
struct Point {
double x, y;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
bool operator==(Point b) const {
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const {
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
//叉积
double operator^(const Point &b) const { return x * b.y - y * b.x; }
//点积
double operator*(const Point &b) const { return x * b.x + y * b.y; }
//返回两点的距离
double dist(Point p) { return hypot(x - p.x, y - p.y); }
Point operator+(const Point &b) const { return Point(x + b.x, y + b.y); }
Point operator*(const double &k) const { return Point(x * k, y * k); }
Point operator/(const double &k) const { return Point(x / k, y / k); }
};
struct Line {
Point s, e;
Line() {}
// 两点确定一条线段
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
//返回点和直线(方向向量)关系
// 1 在左侧; 2 在右侧; 3 在直线上
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
//两线段相交判断:规范相交:交点不在端点
// 2 规范相交;1 非规范相交;0 不相交
int segcrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2) return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
//直线和线段相交判断
//-*this line -v seg
// 2 规范相交
// 1 非规范相交
// 0 不相交
int linecrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
if ((d1 ^ d2) == -2) return 2;
return (d1 == 0 || d2 == 0);
}
};
Line l[35];
Point lp[100], rp[100], up[100], dp[100];
int ln, rn, un, dn;
int main(){
cin>>n;
for(int i=0;i<n;i++){
double x1, y1, x2, y2;
cin >> x1 >> y1 >> x2 >> y2;
l[i] = Line(Point(x1, y1), Point(x2, y2));
if(x1==0)
lp[ln++] = Point(x1, y1);
if(x1==100)
rp[rn++] = Point(x1, y1);
if(x2==0)
lp[ln++] = Point(x2, y2);
if(x2==100)
rp[rn++] = Point(x2, y2);
if(y1==0)
dp[dn++] = Point(x1, y1);
if(y1==100)
up[un++] = Point(x1, y1);
if(y2==0)
dp[dn++] = Point(x2, y2);
if(y2==100)
up[un++] = Point(x2, y2);
}
lp[ln++] = Point(0.0, 100.0);
lp[ln++] = Point(0.0, 0.0);
rp[rn++] = Point(100.0, 100.0);
rp[rn++] = Point(100.0, 0);
up[un++] = Point(0, 100.0);
up[un++] = Point(100.0, 100.0);
dp[dn++] = Point(0.0, 0.0);
dp[dn++] = Point(100, 0.0);
double sx, sy;
cin >> sx >> sy;
Point S = Point(sx, sy);
sort(lp, lp + ln);
sort(rp, rp + rn);
sort(dp, dp + dn);
sort(up, up + un);
int res = 0x3f3f3f3f;
for (int i = 0; i < ln - 1;i++){
if(lp[i]==lp[i+1])
continue;
Line now = Line((lp[i] + lp[i + 1]) / 2, S);
int cnt = 0;
for (int j = 0; j < n;j++){
if(now.segcrossseg(l[j])==2)
cnt++;
}
res = min(res, cnt);
}
for (int i = 0; i < rn - 1;i++){
if(rp[i]==rp[i+1])
continue;
Line now = Line((rp[i] + rp[i + 1]) / 2, S);
int cnt = 0;
for (int j = 0; j < n;j++){
if(now.segcrossseg(l[j])==2)
cnt++;
}
res = min(res, cnt);
}
for (int i = 0; i < dn - 1;i++){
if(dp[i]==dp[i+1])
continue;
Line now = Line((dp[i] + dp[i + 1]) / 2, S);
int cnt = 0;
for (int j = 0; j < n;j++){
if(now.segcrossseg(l[j])==2)
cnt++;
}
res = min(res, cnt);
}
for (int i = 0; i < un - 1;i++){
if(up[i]==up[i+1])
continue;
Line now = Line((up[i] + up[i + 1]) / 2, S);
int cnt = 0;
for (int j = 0; j < n;j++){
if(now.segcrossseg(l[j])==2)
cnt++;
}
res = min(res, cnt);
}
cout << "Number of doors = " << res + 1 << endl;
}
POJ 1410 Intersection
大意:
给出一个实心的矩形,以及一个线段,问二者是否有交点
思路:
一开始只用了矩形四条边是否与线段相交来判断,后来发现矩形是实心的,所以要判断线段的两个端点是否在矩形范围内,一开始写的叉积但是wa了,后来想想只需要按照坐标关系判断即可。另外需要注意的是输入并不一定是先输入矩形的左上角再输入右下角,所以需要判断一下。
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 1e5 + 5;
typedef long long LL;
int n;
// 计算几何模板
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
if (fabs(x) < eps) return 0; // =0
if (x < 0)
return -1; // < 0
else
return 1; // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }
struct Point {
double x, y;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
bool operator==(Point b) const {
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const {
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
//叉积
double operator^(const Point &b) const { return x * b.y - y * b.x; }
//点积
double operator*(const Point &b) const { return x * b.x + y * b.y; }
//返回两点的距离
double dist(Point p) { return hypot(x - p.x, y - p.y); }
Point operator+(const Point &b) const { return Point(x + b.x, y + b.y); }
Point operator*(const double &k) const { return Point(x * k, y * k); }
Point operator/(const double &k) const { return Point(x / k, y / k); }
};
struct Line {
Point s, e;
Line() {}
// 两点确定一条线段
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
//返回点和直线(方向向量)关系
// 1 在左侧; 2 在右侧; 3 在直线上
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
//两线段相交判断:规范相交:交点不在端点
// 2 规范相交;1 非规范相交;0 不相交
int segcrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2) return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
};
int main(){
cin>>n;
while(n--){
double sx, sy, tx, ty, x1, y1, x2, y2;
cin >> sx >> sy >> tx >> ty >> x1 >> y1 >> x2 >> y2;
Line l = Line(Point(sx, sy), Point(tx, ty));
Line up = Line(Point(x1, y1), Point(x2, y1));
Line down = Line(Point(x1, y2), Point(x2, y2));
Line left = Line(Point(x1, y1), Point(x1, y2));
Line right = Line(Point(x2, y1), Point(x2, y2));
if(l.segcrossseg(up)||l.segcrossseg(down)||l.segcrossseg(left)||l.segcrossseg(right))
cout << "T" << endl;
else if(min(x1,x2)<min(sx,tx)&&max(x1,x2)>max(sx,tx)&&min(y1,y2)<min(sy,ty)&&max(y1,y2)>max(sy,ty))
cout << "T" << endl;
else
cout << "F" << endl;
}
}
POJ 1696 Space Ant
大意:
一个蚂蚁只能向前向左走,给出n个点,问最多能走到哪些点,顺序是什么
思路:
从左下角开始一圈一圈的往里走即可,n个点都可以走到,每次走到一个点后,都对后面的点进行一次极角排序即可。
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int t, n;
double dis[100][100];
// 计算几何模板
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
if (fabs(x) < eps) return 0; // =0
if (x < 0)
return -1; // < 0
else
return 1; // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }
struct Point {
double x, y;
int index;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
bool operator==(Point b) const {
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const {
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
//叉积
double operator^(const Point &b) const { return x * b.y - y * b.x; }
//点积
double operator*(const Point &b) const { return x * b.x + y * b.y; }
//返回两点的距离
double dist(Point p) { return hypot(x - p.x, y - p.y); }
};
struct Line {
Point s, e;
Line() {}
// 两点确定一条线段
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
//返回点和直线(方向向量)关系
// 1 在左侧; 2 在右侧; 3 在直线上
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
//两线段相交判断:规范相交:交点不在端点
// 2 规范相交;1 非规范相交;0 不相交
int segcrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2) return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
};
struct cmp {
Point p;
cmp(const Point &p0) { p = p0; }
bool operator()(const Point &aa, const Point &bb) {
Point a = aa, b = bb;
int d = sgn((a - p) ^ (b - p));
if (d == 0) {
return sgn(a.dist(p) - b.dist(p)) < 0;
}
return d > 0;
}
};
// 进行极角排序
// 首先需要找到最左下角的点
// 需要重载号好Point的 < 操作符(min函数要用)
Point p[100];
void norm() {
for (int i = 1; i < n; i++){
if(p[i].y<p[0].y||(p[i].y==p[0].y&&p[i].x<p[0].x))
swap(p[0], p[i]);
}
for (int i = 1; i < n;i++)
sort(p+i, p + n, cmp(p[i-1])); //确定一个点后以这个点为标准进行极角排序
}
int main(){
cin>>t;
while(t--){
cin>>n;
for (int i = 0; i < n;i++){
cin >> p[i].index >> p[i].x >> p[i].y;
}
norm();
cout << n;
for (int i = 0; i < n;i++){
cout << " " << p[i].index;
}
cout << endl;
}
}
POJ 3347 Kadj Squares
大意:
给出n个正方形,要求旋转45度之后按顺序靠右紧贴摆放,问从上面看能看到哪些方块
思路:
首先计算正方形摆放的正确位置,这个遍历一遍前面已经有的正方形即可(具体公式看代码),然后对于每个正方形,判断左边和右边的所有正方形有没有挡住它,如果挡住就更新,最后判断能否输出(所以这个题和计算几何没啥关系...)
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int n;
struct node{
int len, l, r;
} a[55];
int main(){
while(cin>>n){
if(n==0)
break;
for (int i = 0; i < n;i++){
a[i].len = a[i].l = a[i].r = 0;
cin >> a[i].len;
for (int j = 0; j < i;j++){
a[i].l = max(a[i].l, a[j].r - abs(a[j].len - a[i].len));
}
a[i].r = a[i].l + 2 * a[i].len;
}
for (int i = 0; i < n;i++){
for (int j = 0; j < i;j++)
if(a[i].l < a[j].r && a[i].len < a[j].len)
a[i].l = a[j].r;
for(int j = i+1;j < n;j++)
if(a[i].r > a[j].l && a[i].len < a[j].len)
a[i].r = a[j].l;
}
for (int i = 0; i < n;i++){
if(a[i].r>a[i].l)
cout << i + 1 << ' ';
}
cout << endl;
}
return 0;
}
POJ 2826 An Easy Problem?!
大意:
给出两个线段,组成一个容器,问最多能盛多少水
思路:
算三角形面积即可,但是需要注意的是有三种情况直接输出0:
图片来自kuangbin大佬的博客:https://www.cnblogs.com/kuangbin/p/3192511.html
尤其是第三种,比较难以想到,就是上面的线直接挡住了下面的线段,这个可以过下面线段的较高端点向上做垂线看能否与上面的线段相交来判断。
最后输出的时候需要加上eps,否则有可能输出-0导致WA...
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 1e6 + 5;
typedef long long LL;
int t, n;
double dis[100][100];
// 计算几何模板
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
if (fabs(x) < eps) return 0; // =0
if (x < 0)
return -1; // < 0
else
return 1; // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }
struct Point {
double x, y;
int index;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
bool operator==(Point b) const {
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const {
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
//叉积
double operator^(const Point &b) const { return x * b.y - y * b.x; }
//点积
double operator*(const Point &b) const { return x * b.x + y * b.y; }
//返回两点的距离
double dist(Point p) { return hypot(x - p.x, y - p.y); }
// 极角排序
};
struct Line {
Point s, e;
Line() {}
// 两点确定一条线段
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
//返回点和直线(方向向量)关系
// 1 在左侧; 2 在右侧; 3 在直线上
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
//两线段相交判断:规范相交:交点不在端点
// 2 规范相交;1 非规范相交;0 不相交
int segcrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2) return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
bool parallel(Line v) { return sgn((e - s) ^ (v.e - v.s)) == 0; }
//求两直线的交点
//要保证两直线不平行或重合
Point crosspoint(Line v) {
double a1 = (v.e - v.s) ^ (s - v.s);
double a2 = (v.e - v.s) ^ (e - v.s);
return Point((s.x * a2 - e.x * a1) / (a2 - a1),
(s.y * a2 - e.y * a1) / (a2 - a1));
}
double length() { return s.dist(e); }
//点到直线的距离
double dispointtoline(Point p) {
return fabs((p - s) ^ (e - s)) / length();
}
//点到线段的距离
double dispointtoseg(Point p) {
if (sgn((p - s) * (e - s)) < 0 || sgn((p - e) * (s - e)) < 0)
return min(p.dist(s), p.dist(e));
return dispointtoline(p);
}
};
int main(){
cin>>n;
while(n--){
double x1, y1, x2, y2;
cin>>x1>>y1>>x2>>y2;
Line l1 = Line(Point(x1, y1), Point(x2, y2));
cin>>x1>>y1>>x2>>y2;
Line l2 = Line(Point(x1, y1), Point(x2, y2));
if(l1.s.y==l1.e.y||l2.s.y==l2.e.y){
printf("0.00\n");//一条线与x轴平行
continue;
}
else if(l1.segcrossseg(l2)==0){
printf("0.00\n");//不相交
continue;
}
if(l1.s.y<l1.e.y)
swap(l1.e, l1.s);
if(l2.s.y<l2.e.y)
swap(l2.e, l2.s);
if(Line(Point(l1.s.x,100000.0),l1.s).segcrossseg(l2)){
printf("0.00\n");//l2挡住了l1
continue;
}
if(Line(Point(l2.s.x,100000.0),l2.s).segcrossseg(l1)){
printf("0.00\n");//l1挡住了l2
continue;
}
Point top,top2; //三角形的上两个顶点
if(l1.s.y<l2.s.y){
top = l1.s;
top2 = Line(top, Point(100000.0, top.y)).crosspoint(l2);
}
else{
top = l2.s;
top2 = Line(top, Point(100000.0, top.y)).crosspoint(l1);
}
Point p = l1.crosspoint(l2); //三角形的下端点,也是两个线段交点
double res = top.dist(top2) * Line(top, top2).dispointtoline(p) / 2;
printf("%.2f\n", res+eps);
}
return 0;
}
POJ 1039 Pipe
大意:
给出从左到右的n个点,将他们连起线来是管道的上壁,然后每个点对应的y-1的点连起线来作为管道的下壁,现在从管道最左边射入光线,最多能到达多远,输出横坐标,如果能穿过整个管道,输出“Through all the pipe.”
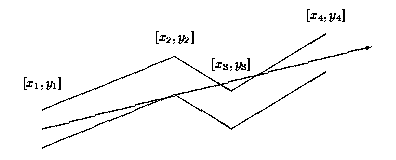
思路:
射的最远的光线,必然是经过一个上拐点和一个下拐点的,否则我们可以通过旋转使得它射的更远,那么可以枚举每个上拐点和下拐点的组合,判断不能经过哪个管道面,假如第k个管道面不能通过,且k>max(i,j),那么就更新答案,否则不需要更新(因为不成立),至于怎么更新答案呢,它必然和管道相交于k-1点和k点之间的上壁或者下壁,判断一下有无交点即可。
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
using namespace std;
const int N = 20 + 5;
typedef long long LL;
int t, n;
double dis[100][100];
// 计算几何模板
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
if (fabs(x) < eps) return 0; // =0
if (x < 0)
return -1; // < 0
else
return 1; // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }
struct Point {
double x, y;
int index;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
bool operator==(Point b) const {
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const {
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
//叉积
double operator^(const Point &b) const { return x * b.y - y * b.x; }
//点积
double operator*(const Point &b) const { return x * b.x + y * b.y; }
//返回两点的距离
double dist(Point p) { return hypot(x - p.x, y - p.y); }
// 极角排序
};
struct Line {
Point s, e;
Line() {}
// 两点确定一条线段
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
//返回点和直线(方向向量)关系
// 1 在左侧; 2 在右侧; 3 在直线上
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
//两线段相交判断:规范相交:交点不在端点
// 2 规范相交;1 非规范相交;0 不相交
int segcrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2) return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
bool parallel(Line v) { return sgn((e - s) ^ (v.e - v.s)) == 0; }
//求两直线的交点
//要保证两直线不平行或重合
Point crosspoint(Line v) {
double a1 = (v.e - v.s) ^ (s - v.s);
double a2 = (v.e - v.s) ^ (e - v.s);
return Point((s.x * a2 - e.x * a1) / (a2 - a1),
(s.y * a2 - e.y * a1) / (a2 - a1));
}
double length() { return s.dist(e); }
//点到直线的距离
double dispointtoline(Point p) {
return fabs((p - s) ^ (e - s)) / length();
}
//点到线段的距离
double dispointtoseg(Point p) {
if (sgn((p - s) * (e - s)) < 0 || sgn((p - e) * (s - e)) < 0)
return min(p.dist(s), p.dist(e));
return dispointtoline(p);
}
//直线和线段相交判断
//-*this line -v seg
// 2 规范相交
// 1 非规范相交
// 0 不相交
int linecrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
if ((d1 ^ d2) == -2) return 2;
return (d1 == 0 || d2 == 0);
}
};
Point upp[N], downp[N];
int main(){
while(scanf("%d",&n)&&n!=0){
for (int i = 0; i < n;i++){
double x, y;
scanf("%lf%lf", &x, &y);
upp[i] = Point(x, y);
downp[i] = Point(x, y - 1.0);
}
int can = 0;
double res = upp[0].x;
for (int i = 0; i < n && can == 0; i++){
for (int j = 0; j < n && can == 0; j++){
if(i==j)
continue;
Line now = Line(upp[i], downp[j]);
int flag = 1;
for (int k = 0; k < n;k++){
Line col = Line(upp[k], downp[k]);
if(now.linecrossseg(col)==0){
flag = 0;
if(k>max(i,j)){
if(now.linecrossseg(Line(downp[k-1],downp[k])))
res = max(res, now.crosspoint(Line(downp[k - 1], downp[k])).x);
if(now.linecrossseg(Line(upp[k-1],upp[k])))
res = max(res, now.crosspoint(Line(upp[k - 1], upp[k])).x);
}
break;
}
}
if(flag){
can = 1;
}
}
}
if(can)
printf("Through all the pipe.\n");
else
printf("%.2f\n", res);
}
}
POJ 3349 Geometric Shapes
大意:
给出多种多边形,问每个多边形和哪些其他的图形相交
思路:
枚举判断即可,输入输出比较恶心......另外还学习了一下输入正方形不是平行于x轴的情况,应该怎么处理输入:
double x1, y1, x2, y2;
scanf(" (%lf,%lf) (%lf,%lf)", &x1, &y1, &x2, &y2);
double x3 = ((x1 + x2) + (y2 - y1)) / 2, y3 = ((y1 + y2) + (x1 - x2)) / 2;
double x4 = ((x1 + x2) - (y2 - y1)) / 2, y4 = ((y1 + y2) - (x1 - x2)) / 2;
mp[name].push_back(Line(Point(x1, y1), Point(x3, y3)));
mp[name].push_back(Line(Point(x1, y1), Point(x4, y4)));
mp[name].push_back(Line(Point(x2, y2), Point(x3, y3)));
mp[name].push_back(Line(Point(x2, y2), Point(x4, y4)));
直接上代码吧:
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
#include <set>
using namespace std;
const int N = 20 + 5;
typedef long long LL;
int t, n;
double dis[100][100];
// 计算几何模板
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
if (fabs(x) < eps) return 0; // =0
if (x < 0)
return -1; // < 0
else
return 1; // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }
struct Point {
double x, y;
int index;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
bool operator==(Point b) const {
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const {
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
Point operator+(const Point &b) const { return Point(x + b.x, y + b.y); }
//叉积
double operator^(const Point &b) const { return x * b.y - y * b.x; }
//点积
double operator*(const Point &b) const { return x * b.x + y * b.y; }
//返回两点的距离
double dist(Point p) { return hypot(x - p.x, y - p.y); }
// 极角排序
};
struct Line {
Point s, e;
Line() {}
// 两点确定一条线段
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
//返回点和直线(方向向量)关系
// 1 在左侧; 2 在右侧; 3 在直线上
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
//两线段相交判断:规范相交:交点不在端点
// 2 规范相交;1 非规范相交;0 不相交
int segcrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2) return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
bool parallel(Line v) { return sgn((e - s) ^ (v.e - v.s)) == 0; }
//求两直线的交点
//要保证两直线不平行或重合
Point crosspoint(Line v) {
double a1 = (v.e - v.s) ^ (s - v.s);
double a2 = (v.e - v.s) ^ (e - v.s);
return Point((s.x * a2 - e.x * a1) / (a2 - a1),
(s.y * a2 - e.y * a1) / (a2 - a1));
}
double length() { return s.dist(e); }
//点到直线的距离
double dispointtoline(Point p) {
return fabs((p - s) ^ (e - s)) / length();
}
//点到线段的距离
double dispointtoseg(Point p) {
if (sgn((p - s) * (e - s)) < 0 || sgn((p - e) * (s - e)) < 0)
return min(p.dist(s), p.dist(e));
return dispointtoline(p);
}
//直线和线段相交判断
//-*this line -v seg
// 2 规范相交
// 1 非规范相交
// 0 不相交
int linecrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
if ((d1 ^ d2) == -2) return 2;
return (d1 == 0 || d2 == 0);
}
};
char name,Type[20];
map<char, vector<Line> > mp;
void inputs(char Type[]){
if(strcmp(Type,"square")==0){
double x1, y1, x2, y2;
scanf(" (%lf,%lf) (%lf,%lf)", &x1, &y1, &x2, &y2);
double x3 = ((x1 + x2) + (y2 - y1)) / 2, y3 = ((y1 + y2) + (x1 - x2)) / 2;
double x4 = ((x1 + x2) - (y2 - y1)) / 2, y4 = ((y1 + y2) - (x1 - x2)) / 2;
mp[name].push_back(Line(Point(x1, y1), Point(x3, y3)));
mp[name].push_back(Line(Point(x1, y1), Point(x4, y4)));
mp[name].push_back(Line(Point(x2, y2), Point(x3, y3)));
mp[name].push_back(Line(Point(x2, y2), Point(x4, y4)));
//cout << "name:" << name << ' ' << "type:" << Type << ' ' << x1 << ' ' << y1 << ' ' << x2 << ' ' << y2 << endl;
}
else if(strcmp(Type,"rectangle")==0){
double x1, y1, x2, y2,x3,y3;
scanf(" (%lf,%lf) (%lf,%lf) (%lf,%lf)", &x1, &y1, &x2, &y2,&x3,&y3);
mp[name].push_back(Line(Point(x1, y1), Point(x2, y2)));
mp[name].push_back(Line(Point(x2, y2), Point(x3, y3)));
Point p4 = (Point(x1, y1) - Point(x2, y2)) + (Point(x3, y3) - Point(x2, y2)) + Point(x2, y2);
mp[name].push_back(Line(Point(x3, y3), p4));
mp[name].push_back(Line(p4, Point(x1, y1)));
//cout << "name:" << name << ' ' << "type:" << Type << ' ' << x1 << ' ' << y1 << ' ' << x2 << ' ' << y2 << endl;
}
else if(strcmp(Type,"line")==0){
double x1, y1, x2, y2;
scanf(" (%lf,%lf) (%lf,%lf)", &x1, &y1, &x2, &y2);
mp[name].push_back(Line(Point(x1, y1), Point(x2, y2)));
}
else if(strcmp(Type,"triangle")==0){
double x1, y1, x2, y2,x3,y3;
scanf(" (%lf,%lf) (%lf,%lf) (%lf,%lf)", &x1, &y1, &x2, &y2,&x3,&y3);
mp[name].push_back(Line(Point(x1, y1), Point(x2, y2)));
mp[name].push_back(Line(Point(x2, y2), Point(x3, y3)));
mp[name].push_back(Line(Point(x3, y3), Point(x1, y1)));
}
else{
int n;
scanf("%d",&n);
double x0,y0,x1, y1, x2, y2;
scanf(" (%lf,%lf)", &x1, &y1);
//cout << x1 << ' ' << y1 << endl;
x0 = x1, y0 = y1;
for (int i = 1; i < n;i++){
scanf(" (%lf,%lf)", &x2, &y2);
//cout << x2 << ' ' << y2 << endl;
mp[name].push_back(Line(Point(x1, y1), Point(x2, y2)));
x1 = x2, y1 = y2;
}
mp[name].push_back(Line(Point(x0, y0), Point(x2, y2)));
}
getchar();
}
map<char, vector<char> > res;
int f = 0;
int main(){
while(scanf("%c",&name)&&name!='.'){
/*
if(name=='-'){
getchar();
printf("\n");
continue;
}*/
mp.clear();
res.clear();
scanf("%s", Type);
inputs(Type);
while(scanf("%c",&name)&&name!='-'){
scanf("%s", Type);
inputs(Type);
}
getchar();
map<char, vector<Line> >::iterator i;
map<char, vector<Line> >::iterator j;
for (i = mp.begin(); i != mp.end();i++){
for (j = mp.begin(); j != mp.end();j++){
if(i==j)
continue;
int have = 0;
for (int p = 0; p < i->second.size();p++){
for (int q = 0; q < j->second.size();q++){
if(i->second[p].segcrossseg(j->second[q])){
have = 1;
}
}
}
if(have)
res[i->first].push_back(j->first);
}
if(res[i->first].size()==0)
printf("%c has no intersections\n", i->first);
else{
if(res[i->first].size()==1)
printf("%c intersects with %c\n", i->first, res[i->first][0]);
else if(res[i->first].size()==2){
printf("%c intersects with %c and %c\n", i->first, res[i->first][0],res[i->first][1]);
}
else{
printf("%c intersects with ", i->first);
for (int it = 0;it<res[i->first].size()-1;it++)
printf("%c, ", res[i->first][it]);
printf("and %c\n", res[i->first][res[i->first].size()-1]);
}
}
}
printf("\n");
}
}
POJ 1584 A Round Peg in a Ground Hole
大意:
给出一个圆和一个多边形,判断多边形是否是凸包,如果是凸包,判断圆是否在凸包内
思路:
判断凸包:相邻两条边的叉积始终同号
判断点在凸包内:逐条枚举n边形的边AB,利用计算PA和PB的夹角,最后求和得到的就是环顾角。
(1)圆心在多边形内部时,环顾角=±360
(2)圆心在多边形外部时,环顾角=0
(3)圆心在多边形边上时(不包括顶点),环顾角=±180
(4)圆心在多边形顶点时,环顾角为(0,360)之间的任意角,其实就是圆心所在的顶点的两条邻接边的夹角
判断圆在凸包内:圆心到每个边的距离大于等于半径
#include <iostream>
#include <string.h>
#include <stdio.h>
#include <vector>
#include <map>
#include <queue>
#include <algorithm>
#include <math.h>
#include <cstdio>
#include <set>
using namespace std;
const int N = 20 + 5;
typedef long long LL;
int t, n;
double dis[100][100];
// 计算几何模板
const double eps = 1e-8;
const double inf = 1e20;
const double pi = acos(-1.0);
const int maxp = 1010;
// 和0做比较
int sgn(double x) {
if (fabs(x) < eps) return 0; // =0
if (x < 0)
return -1; // < 0
else
return 1; // > 0
}
// 计算x的平方
inline double sqr(double x) { return x * x; }
struct Point {
double x, y;
int index;
Point() {}
Point(double _x, double _y) {
x = _x;
y = _y;
}
bool operator==(Point b) const {
return sgn(x - b.x) == 0 && sgn(y - b.y) == 0;
}
bool operator<(Point b) const {
return sgn(x - b.x) == 0 ? sgn(y - b.y) < 0 : x < b.x;
}
Point operator-(const Point &b) const { return Point(x - b.x, y - b.y); }
Point operator+(const Point &b) const { return Point(x + b.x, y + b.y); }
//叉积
double operator^(const Point &b) const { return x * b.y - y * b.x; }
//点积
double operator*(const Point &b) const { return x * b.x + y * b.y; }
//返回两点的距离
double dist(Point p) { return hypot(x - p.x, y - p.y); }
//计算pa和pb的夹角, 就是求这个点看a,b 所成的夹角的弧度
double rad(Point a, Point b) {
Point p = *this;
return fabs(atan2(fabs((a - p) ^ (b - p)), (a - p) * (b - p)));
}
};
struct Line {
Point s, e;
Line() {}
// 两点确定一条线段
Line(Point _s, Point _e) {
s = _s;
e = _e;
}
//返回点和直线(方向向量)关系
// 1 在左侧; 2 在右侧; 3 在直线上
int relation(Point p) {
int c = sgn((p - s) ^ (e - s));
if (c < 0)
return 1;
else if (c > 0)
return 2;
else
return 3;
}
//两线段相交判断:规范相交:交点不在端点
// 2 规范相交;1 非规范相交;0 不相交
int segcrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
int d3 = sgn((v.e - v.s) ^ (s - v.s));
int d4 = sgn((v.e - v.s) ^ (e - v.s));
if ((d1 ^ d2) == -2 && (d3 ^ d4) == -2) return 2;
return (d1 == 0 && sgn((v.s - s) * (v.s - e)) <= 0) ||
(d2 == 0 && sgn((v.e - s) * (v.e - e)) <= 0) ||
(d3 == 0 && sgn((s - v.s) * (s - v.e)) <= 0) ||
(d4 == 0 && sgn((e - v.s) * (e - v.e)) <= 0);
}
bool parallel(Line v) { return sgn((e - s) ^ (v.e - v.s)) == 0; }
//求两直线的交点
//要保证两直线不平行或重合
Point crosspoint(Line v) {
double a1 = (v.e - v.s) ^ (s - v.s);
double a2 = (v.e - v.s) ^ (e - v.s);
return Point((s.x * a2 - e.x * a1) / (a2 - a1),
(s.y * a2 - e.y * a1) / (a2 - a1));
}
double length() { return s.dist(e); }
//点到直线的距离
double dispointtoline(Point p) {
return fabs((p - s) ^ (e - s)) / length();
}
//点到线段的距离
double dispointtoseg(Point p) {
if (sgn((p - s) * (e - s)) < 0 || sgn((p - e) * (s - e)) < 0)
return min(p.dist(s), p.dist(e));
return dispointtoline(p);
}
//直线和线段相交判断
//-*this line -v seg
// 2 规范相交
// 1 非规范相交
// 0 不相交
int linecrossseg(Line v) {
int d1 = sgn((e - s) ^ (v.s - s));
int d2 = sgn((e - s) ^ (v.e - s));
if ((d1 ^ d2) == -2) return 2;
return (d1 == 0 || d2 == 0);
}
};
Line l[N];
double rx, ry, r;
bool is_convex_hull(){
double base = 0.0;
for (int i = 1; i <= n;i++){
double temp = sgn((l[i].s - l[i].e) ^ (l[i - 1].e - l[i - 1].s));
if(!base)
base = temp;
if((sgn(base*temp))<0){
return false;
}
}
return true;
}
bool is_in_convex_hull(){
double temp = 0.0;
for (int i = 0; i < n;i++){
temp += Point(rx, ry).rad(l[i].e, l[i].s);
}
if(sgn(temp)==0) //点在外部
return false;
else if(sgn(temp+pi)==0||sgn(temp-pi)==0){ //点在边上,不包括顶点
if(sgn(r)==0)
return true;
}
else if(sgn(temp+2*pi)==0||sgn(temp-2*pi)==0) //点在内部
return true;
else{ //点在顶点上
if(sgn(r)==0)
return true;
}
return false;
}
bool round_in_convex_hull(){
for (int i = 0; i <= n;i++){
if(sgn(l[i].dispointtoline(Point(rx,ry))-r)<0)
return false;
}
return true;
}
int main(){
while (scanf("%d", &n) && (n >= 3)) {
scanf("%lf%lf%lf", &r,&rx, &ry);
double x1, y1, x0, y0,x2,y2;
scanf("%lf%lf", &x1, &y1);
x0 = x1, y0 = y1;
for (int i = 0; i < n-1;i++){
scanf("%lf%lf", &x2, &y2);
l[i] = Line(Point(x2, y2), Point(x1, y1));
x1 = x2, y1 = y2;
}
l[n-1]=Line(Point(x0, y0), Point(x2, y2));
l[n] = l[0];//多加一条边,方便操作
if(!is_convex_hull()){
printf("HOLE IS ILL-FORMED\n");
continue;
}
if(!is_in_convex_hull()){
printf("PEG WILL NOT FIT\n");
continue;
}
if (!round_in_convex_hull()){
printf("PEG WILL NOT FIT\n");
continue;
}
printf("PEG WILL FIT\n");
}
}
一组数据(来自:https://www.cnblogs.com/lyy289065406/archive/2011/07/31/2122829.html)
Sample Input
5 1.5 1.5 2.0
1.0 1.0
2.0 2.0
1.75 2.0
1.0 3.0
0.0 2.0
5 1.5 1.5 2.0
1.0 1.0
2.0 2.0
1.75 2.5
1.0 3.0
0.0 2.0
3 0.1 0.2 0.0
-0.5 1.0
0.5 -1.0
0.5 1.0
3 0.25 0.2 0.0
-0.5 1.0
0.5 -1.0
0.5 1.0
3 0.1 1.6 1.2
1.0 1.0
2.0 1.0
1.0 2.0
6 0.1 1.6 1.2
1.0 1.0
1.5 1.0
2.0 1.0
1.2 1.8
1.0 2.0
1.0 1.5
3 0.1 2.0 2.0
1.0 1.0
2.0 1.0
1.0 2.0
4 1.0 2.0 1.0
0.0 0.0
0.0 4.0
4.0 4.0
4.0 0.0
4 1.0 3.5 1.0
0.0 0.0
0.0 4.0
4.0 4.0
4.0 0.0
4 0.2 1.5 1.0
1.0 1.0
2.0 2.0
1.0 3.0
0.0 2.0
4 0.4 1.5 1.0
1.0 1.0
2.0 2.0
1.0 3.0
0.0 2.0
5 0.2 1.5 2.5
1.0 1.0
2.0 2.0
1.75 2.75
1.0 3.0
0.0 2.0
5 0.2 1.5 2.5
1.0 1.0
2.0 2.0
1.75 2.5
1.0 3.0
0.0 2.0
9 0.2 0.5 2.5
0.0 0.0
1.0 0.0
1.0 1.0
2.0 1.0
2.0 0.0
3.0 0.0
3.0 5.0
1.5 5.0
0.0 5.0
9 0.2 0.5 2.5
0.0 0.0
1.0 0.0
1.0 -1.0
2.0 -1.0
2.0 0.0
3.0 0.0
3.0 5.0
1.5 5.0
0.0 5.0
7 0.2 0.5 2.5
0.0 0.0
1.0 0.0
2.0 0.0
3.0 0.0
3.0 5.0
1.5 5.0
0.0 5.0
4 0.1 1 0.5
0 2
1 0
2 2
1 1
1
Sample Output
HOLE IS ILL-FORMED
PEG WILL NOT FIT
PEG WILL FIT
PEG WILL NOT FIT
PEG WILL FIT
PEG WILL FIT
PEG WILL NOT FIT
PEG WILL FIT
PEG WILL NOT FIT
PEG WILL NOT FIT
PEG WILL NOT FIT
PEG WILL FIT
PEG WILL NOT FIT
HOLE IS ILL-FORMED
HOLE IS ILL-FORMED
PEG WILL FIT
HOLE IS ILL-FORMED
标签:sgn,专题,return,Point,int,double,kuangbin,几何,include 来源: https://www.cnblogs.com/dyhaohaoxuexi/p/14123182.html