首页 > 其他分享> > 均方误差损失函数

均方误差损失函数

2020-11-28 14:03:51 作者：互联网

假设我们的模型是二维平面的线性回归模型： $h_{\theta}(x_i)=\theta_0+\theta_1x$ ，对于这个模型，我们定义损失函数为MSE，将得到如下的表达式：

下面我们试着通过概率的角度，推导出上述的MSE损失函数表达式。

在线性回归模型中，我们最终希望对于输入 $X$ 进行线性组合得到值Y，考虑到输入带有噪声的情况的表达式如下：

$Y=\theta_0+\theta_1x+\eta \\$

为了使模型更合理，我们假设 $\eta$ 服从均值为0，方差为1的高斯分布，即 $\eta\sim N(0,1)$ 。所以有：

$E[Y]=E[\theta_0+\theta_1x+\eta]=\theta_0+\theta_1x \\$

$Var[Y]=Var[\theta_0+\theta_1x+\eta]=1 \\$

所以，Y服从均值为 $\theta_0+\theta_1x$ ，方差为1的高斯分布，则样本点的 $(xi,yi)$ 概率为：

$p(y_i|x_i)=e^{-\frac{(yi-(\theta_0+\theta_1x_i))^2}{2}} \\$

有了单个样本的概率，我们就可以计算样本集的似然概率，我们假设每个样本是独立的：

$L(x,y)=\prod_{i=1}^Ne^{-\frac{(y_i-(\theta_0+\theta_1x_i))^2}{2}} \\$

对似然函数取对数，得到对数似然函数：

$l(x,y)=-\frac{1}{2}\sum_{i=1}^N(y_i-(\theta_0+\theta_1x_i))^2 \\$

这个对数似然函数的形式和我们的MSE损失函数的定义是一样的。所以，使用MSE损失函数意味着，我们假设我们的模型是对噪声的输入做估计，该噪声服从高斯分布。

缺点

使用MSE的一个缺点就是其偏导值在输出概率值接近0或者接近1的时候非常小，这可能会造成模型刚开始训练时，偏导值几乎消失。

假设我们的MSE损失函数为： $J = \frac{1}{2}(y_i - \hat{y_i})^2$ ，偏导为： $\frac{dJ}{dW} = (y_i - \hat{y_i})\sigma'(Wx_i + b)x_i$ ，其中 $\sigma'(Wx_i + b)$ 为 $\sigma(Wx_i + b)(1 - \sigma(Wx_i + b))$ 。可以看出来，在 $\sigma(Wx_i + b)$ 值接近0或者1的时候， $\frac{dJ}{dW}$ 的值都会接近于0，其函数图像如下：

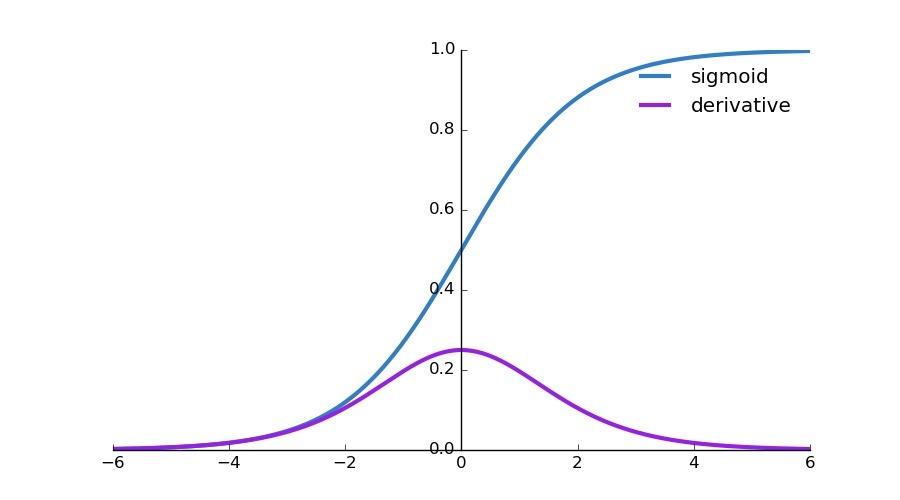
这导致模型在一开始学习的时候速率非常慢，而使用交叉熵作为损失函数则不会导致这样的情况发生。

ref:https://zhuanlan.zhihu.com/p/35707643（致敬原作者）

标签：似然,误差,函数,模型,均方,损失,MSE,高斯分布
来源： https://www.cnblogs.com/xiaoxiaomajinjiebiji/p/14052345.html