SPFA

简单介绍一下\(SPFA\)：先把所有点的值赋为INF，然后找到起点，标位零，将其压入队列（都到这里了，应该没人不会队列了吧…），下面的步骤要循环经行，直到队列为空。找到延生出来的节点，如果节点的值大于当前的点的值加边的长度（设当前节点的值是\(v_i\)，延伸出来的点的值是\(v_j\)，边的长度是\(d_i\)，则上面那句话的意思是如果\(v_i\)+\(d_i\)>\(v_j\)），就更新并加入队列。
具体实现就是这个亚子：

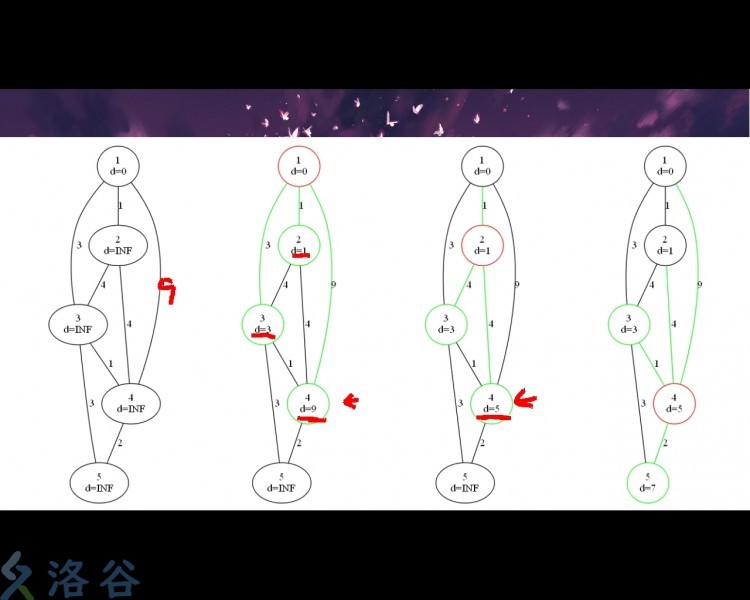
看到第三幅图的那个箭头了吗？那里是不能加入队列的，因为队列里已经有4号点了，这是\(SPFA\)最容易打错的地方。

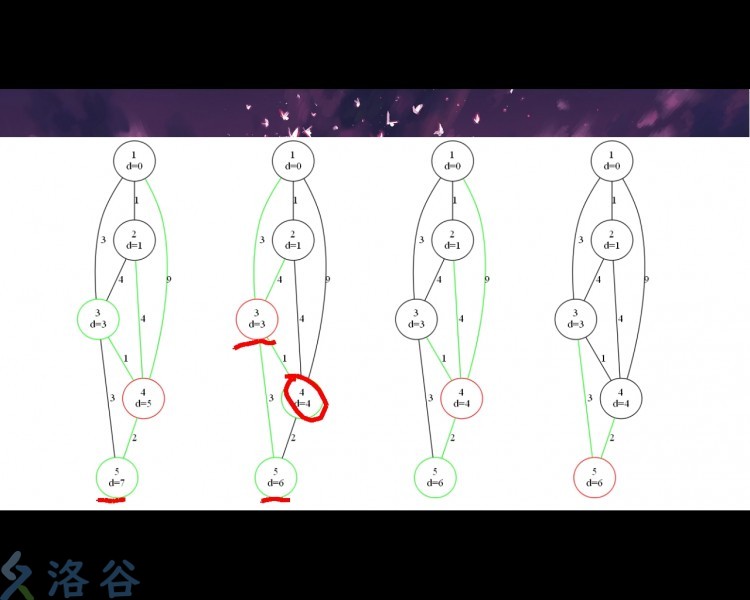
（图片来源于洛谷2019夏令营的课件）
这里再说一下有关\(SPFA\)的其他的东西：

1. 上面更新点的最短路的操作称为松弛操作
2. \(SPFA\)可以有负权边，但\(dij\)不行
3. \(SPFA\)也可以判负权环，就是一个点被松弛了n次，该题没有负权环，因为负权环会使最短路无限小，而题面没有给出处理方法

接下来是最激动人心的时刻：上代码！！！

#include<bits/stdc++.h>
using namespace std;
int n,m,s;
queue<int>q;
bool f[10005];//用于标记是否加入队列
int v[10005];//每个点离起点的最短路径
struct graph
{
	int tot;
	int hd[10005];
	int nxt[500005],to[500005],dt[500005];
	void add(int u,int v,int w)
	{
		tot++;
		nxt[tot]=hd[u];
		hd[u]=tot;
		to[tot]=v;
		dt[tot]=w;
		return ;
	}
}g;
int main()
{
	scanf("%d%d%d",&n,&m,&s);
	for(int i=1;i<=m;i++)
	{
		int u,v,w;
		scanf("%d%d%d",&u,&v,&w);
		g.add(u,v,w);
	}
	memset(v,0x3f,sizeof(v));//初始化，初始化必须是一个很大的值，否则如果实际路径比初始化长就会出问题
	v[s]=0;
	f[s]=true;
	q.push(s);
	while(!q.empty())//直到队列为空为止
	{
		int xx=q.front();
		q.pop();//取出第一个元素并弹出
		f[xx]=false;//标记为没有加入队列
		for(int i=g.hd[xx];i;i=g.nxt[i])//枚举该节点延伸出来的点
			if(v[g.to[i]]>v[xx]+g.dt[i])//松弛操作
			{
	 			if(!f[g.to[i]]) q.push(g.to[i]),f[g.to[i]]=true;//加入队列
				v[g.to[i]]=v[xx]+g.dt[i];//更新
			}
	}
	for(int i=1;i<=n;i++)
		if(v[i]!=1e10) printf("%d ",v[i]);
		else printf("2147483647 ");
	return 0;
}

标签：int,tot,队列,SPFA,dt,负权
来源： https://www.cnblogs.com/mk-oi/p/14014524.html