首页 > 其他分享> > 【题解】引水入城

【题解】引水入城

2020-10-31 07:31:36 作者：互联网

引水入城题解

NOIp2010T4 题解

首先，这是本人的第一道独立AC的蓝题

part1.N==1(10pts)

$n==1$时，只有一排城市，这一排城市既临湖又临沙漠。
那么，易得一定有合法方案。而且只需找出这一排高度极大值山顶或平台都有蓄水场就能满足要求。（要注意端点也要考虑）
易得：如果我们把$mp_{1,0}$和$mp_{1,m}$都赋值为$0$，那么只需在$mp_{1,i}>mp_{1,i-1}\&\&mp_{1,i}>mp_{1,i+1}$时需要在该点建蓄水厂，否则，该点一定可以被其他城市流出的水流经，无需再建蓄水厂。

code 10pts

#include<cstdio>
#include<iostream>
using namespace std;
const int N=505;
int n,m;
int mp[N][N],up[N],ans;

int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&mp[i][j]);
    if(n==1)
    {
        for(int i=1;i<=m;i++)
            if(mp[1][i]>=mp[1][i-1]&&mp[1][i]>=mp[1][i+1])
                ans++;
        printf("%d\n%d",1,ans);
        return 0;
    }
}

part2.无解(30pts)

只需要以第一行的每一个点为起点跑一次BFS，对跑到的每一个点打标记，最后统计最后一行没有标记的点，如果存在这样的点，$ans++$; 如果最后$ans$不为零，第一行输出$0$，第二行输出$ans$；反之，第一行输出$1$，然后输出随机数（大雾

code 10pts+30pts=40pts

#include<queue>
#include<cstdio>
#include<iostream>
using namespace std;
int m,n;
const int N=505;
int mp[N][N],hi[N],vis[N][N],cnt,num;
int sum,ans;
int dir1[]={0,0,0,1,-1};
int dir2[]={0,1,-1,0,0};
struct node
{
    int x,y;
};
queue<node>q;
void bfs(int x,int y)
{
    q.push((node){x,y});vis[x][y]=1;
    while(!q.empty())
    {
        int x=q.front().x,y=q.front().y;q.pop();
        for(int i=1;i<=4;i++)
        {
            if(x+dir1[i]>n||x+dir1[i]<1||y+dir2[i]>m||y+dir2[i]<1)
                continue;
            if(vis[x+dir1[i]][y+dir2[i]]) continue;
            if(mp[x+dir1[i]][y+dir2[i]]<mp[x][y])
                q.push((node){x+dir1[i],y+dir2[i]}),vis[x+dir1[i]][y+dir2[i]]=1;
        }
    }
}
int main()
{
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&mp[i][j]);
    if(n==1)
    {
        for(int i=1;i<=m;i++)
            if(mp[1][i]>=mp[1][i-1]&&mp[1][i]>=mp[1][i+1])
                ans++;
        printf("%d\n%d",1,ans);
        return 0;
    }
    for(int i=1;i<=m;i++)
        if(mp[1][i]>=mp[1][i-1]&&mp[1][i]>=mp[1][i+1])
            hi[++cnt]=i,bfs(1,i);
    for(int i=1;i<=m;i++)
        if(!vis[n][i]) sum++;
    if(sum)
    {
        printf("%d\n%d",0,sum);
        return 0;
    }
}

part3.正解

经过分析，我发现每个起点对应的最后行的区间是确定的，所以我就突发奇想：是不是所有点对应的区间都是一段？结果，我还真就证明出来了$\dotsb$
证明过程如下:

我们用反证法。假设我上面的观点是错误的，那么就会出现这样的一个点和它的水的流法

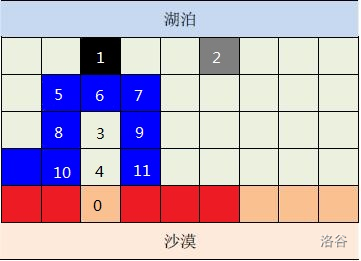
~~由几何关系得~~
如上图，黑色方块表示起始点$1$，及对应两个区间的起始点，则由题意得：由$5,6,7,8,9,10$号点中的任意一个都不能流到$0$号点
因为保证所有点一定能被经过，所以一定存在起始点$2$（灰色方块）流经$0$号点。
然鹅由于$2$号点位于$5,6,7,8,9,10$号点围成的圈的外面，所以该起始点出发的水一定经$5,6,7,8,9,10$号点中的至少一个流到$0$号点，与上面得到的结论矛盾，所以要证明的观点是正确的。
证毕

所以该问题就转化为了给定几个小区间，求将整个大区间都覆盖需要的最小区间数量。
这个问题十分经典，学名叫区间覆盖（也叫线段覆盖）。
区间覆盖模板（把最少变成了最多）
所以说我们要怎么解决呢？

区间dp

首先，由于这是一个区间问题，所以我们自然而然就会想到区间$dp$
用区间$dp$思维难度极低，~~有脑子就行~~
状态设计：
我们用$dp_{i,j}表示从$i$到$j$最少需要的线段数量

状态转移：
我想不用说大家都已经明白了

dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]);

时间复杂度：$\theta(m^3)$
过不了模板，但这道题…m<=500,m^3<=1.25e8 好像不行$\dotsb$
但是

在NOIp，数据是很水的 ——byGroup_1

话又说回来，这道题预处理都要
$\theta(m^2*n)$，还在意这点复杂度？

code 区间dp

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
int m,n;
const int N=505;
int mp[N][N],hi[N],vis[N][N],cnt,num;
int dp[N][N];
int sum,ans;
int dir1[]={0,0,0,1,-1};
int dir2[]={0,1,-1,0,0};
struct node
{
    int x,y;
};
queue<node>q;
void bfs(int x,int y)
{
    q.push((node){x,y});vis[x][y]=1;
    while(!q.empty())
    {
        int x=q.front().x,y=q.front().y;q.pop();
        for(int i=1;i<=4;i++)
        {
            if(x+dir1[i]>n||x+dir1[i]<1||y+dir2[i]>m||y+dir2[i]<1)
                continue;
            if(vis[x+dir1[i]][y+dir2[i]]) continue;
            if(mp[x+dir1[i]][y+dir2[i]]<mp[x][y])
                q.push((node){x+dir1[i],y+dir2[i]}),vis[x+dir1[i]][y+dir2[i]]=1;
        }
    }
}
int main()
{
//    freopen("C:/Users/.D043/Desktop/P1514_2.in","r",stdin);
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&mp[i][j]);
    if(n==1)
    {
        for(int i=1;i<=m;i++)
            if(mp[1][i]>=mp[1][i-1]&&mp[1][i]>=mp[1][i+1])
                ans++;
        printf("%d\n%d",1,ans);
        return 0;
    }
    for(int i=1;i<=m;i++)
        if(mp[1][i]>=mp[1][i-1]&&mp[1][i]>=mp[1][i+1])
            hi[++cnt]=i,bfs(1,i);
    for(int i=1;i<=m;i++)
        if(!vis[n][i]) sum++;
    if(sum)
    {
        printf("%d\n%d",0,sum);
        return 0;
    }
    memset(dp,0x3f,sizeof(dp));
    for(int i=1;i<=cnt;i++)
    {
        memset(vis,0,sizeof(vis));
        bfs(1,hi[i]);
        int l,r;
        for(int k=1;k<=m;k++)
        {
            if(vis[n][k]&&!vis[n][k-1]) l=k;
            if(vis[n][k]&&!vis[n][k+1])
            {
                r=k;break;
            }
        }
        for(int k=l;k<=r;k++)
            for(int j=l;j<=k;j++)
                    dp[j][k]=1;
    }
    for(int l=2;l<=m;l++)
    {
        for(int i=1;;i++)
        {
            int j=i+l-1;
            if(j>m) break;
            for(int k=i;k<=j;k++)
                dp[i][j]=min(dp[i][j],dp[i][k]+dp[k+1][j]);
        }
    }
    printf("%d\n%d",1,dp[1][m]);
    return 0;
}

贪心

~~贪心我就不加赘述了，好，过~~
贪心方案：
从左端点已经被覆盖的区间中取右端点最靠右的区间
先上代码
代码片段

int rg=0,st=1;ans=0;
while(rg<m)
{
    int x=rg;
    for(int i=st;i<=cnt;i++)
    {
        if(l[i]>rg+1)
        {
            st=i;break;
        }
        else x=max(x,r[i]);
    }
    ans++,rg=x;
}
//rg:已覆盖区间右端点
//st:已枚举区间最大的左端点
//ans:最少的区间数量

关于正确性

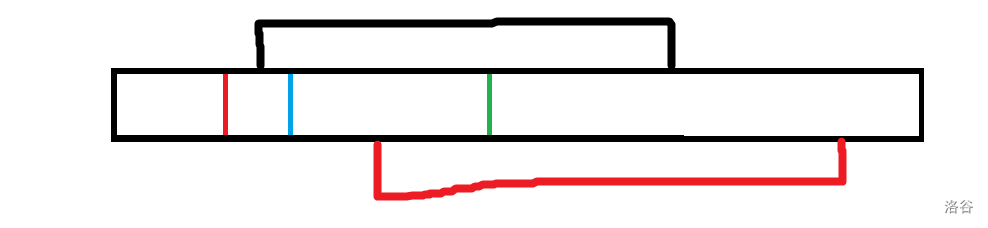
我们以上图为例：用红色表示当前已覆盖过的右端点，蓝色和绿色表示左端点已被覆盖的右端点值
用黑色和红色分别代表后几个区间

如果是黑色的情况，则绿色不会比蓝色更劣
如果是红色的情况，则绿色比蓝色更优

综上，无论什么情况，选择右端点更靠右的一定不比靠左的更劣
证毕
code

#include<queue>
#include<cstdio>
#include<cstring>
#include<iostream>
using namespace std;
int m,n;
const int N=505;
int mp[N][N],hi[N],vis[N][N],cnt,num;
int sum,ans;
int l[N],r[N];
int dir1[]={0,0,0,1,-1};
int dir2[]={0,1,-1,0,0};
struct node
{
    int x,y;
};
queue<node>q;
void bfs(int x,int y)
{
    q.push((node){x,y});vis[x][y]=1;
    while(!q.empty())
    {
        int x=q.front().x,y=q.front().y;q.pop();
        for(int i=1;i<=4;i++)
        {
            if(x+dir1[i]>n||x+dir1[i]<1||y+dir2[i]>m||y+dir2[i]<1)
                continue;
            if(vis[x+dir1[i]][y+dir2[i]]) continue;
            if(mp[x+dir1[i]][y+dir2[i]]<mp[x][y])
                q.push((node){x+dir1[i],y+dir2[i]}),vis[x+dir1[i]][y+dir2[i]]=1;
        }
    }
}
int main()
{
//    freopen("C:/Users/.D043/Desktop/P1514_2.in","r",stdin);
    scanf("%d%d",&n,&m);
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++)
            scanf("%d",&mp[i][j]);
    for(int i=1;i<=m;i++)
        if(mp[1][i]>=mp[1][i-1]&&mp[1][i]>=mp[1][i+1])
            hi[++cnt]=i,bfs(1,i);
    for(int i=1;i<=m;i++)
        if(!vis[n][i]) sum++;
    if(sum)
    {
        printf("%d\n%d",0,sum);
        return 0;
    }
    for(int i=1;i<=cnt;i++)
    {
        memset(vis,0,sizeof(vis));
        bfs(1,hi[i]);
        for(int k=1;k<=m;k++)
        {
            if(vis[n][k]&&!vis[n][k-1])
                l[i]=k;
            if(vis[n][k]&&!vis[n][k+1])
            {
                r[i]=k;break;
            }
        }
    }
    int rg=0,st=1;ans=0;
    while(rg<m)
    {
        int x=rg;
        for(int i=st;i<=cnt;i++)
        {
            if(l[i]>rg+1)
            {
                st=i;break;
            }
            else x=max(x,r[i]);
        }
        ans++,rg=x;
    }
    printf("%d\n%d",1,ans);
    return 0;
}

本篇题解::`return 0;`

标签：int,题解,mp,ans,区间,引水,include,dp
来源： https://www.cnblogs.com/why-Y/p/13905086.html