[五年CSP三年模拟]洛谷2020初赛模拟赛分析
作者:互联网
单项选择题
第1题
题面
1.十进制数 \(114\) 的相反数的 \(8\) 位二进制补码是:
A.10001110\(\qquad\)B.10001101
C.01110010\(\qquad\)D.01110011
分析与解答
\(114\) 的相反数为 \(-114\),
\(-114\) 的二进制原码为 \(11110010\)
所以它的补码为原码按位取反加一
即为 \(10001110\),选 A.
第2题
题面
2.以下哪个网站不是 Online Judge (在线程序判题系统)? Online Judge可以查看算法题目,提交自己编写的程序,然后可以获得评测机反馈的结果。
A.Luogu\(\qquad\)B.Gitee\(\qquad\)C.Leetcode\(\qquad\)D.Codeforces
分析与解答
不多BB,自己点进去看[\doge]
第3题
题面
小A用字母 \(A\) 表示 \(1\),用 \(B\) 表示 \(2\),以此类推,用 \(Z\) 表示 \(26\)。对于 \(27\) 以上的数字,可以用两位或者更长的字符串对应,例如 \(AA\) 表示 \(27\),\(AB\) 表示 \(28\),\(AZ\) 对应 \(52\),\(AAA\) 对应 \(703\)……那么 \(BYT\) 字符串对应的数字是什么?
A.2018\(\qquad\)B.2020\(\qquad\)C.2022\(\qquad\)D.2024
分析与解答
我们发现,我们可以把它看成一种特殊的27进制数,这种数没有 '0' 这个数字,打个比方,就像十进制数 '9' 之后直接是 '11','99' 之后直接是 '111',即第二位向第三位进一时需要的数不用加上第一位的 26 ,那么我们可以发现,每 \(27\) 向第二位进一,但上一位需保留 \(1\)(所以第二位每一个一只包含26),每 \(26^2\) 向第三位进一
通过推算可以得到下表
| Str | Num | Str* |
|---|---|---|
| A | 1 | \(1\) |
| Z | 26 | \(Z\) |
| AA | 27 | \(Z + 1\) |
| AZ | 52 | \(Z + Z\) |
| BA | 53 | \(Z + Z + 1\) |
| ZZ | 702 | \(26^2 + Z\) |
| AAA | 703 | \(ZZ + 1\) |
| AZZ | 1378 | \(ZZ + 26^2\) |
| BZZ | 2054 | \(ZZ + 2 \times 26^2\) |
| BYZ | 2038 | \(ZZ + 2 \times 26^2 - Z\) |
| BYT | 2022 | \(ZZ + 2 \times 26^2 - Z - 16\) |
故选 B.
第4题
题面
分析与解答
图片大小计算公式:
\[图片大小=\dfrac{分辨率(长 \times 宽) \times 位深}{8} \]这张图片的大小为:
\[\begin{align*} &\dfrac{4096 \times 2160 \times 24}{8} B\\ =&(1024 \times 1080 \times 24) B\\ =&(1080 \times 24) KB\\ \approx & 25MB \end{align*}\]故选 B.
第5题
题面
分析与解答
最快的排序为 桶排序,时间复杂度为 \(O(n)\),故选 A.
第6题
题面
分析与解答
树是一个简单无环连通图,故①④错
选 C.
第7题
题面
分析与解答
每次分成两堆,每张卷子至少查看两次,故为 \(42 \times 2=84\) 次
故选 A.
第8题
题面
分析与解答
- 前序遍历(VLR)是二叉树遍历的一种,也叫做先根遍历、先序遍历、前序周游,可记做根左右。前序遍历首先访问根结点然后遍历左子树,最后遍历右子树。
- 中序遍历(LDR)是二叉树遍历的一种,也叫做中根遍历、中序周游。在二叉树中,中序遍历首先遍历左子树,然后访问根结点,最后遍历右子树。
由以上的定义我们可以很轻松的画出这棵树:
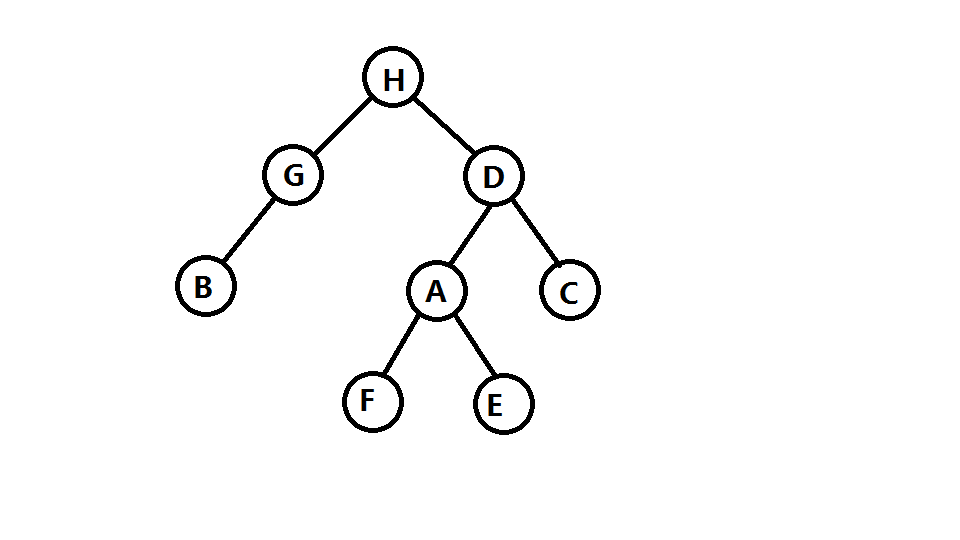
我们又知道,二叉树中,结点 \(i\) 的左儿子编号为 \(2 \times i\),右儿子编号为 \(2 \times i+1\),
故可得下图
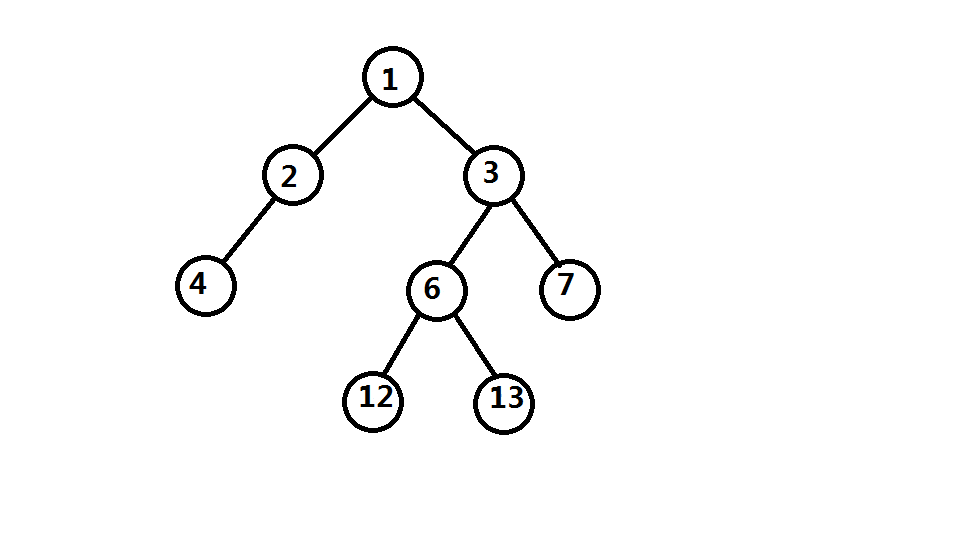
所以数组最大下标为 \(13\)
故选 B.
第9题
题面
分析与解答
优先级: \(! > \&\& > ||\)
A选项:\(a\&\&b=0\),\(b\&\&c=0\),所以 \(0||0=0\)
B选项:\(a+b>c=0\),\(b=0\),所以 \(0||0=0\)
C选项:\(!c=0\),\(!a||b=0\),所以 \(0||0=0\)
D选项:\(a+b+c=2\),C艹C++中bool运算非0即
故选 D.
第10题
题面
分析与解答
链表的查询是由前向后逐个查找,那么查询次数最少的情况就是每次要查找的数都是链表的头结点,每次只访问一个结点,共有 \(k\) 次请求,故为 \(k\) 次
故选 B.
第11题
题面
分析与解答
- 枚举大法
这显然是道排列组合,不过数据较小,可以枚举(枚举大法好)
要注意每个班有人数限制
| i | C | B | A |
|---|---|---|---|
| 1 | 0 | 0 | 5 |
| 2 | 0 | 2 | 4 |
| 3 | 0 | 3 | 3 |
| 4 | 0 | 4 | 2 |
| 5 | 1 | 0 | 5 |
| 6 | 1 | 1 | 4 |
| 7 | 1 | 2 | 3 |
| 8 | 1 | 3 | 2 |
| 9 | 1 | 4 | 1 |
| 10 | 2 | 0 | 4 |
| 11 | 2 | 1 | 3 |
| 12 | 2 | 2 | 2 |
| 13 | 2 | 3 | 1 |
| 14 | 2 | 4 | 0 |
| 15 | 3 | 0 | 3 |
| 16 | 3 | 3 | 0 |
| 17 | 3 | 1 | 2 |
| 18 | 3 | 2 | 1 |
共 \(18\) 种
- 排列组合
我们可以将这个问题看成 “有 \(6\) 个相同的小球,放进 \(3\) 个不相同的的盒子中,每个盒子有限制,可以为空”,
我们先来求 “有 \(6\) 个相同的小球,放进 \(3\) 个不相同的的盒子中,可以为空” 的所有情况,即
其中 “有一个盒子中有 \(6\) 个小球,其余盒子为空” 的 \(3\) 种情况都无法满足条件
“有一个盒子中有 \(5\) 个小球,其余两个盒子中,有一个盒子里有 \(1\) 个球”的情况下,这 \(5\) 个球在B盒或C盒的 \(2 \times 2=4\) 种情况无法满足条件
对于每个盒子,盒子里有 \(5\) 个球时,都有 \(2\) 种情况,为
1 5 0,0 5 1和0 1 5,1 0 5
“有一个盒子中有 \(4\) 个小球,其余 \(2\) 个球分散在剩下两个盒子里” 的情况下,这 \(4\) 个球在C盒的 \(C^1_3=3\) 种情况(4 0 2,4 2 0,4 1 1)无法满足条件
那么共有 \(28 - 3 - 4 - 3 = 18\) 种情况
故选 B.
第12题
题面
分析与解答
各排序时间复杂度(平均):
- 插入排序 \(O(n^2)\)
- 希尔排序 \(O(n^{1.3})\)
- 选择排序 \(O(n^2)\)
- 堆排序 \(O(n\log{n})\)
- 冒泡排序 \(O(n^2)\)
- 快速排序 \(O(n\log{n})\)
- 归并排序 \(O(n\log{n})\)
- 基数排序 \(O(d(r+n))\)(\(d\) 表示长度,\(r\) 表示关键字基数,\(n\) 表示关键字个数)
故选 B.
第13题
题面
分析与解答
\(x \in [a,b)\) 表示 \(a \leqslant x < b\)
rand()%M表示生成一个在区间 \([0,M)\) 内的随机数
所以rand()%M+a可生成一个在区间 \([a,M+a)\) 内的随机数
那么生成一个在区间 \([a,b)\) 内的随机数就等价于生成一个在区间 \([a,b-a+a)\) 内的随机数
即为rand()%(b-a)+a
故选 A.
第14题
题面
分析与解答
我们首先看森林和完全图的定义:
森林(forest)是 \(m\)(\(m \geqslant 0\))棵互不相交的树的集合。
完全图是一个简单的无向图,其中每对不同的顶点之间都恰连有一条边相连。
所以,只有一棵树也可以称作森林
那这道题就变成了 “一个7个顶点的完全图需要至少删掉多少条边才能变成一棵树?”
一个有7个顶点的完全图共有 \(\dfrac{7 \times (7-1)}{2}=21\)条边
一棵有7个结点的树共有 \(6\) 条边
所以最少删去 \(21-6=15\) 条边
故选 C.
第15题
题面
分析与解答
第37届全国青少年信息学奥林匹克竞赛(CCF NOI2020)于2020年8月16-21日在长沙市一中雨花新华都学校举行
故选 D.
阅读程序
第1题
#include<iostream>
using namespace std;
#define MAXN 20
int gu[MAXN][MAXN];
int luo(int n, int m) {
if(n <= 1 || m < 2)
return 1;
if(gu[n][m] != -1)
return gu[n][m];
int ans = 0;
for(int i = 0;i < m;i += 2)
ans += luo(n - 1,i);
gu[n][m] = ans;
return ans;
}
int main(){
int n, m;
cin >> n >> m;
for(int i = 0; i < MAXN; i++)
for(int j = 0; j < MAXN; j++)
gu[i][j] = -1;
cout << luo(n, m);
return 0;
}
1.luo函数中,\(m\) 的值不可能是奇数 ( )
在主程序main()中,传入luo(n,m),这里 \(m\) 的值由键盘输入,可以为奇数,故为错
2.若将第11行的 “<” 改为 “<=”,程序的输出结果可能会改变 ( )
改后可能会多循环一次,结果可能会改变,故为对
3.若将第8.9.13行删除,程序的运行的结果不变 ( )
观察程序可以发现,二维数组gu[i][j]是用作记忆化搜索
而第8.9.13行则是进行记忆化搜索的实现,记忆化搜索仅会减少程序运行的时间,但不会改变结果,故为对
4.在添加合适的头文件后,将第19到21行替换为memset(gu,255,sizeof(gu));可以起到相同的作用 ( )
第19到21行是给二维数组gu[i][j]赋初值 \(-1\),
memset() 是给每一个byte赋值
int是4 byte = 32bit
255的二进制是 11111111,但是当赋值给数组时以补码形式赋值,第一位是符号位,就变成了 \(-1\),故为对
5.若输入数据为 4 8,则输出为( )
A.7\(\qquad\)B.8\(\qquad\)C.15\(\qquad\)D.16
没什么好说的,要有一颗勇于模拟的心ヽ( ̄▽ ̄)و选B.
6.最坏情况下,此程序的时间复杂度是( )
A.\(O(m^2n)\qquad\)B.\(O(nm!)\qquad\)C.\(O(n^2)\qquad\)D.\(O(n^2m)\)
不会,过/kk 选 A.
第2题
1.错误
调整之后,f[i][k]和f[k][j] 可能并没有计算或得到的不是最优解,但只被计算2次,不能保证是全局最优解,而原程序则会计算多次,保证为最优解
2.错误
m与输入有关,想想为什么会有快读这个东西
3.正确
注意数据范围,当整个为一条链或数据足够大时,答案会超出 \(10^7\)
4.正确
两者顺序更换对答案并无影响
5.A
我们首先需要知道这个程序是在求什么,
第14到19行,求的是原图的任意两点间最短路长度
第21到40行,则是将原图中任意两点并为一点,再求出此时任意两点间最短路长度之和,取最小值,数据并不大,可以手动模拟
6.A
这奇妙的时间复杂度,肯定就是Floyd(。-`ω´-)
未完待续...
更新日志及说明
更新
- 初次完成编辑 - \(2020.10.9\)
本文若有更改或补充会持续更新
个人主页
欢迎到以下地址支持作者!
Github:戳这里
Bilibili:戳这里
Luogu:戳这里
标签:遍历,洛谷,题面,qquad,初赛,times,故选,模拟,解答 来源: https://www.cnblogs.com/Dfkuaid-210/p/13786364.html













