逛公园

题目描述

策策同学特别喜欢逛公园。公园可以看成一张 \(N\) 个点 \(M\) 条边构成的有向图，且没有自环和重边。其中 \(1\) 号点是公园的入口，\(N\) 号点是公园的出口，每条边有一个非负权值， 代表策策经过这条边所要花的时间。

策策每天都会去逛公园，他总是从 \(1\) 号点进去，从 \(N\) 号点出来。

策策喜欢新鲜的事物，它不希望有两天逛公园的路线完全一样，同时策策还是一个 特别热爱学习的好孩子，它不希望每天在逛公园这件事上花费太多的时间。如果 \(1\) 号点 到 \(N\) 号点的最短路长为 \(d\)，那么策策只会喜欢长度不超过 \(d+K\) 的路线。

策策同学想知道总共有多少条满足条件的路线，你能帮帮它吗？

为避免输出过大，答案对 \(P\) 取模。

如果有无穷多条合法的路线，请输出 \(−1\) 。

输入格式

第一行包含一个整数 \(T\)， 代表数据组数。

接下来 \(T\) 组数据，对于每组数据： 第一行包含四个整数 \(N,M,K,P\)，每两个整数之间用一个空格隔开。

接下来 \(M\) 行，每行三个整数 \(a_i,b_i,c_i\)​，代表编号为 \(a_i,b_i\) ​的点之间有一条权值为 \(c_i\) ​的有向边，每两个整数之间用一个空格隔开。

输出格式

输出文件包含 \(T\) 行，每行一个整数代表答案。

输入输出样例

输入 #1

2
5 7 2 10
1 2 1
2 4 0
4 5 2
2 3 2
3 4 1
3 5 2
1 5 3
2 2 0 10
1 2 0
2 1 0

输出 #1

3
-1

说明/提示

【样例解释1】

对于第一组数据，最短路为 \(3\)。 \(1-5,1-2-4-5,1-2-3-5\) 为 \(3\) 条合法路径。

【测试数据与约定】

对于不同的测试点，我们约定各种参数的规模不会超过如下

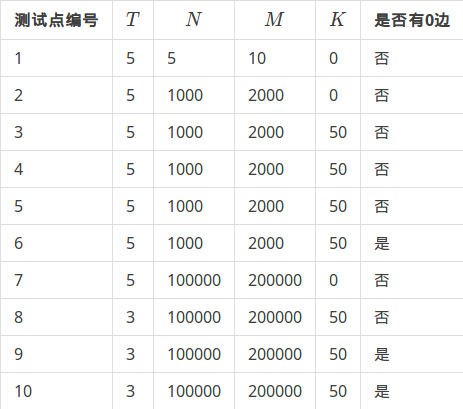
对于 \(100\%\) 的数据， \(1 \le P \le 10^9,1 \le a_i,b_i \le N ,0 \le c_i \le 1000\)。

数据保证：至少存在一条合法的路线。

思路

刚开始的求最短路不用说，\(SPFA\) 和 \(dijkstra\) 都可，不会有人真的以为这道题会卡 \(SPFA\) 吧，不会吧，不会吧。

先讨论一下 \(-1\) 的情况，为什么会出现无穷条路径？

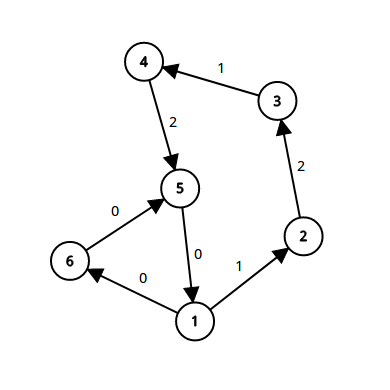
易证，当我们有 \(0\) 环的时候，我们就会在上图中的 \(1-6-5\) 这个环里一直走啊走啊走～～～

如果这个环的权值不为 \(0\)，是不是还是 \(-1\) 呢，显然不是的。

因为在这个环里走的话，你走的路径会越来越长，长度总有一刻会超过限制，所以路径是有限的。

---

处理完了特殊情况，路径数量怎么求呢？

如果你直接暴搜，恭喜您，您已经取得了 \(30opts\) 的好成绩，不过，您会 \(T\) 到飞起。

正解是什么呢？

首先，我们会发现，\(k\) 的

标签：le,NOIP,路径,整数,策策,逛公园,2017,号点
来源： https://www.cnblogs.com/Rubyonly233/p/13507456.html