基于JS的二维物理引擎--碰撞检测
作者:互联网
基于JS的二维物理引擎--碰撞检测
声明:本文中所用数学均为高一及以下学过的公式,图形部分均由几何画板完成
目录
一.圆与圆的碰撞检测
二.圆与正多边形的碰撞检测
(一)边界接触
(二)圆心的轨迹
(三)计算
(四)推广
(五)参考代码
三.总结
一.圆与圆的碰撞检测
圆与圆的碰撞检测很简单,就是圆与圆的相切问题
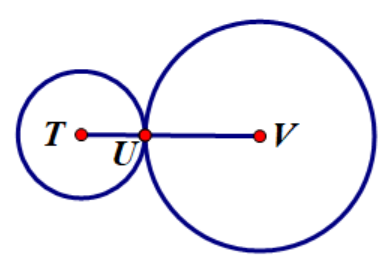
(图示1.1)
简言之就是两圆心距离小于等于两圆半径之和时,两物体处于碰撞状态
(代码)
二.圆与正多边形的碰撞检测
首先要明确的一点是,正多边形与圆的属性多了一些不同的地方,比如正多边形有角,圆没有角,所以在正多边形类中就要多出更多属性,那么更多属性该怎么存进类里面呢?
再研究一下圆和正多边形,我们会发现正多边形除了边更多了,其实其他属性都相差不大,而且边越多两者就越为接近,所以我选择了以下的储存方式
1 this.x = x 2 this.y = y 3 4 this.marginCount = marginCount//小于3均为圆形 5 this.size = size 6 this.round = marginCount < 3 ? 0 : round % (360 / marginCount) 7 this.roundPI = this.round * Math.PI / 180
将这个属性绘制到canvas上的代码
1 drawToCanvas(ctx) {//lineWidth是常数,为线宽
2 if ( !this.visible )
3 return
4
5 var unit = Math.PI / 180
6 ctx.beginPath()
7 if(this.marginCount < 3){
8 ctx.arc(this.x, this.y, this.size - lineWidth / 2, 0, 360 * unit)
9 }
10 else{
11 ctx.moveTo(
12 this.x + (this.size - lineWidth / 2) * Math.cos(this.round*unit),
13 this.y + (this.size - lineWidth / 2) * Math.sin(this.round*unit)
14 )
15 for(let i=1;i<=this.marginCount;++i)
16 ctx.lineTo(
17 this.x + (this.size - lineWidth / 2) * Math.cos((this.round+i*360/this.marginCount)*unit),
18 this.y + (this.size - lineWidth / 2) * Math.sin((this.round+i*360/this.marginCount)*unit)
19 )
20 }
21
22 ctx.closePath()
23 ctx.strokeStyle = this.color
24 ctx.lineWidth = lineWidth
25 ctx.stroke()
26 ctx.fillText(this.strength, this.x - 10, this.y + 5, 20)
27 }
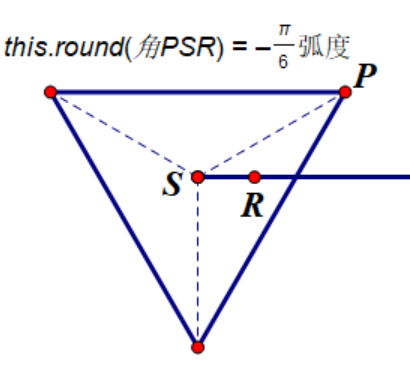
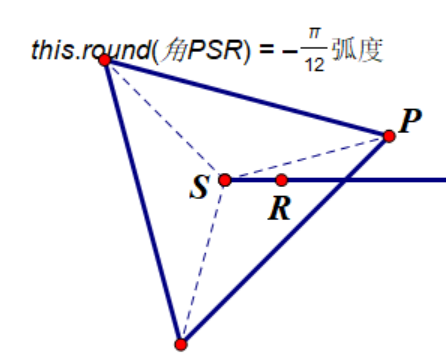
(正多边形属性对应图示2.1.1)(正多边形属性对应图示2.1.2)
优先考虑正多边形偏转角(this.round)为0的情况且边(this.marginCount)为3的情况,且已知圆与正多边形的xy坐标:
(一)边界接触
分解一下,圆和正多边形的边界接触可以分为两类:
1.边和圆接触
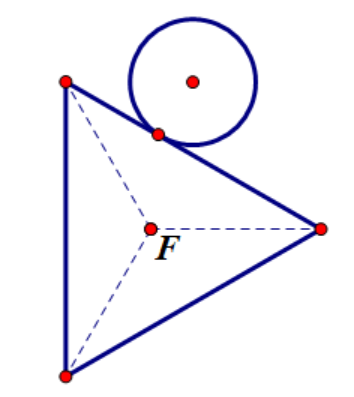
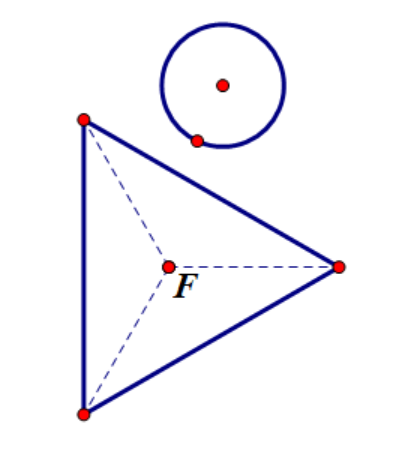
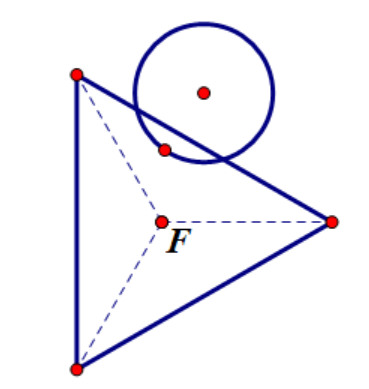
(接触图示2.2) (不接触图示2.3) (相交图示2.4)
所以只要把边界条件求出来即可,放大后(图2.5)就发现
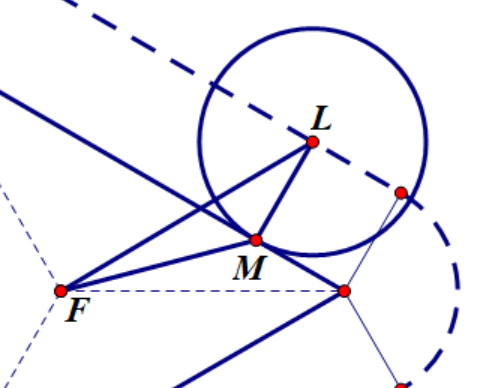
(放大图示2.5)
很明显是一个三角形问题,如何解我放在计算里面
2.角和圆接触
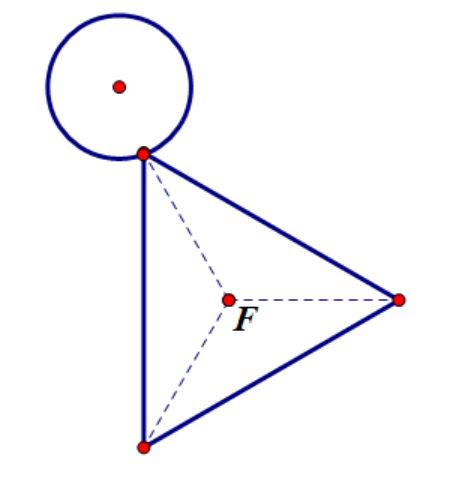
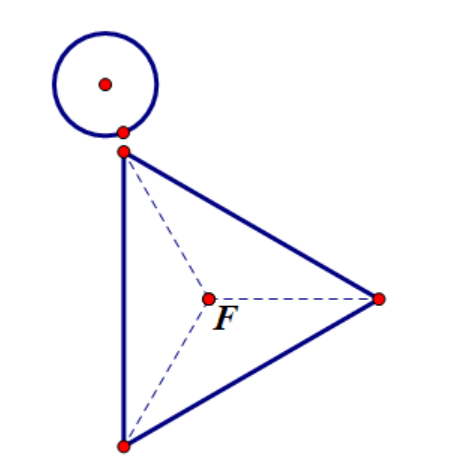
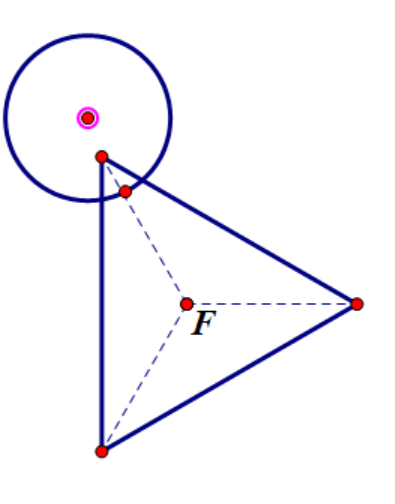
(接触图示2.6) (不接触图示2.7) (相交图示2.8)
同样放大后(图2.9)会发现是这样的
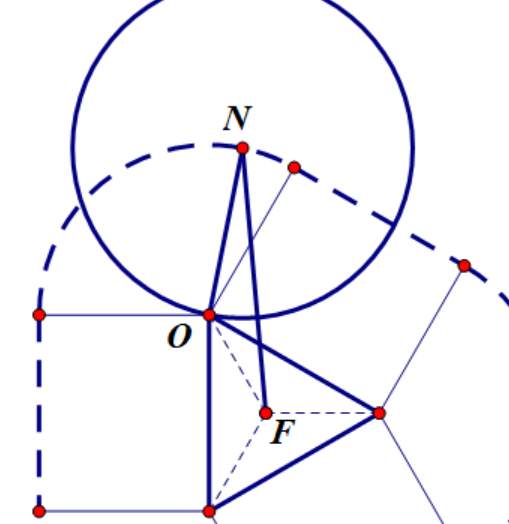
(放大图示2.9)
同样如何解我也放在计算里面
(二)边界条件里圆心的轨迹
角接触和边接触的分界条件
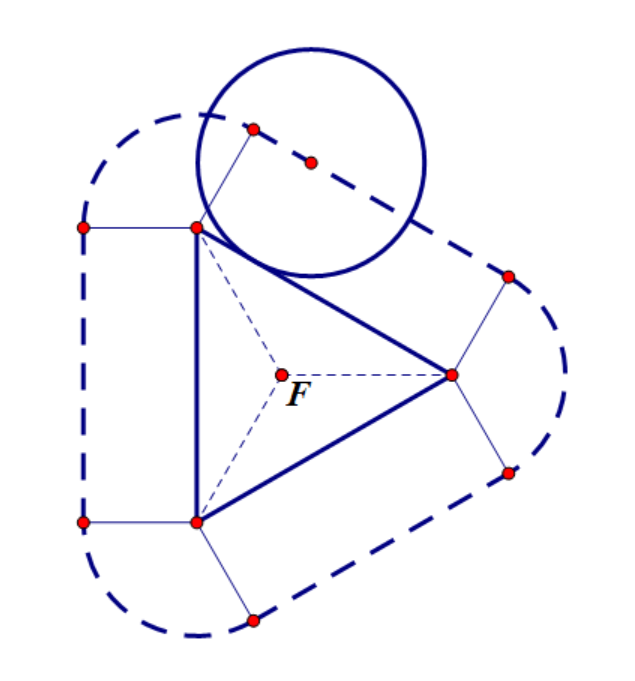
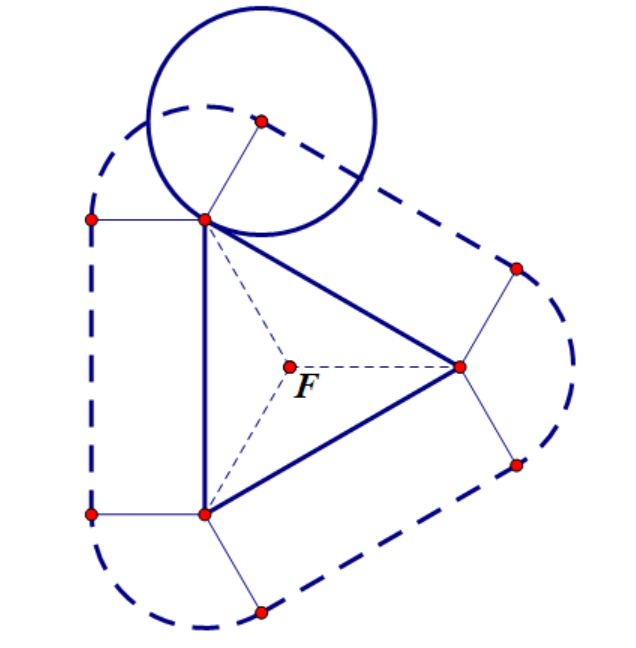
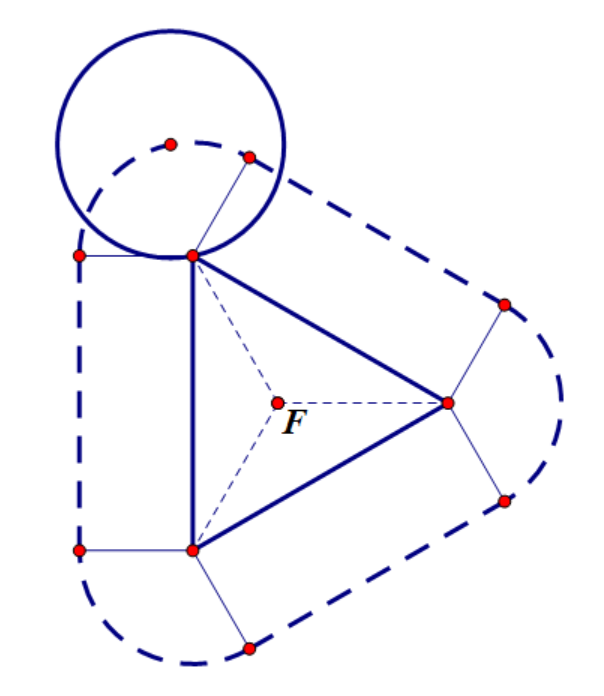
(边接触图示2.10) (分界图示2.11) (角接触图示2.12)
分界条件放大后(图2.13)就是这样
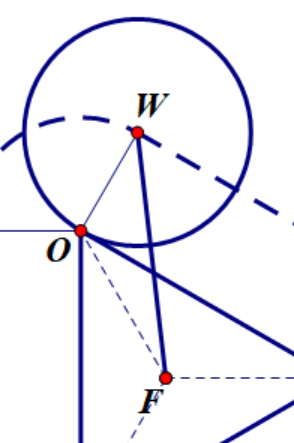
(放大后图示2.13)
计算部分放在计算里
边界接触情况和分界条件了解过后,很容易就能画出边界条件里圆心的轨迹是什么样子,如图(图2.14)
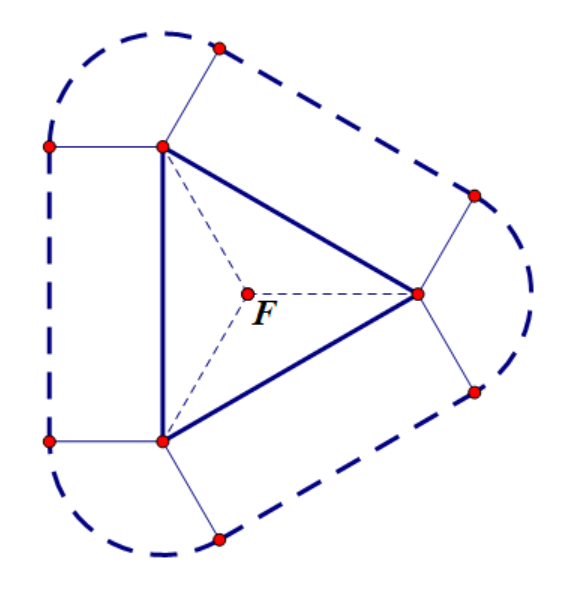
(轨迹图示2.14)
(三)计算
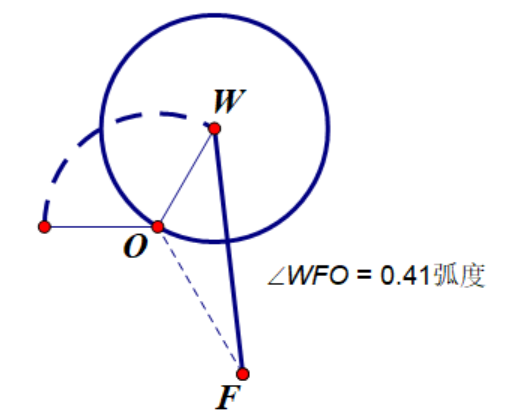
1.分界条件计算
(分界条件放大图示2.15)
WO是圆半径,OF是正多边形的size属性,∠WOF由正多边形的边数量决定,因为是三角形,所以∠WOF=120°,问∠WFO?
方法不少,我用的是两次余弦公式
 (公式2-1)
(公式2-1)
不多赘述,求出cos∠WFO后,反三角函数直接求出∠WFO的弧度β
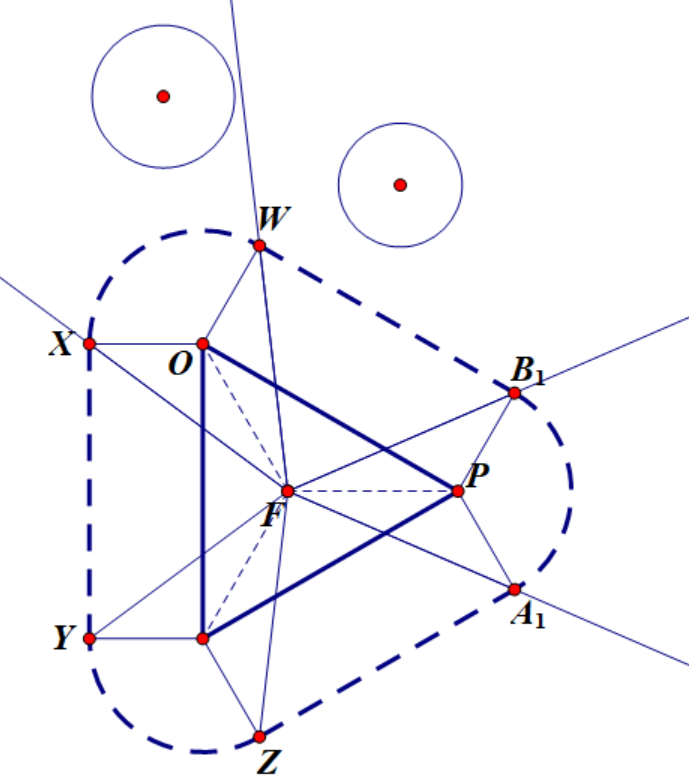
(分界示意图2.16)
如此一来便可以通过圆心和正三角形几何中心连线与X轴产生的夹角α知道,圆和正三角形的距离该用哪种方程约束
例如:-β<α<β时,圆和正三角形应该用角接触的方程约束
2.边接触计算
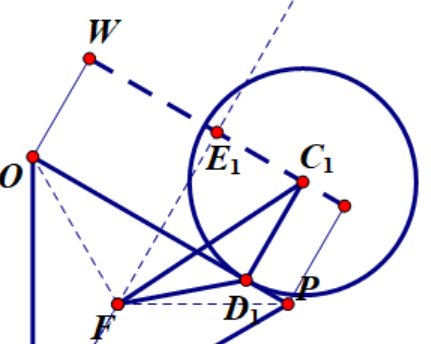
(边接触放大图示2.17)
已知夹角α(即C1F与x轴的夹角),又知∠E1FP为π/3,E1F可以求出来,求出C1F
不多赘述,当C1F大于这个临界距离,就没有接触
3.角接触计算
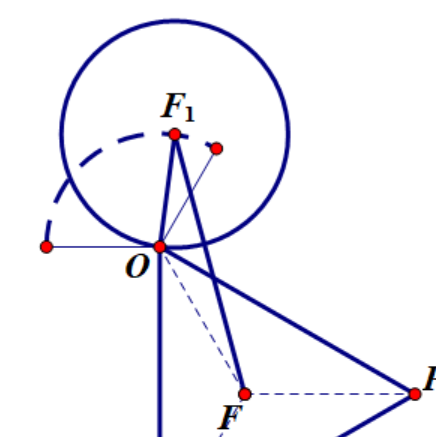
(角接触放大图示2.18)
已知夹角α(即F1F与x轴的夹角),又知∠OFP为2π/3,OF1为圆的半径,OF为this.size,求出FF1
计算过程不多赘述
(四)推广至正n边形,任意偏转角的情况
1.三角形变成正n边形的时候


(正三角形内平分角图示2.18) (正n边形内平分角图示2.19)
∠I1H1J1从∠OFP的2π/3变成了2π/n,∠H1I1J1从∠FOP的π/6变成了(n-2)π/2n
2.偏转角从0变成任意偏转角时


(正三角形偏转0.17图示2.18) (正三角形偏转0.61图示2.18)
(五)代码部分(仅供参考)
1 isCollide(sp){//sp是正多边形,this是圆
2 let deltaY = this.y - sp.y, deltaX = this.x - sp.x, length = Math.sqrt(deltaX * deltaX + deltaY * deltaY)
3 let inter = length != 0 ? Math.acos(deltaX / length) : 0
4 let lengthMin = Math.sqrt(this.size * this.size + sp.size * this.size - 2 * this.size * sp.size * sp.assistAnCos)
5 let cycleAngle = (inter - sp.roundPI) % (2 * sp.divideAngle), cycleCos = Math.cos(cycleAngle - sp.divideAngle)
6 let marginTouchMin = (sp.divideWidth + this.size) / cycleCos
7 let A = Math.acos((sp.size - this.size * sp.assistAnCos) / lengthMin)
8 let angleCount = Math.trunc((inter - sp.roundPI + A) / (2 * sp.divideAngle))
9 let firstAngle = angleCount * (2 * sp.divideAngle) + sp.roundPI
10 let secondAngle = ((inter - firstAngle + A) / A + angleCount * 2 - 1) * sp.divideAngle
11 let angleTouchMin = Math.sqrt(sp.size * sp.size + this.size * this.size + 2 * sp.size * this.size * Math.cos(firstAngle - secondAngle))
12 return length < (cycleAngle > A && cycleAngle < (2 * sp.divideAngle - A) ? marginTouchMin : angleTouchMin) ? true : false
13 }
三. 总结
此次碰撞检测的思考对我的帮助非常大,也加深了我对JavaScript的理解,除此以外,对我自己也是一个鼓舞
也希望,这篇文章可以给看客们一些灵感和帮助,有什么疑惑或者建议也可以加我的QQ:806707508
另外有些东西这篇文章里面并没有讲清楚,后续我会补完
下一篇应该就是动量变化的部分了,我还需要再debug亿会
标签:图示,正多边形,sp,JS,碰撞检测,二维,let,Math,size 来源: https://www.cnblogs.com/redyellowblue/p/13208240.html