拉格朗日插值法入门
作者:互联网
目录
0.什么是插值
在离散数据的基础上补插连续的函数,使得这条连续函数经过所有离散数据点,这个过程就叫插值。
其意义在于:
插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况,估算出函数在其他点处的近似值。
你猜对了,以上均来自百度百科的“插值”词条。
怎么理解这个东西呢?举个例子,操场上有人在踢足球。球员一脚把球踢飞了,假设球始终在一个平面上运行,它的轨迹就可以抽象为一个函数\(f(t)\)(假设它只与与时间相关)。
现在,你借来了一台高速摄像机,拍下了很多张片照片,那么一张照片实际上就是得到了函数图像上的一个点\((t_i,f(t_i))\)。
插值就相当于,你知道了一些照片(离散的数据),想要还原出球的运动轨迹\(f(t)\)。当然,由于你只可能有有限的照片,而函数是连续的,那么你只能去近似地还原函数。这也意味之,插值的结果\(g(t)\)总是无穷多的。
插值有许多方法,包括:三角函数插值;线性插值法;牛顿插值法;拉格朗日插值法......
下面请出今天的主角——拉格朗日...插值法!拍肚皮拍肚皮拍肚皮......
1.拉格朗日插值法
拉格朗日插值法 ( Lagrange Interpolation Polynomial ) 是以十八世纪数学家约瑟夫·拉格朗日 ( Joseph-Louis Lagrange ) 命名的插值法,它可以根据已有离散数据得出多项式的差值结果。
它的思想非常简单,大概可以理解为——硬性配凑!
怎么配凑呢?我们举个例子,平面上有三个点,\((x_1,y_1),(x_2,y_2),(x_3,y_3)(x_1<x_2<x_3)\),我们现在用它们仨插值。
根据小学基础知识,我们知道,这三个点肯定可以唯一确定一个二次函数。
那么我们就尝试找到它,怎么找?拉格朗日想到了一个比较粗暴的方法——咱对于每个点都搞一个子函数\(f_i(x)\),要求\(f_i(x)\)在\(x=x_i\)的时候得到\(1\),在\(x=x_j(j\not=i)\)的时候得到\(0\),把\(n\)个子函数凑起来,得到的函数不就过了\(n\)个点了!
也就是说,我们要计算\(n\)个子函数,第\(i\)个子函数为:
\[f_i(x)= \begin{cases} 1 & x=x_i\\ 0 & x=x_j(j\not=i)\\ I\ don't\ care & otherwise \end{cases} \]
那么插值的结果就是:
\[f(x)=\sum_{i=1}^n y_if_i(x) \]
回到原问题上面来。考虑构造\(f_1(x)\),对于\(f_1(x_j)=0(j>1)\)的情况很好满足,可以想到:
\[f_1(x)=(x-x_2)(x-x_3) \]
怎么让\(f_1(x_1)=1\)呢?我们只需要把不用的丢掉就好:
\[f_1(x)=\frac{(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)} \]
同理构造出\(f_2(x),f_3(x)\),求和得到\(f(x)\):
\[f(x)=\frac{y_1(x-x_2)(x-x_3)}{(x_1-x_2)(x_1-x_3)}+\frac{y_2(x-x_1)(x-x_3)}{(x_2-x_1)(x_2-x_3)}+\frac{y_3(x-x_1)(x-x_2)}{(x_3-x_1)(x_3-x_2)} \]
放几张经典的图片,方便理解:
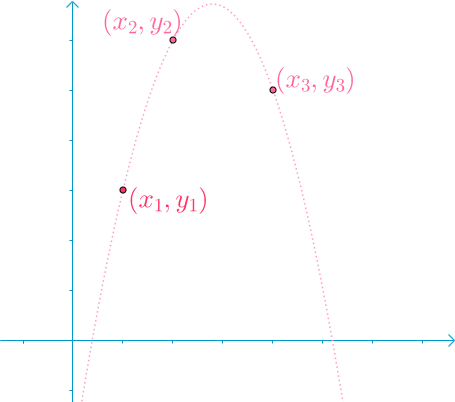
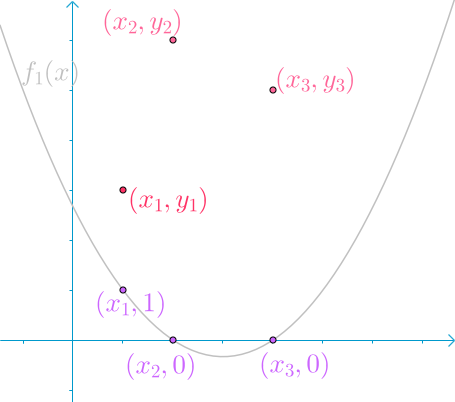
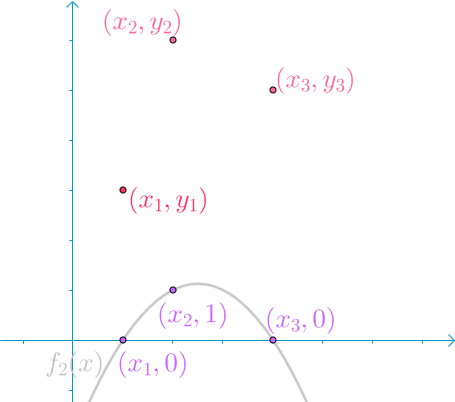
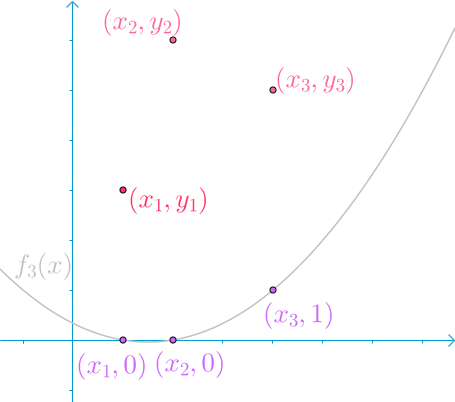
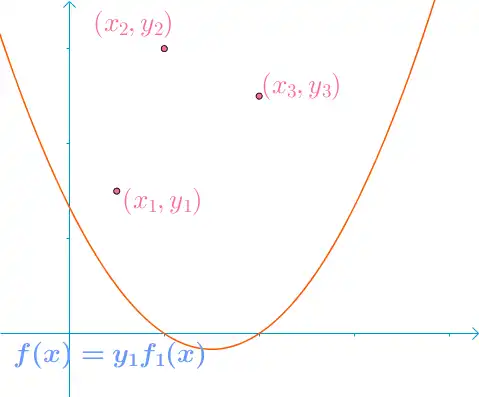
(图源网络,侵联删)
也可以很方便地推广到一般形式:对于\(n\)个点\((x_1,y_1),(x_2,y_2),...,(x_n,y_n)(x_1<x_2<...<x_n)\),设:
\[f_i(x)=\frac{\prod_{j\not=i}(x-x_j)}{\prod_{j\not=i}(x_i-x_j)} \]
那么插值结果就是:
\[f(x)=\sum_{i=1}^ny_if_i(x)=\sum_{i=1}^ny_i\times \frac{\prod_{j\not=i}(x-x_j)}{\prod_{j\not=i}(x_i-x_j)} \]
模板LGP4781:
for( int i = 1 ; i <= N ; i ++ )
{
fi = 1;
for( int j = 1 ; j <= N ; j ++ )
if( i ^ j )
fi = 1ll * fi * fix( k - x[j] ) % mod * inv( fix( x[i] - x[j] ) ) % mod;
ans = ( ans + 1ll * fi * y[i] % mod ) % mod;
}
2.拉格朗日插值法的应用
2.1.多项式插值
拉格朗日插值法可以直接用于离散数据的多项式插值,普通方法的时间复杂度是\(O(n^2)\),经过多项式膜法优化之后可以达到\(O(n\log_2^2n)\)(没错,多项式快速插值就是从拉格朗日插值法优化来的)。
其实,如果不知道拉格朗日插值法,也可以使用一般方法进行多项式插值——直接上待定系数法,用高斯消元解方程组就可以。但是拉格朗日方法显然优点明显:
- 快,快,快得多。高斯消元\(O(n^3)\),拉格朗日只有\(O(n^2)\),还可以优化至\(O(n\log_2^2n)\)。
2.拉格朗日插值法支持取模,而高斯消元法......
3-\(\infty\).还有很多优点,我这里就不一一列举了
不过,在实际应用中,拉格朗日插值法也存在一些缺点。比如说,如果离散数据是变化的,时不时就会多一个点或者少一个点,那么每次变化,拉格朗日插值法都需要重新计算一遍每一个子函数,导致效率非常非常低下。这个时候可以考虑采用易于处理这种情况的牛顿插值法。
再比如,拉格朗日插值法的结果的次数与插值点数成正比。这就意味着,插值点多几个,拉格朗日插值法在非插值点的位置,就会显出与原函数很大的偏差。(具体可以参考龙格现象)
2.2. DP 优化
这两个东西怎么会有关系呢?嗯?
它们确实有关系......
//Editing
标签:拉格朗,frac,入门,插值法,多项式,插值,函数 来源: https://www.cnblogs.com/crashed/p/13124448.html