博客部分公式有格式问题，请前往语雀： https://www.yuque.com/leesamoyed/bvsayi/hrobcr

一、最小二乘法（矩阵表达；几何意义）：

1.线性拟合是用线去拟合样本点：

假设：
其中： ， ，
有：
事实上要拟合的曲线：
其中：（在这里所以我们更倾向于把它写入）

2.最小二乘估计：

最小二乘法定义：
其中： 

得到：

得到：

得到：

所以：

注意：称为伪逆记为

---

第一个几何解释：距离和。
另一个几何解释：对于要拟合的直线我们从另一个角度看：，把想象为维度的一个系数：，横着看就是样本点，竖着看就是一个维，由可以形成一个维空间（一般），形成的向量一般不在维空间（存在噪声之类的），最小二乘法就是在维空间中找到一条线，让距离线（平面最近），那么很显然就是投影。
既然是投影就会垂直于维空间，就会垂直于每一个向量，就有

​
​
​

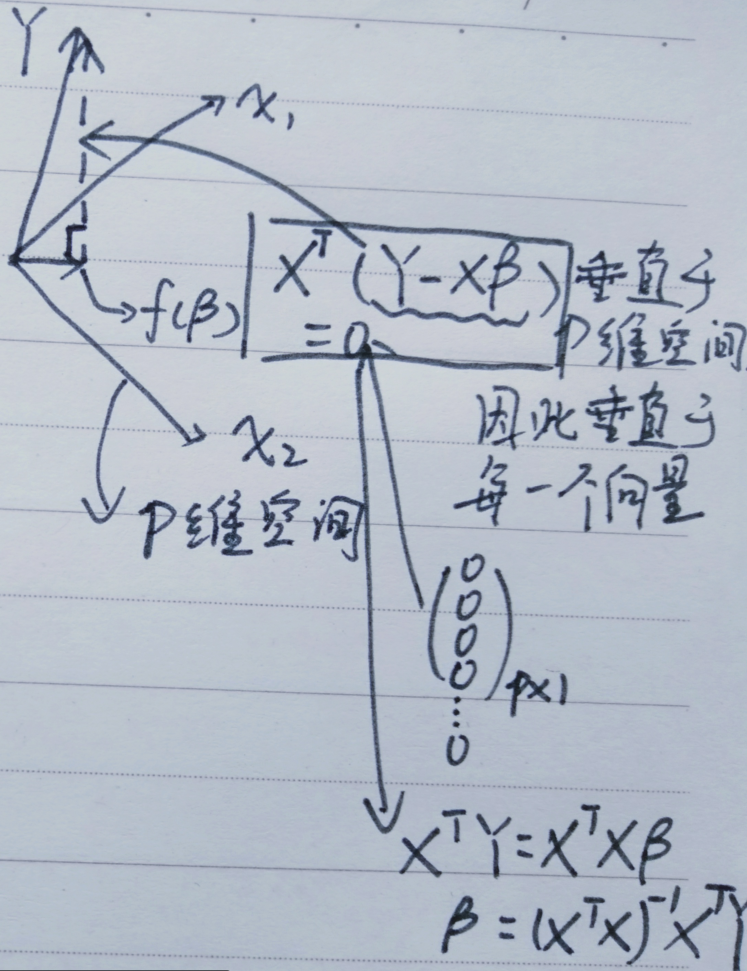
显而易见的是，结果和我们之前推导的结果是一样的，所以从这个角度就很好推证。 
这个就是把误差看成每个维度。

二、最小二乘法-概率角度：

概率视角：
假设：
其中： ， ，
有：
：样本    ：值
最小二乘估计：


 
假设存在噪声：

和最小二乘估计的一样
（noise is Gaussian Dist）

三、正则化-岭回归-频率角度：

Loss Function：    
，个样本，（一般），如果样本纬度高，样本量少容易造成过拟合
过拟合①加数据；②特征选择/特征提取；③正则化；
正则化是对对目标函数的约束
正则化框架：（loss+惩罚）
L1（一范式）Lasso，
L2（二范式）：Ridge（岭回归），（岭回归全称：权值衰减）
L2对应的函数：

四、正则化-岭回归-贝叶斯角度：

频率角度：

贝叶斯角度：
先验：（此时不再是常数）
后验：
    


这里和是我设置的，本质上是超参数，但是这里可以看做常数

这里省略了完全写出来如下：

和一样 

Regularized（noise为Gaussian Dist）（prior也是GD）

线性回归：
①线性    ②全局性    ③数据未加工

标签：维空间,推导,回归,样本,最小,笔记,正则,拟合,线性
来源： https://www.cnblogs.com/leesamoyed/p/12256258.html