数据分析-04概率基础

一：随机事件

　　概率：随机事件发生的可能性的度量

　　范围：0 ~ 1

　

二：排列和组合

　　1.不重复的排列：从n个不同的元素中每次抽取m个不同的元素，按照一定的顺序排成一列，m<n 选排，m = n全排

　　计算公式: P(n,n) = n! , p(m,n) = n(n-1)...(n-m+1) = n!/(n-m)!

　　2.可重复的排列：从n个不同的元素中每次抽取m个可以相同的元素，按照一定的顺序排成一列

　　计算公式：n^m

　　3.组合：从n个不同的元素中每次抽取m个不同的元素，不管顺序成为一组

　　计算公式：C(m,n) = P(m,n)/m! = n!/(m!(n-m)!)

　　4.加法原理和乘法原理

　　加法：完成一件事有不同的方式，完成这件事共有多少种方法

　　乘法：完成一件事需要m个步骤，每个步骤有多少方法，总共有多少种方法

　　

三：概率的定义

　　概率 = 频数/总数

　　大量重复试验条件下，随机事件出现的频率将会随着试验次数的增加而逐渐趋于稳定

　　1.古典概型：　　

　　　　古典概型中，随机事件A发生的概率为：P(a)  = #A / #M

　　　　#A和#M分别代表基本事件个数和总数

　　　　例如：12个球中5个红的，4个白的，3个黑的，从中任取2个球，求没取到红球的概率。

　　　　　　A：取到的两个球没有红球

　　　　　　　　#A = C(2,7) = 21 , #M = C(2,12) = 66

　　　　　　　　P(A) = 21/66 = 7/22

　　2.几何概型：把有限个样本点推广到无限个样本点的场合

　　　　　一般涉及到面积，空间等

 

四：条件概率和贝叶斯公式

　　1.条件概率：在事件B发生的条件下，事件A发生的田条件概率，记为P(A|B)

　　　　P(A|B) = P(AB)/P(B)

　　　　假设A,B是两个随机事件，若P(B) > 0,P(A) > 0则

　　　　P(AB) = P(B)P(A|B)

　　　　P(AB) = P(A)P(B|A)

　　2.全概率公式：

　　　　p(A)=∑n，i=1  p(ABi)=∑ni=1p(A|Bi)p(Bi)

　　3.贝叶斯公式：

　　　　

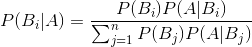
　　详细参考：https://www.cnblogs.com/zhoulujun/p/8893393.html

　　　　

五：独立试验概型

　　随机事件A,B满足P(AB)=P(A)P(B) ，则称为事件A与B相互独立(事件A的发生不受B的影响)

　　A,B为两个事件，P(A)P(B)>0，则A与B独立的充分必要条件是P(A|B)= P(A)或P(B|A)= P(B)

 

六：随机变量

　　1.变异性：随试验结果而变得量

　　2.随机性：出现结果随机，试验前无法预测

　　3.随机变量的每一种取值，就是一个随机事件

　　4.在同一个样本空间可以同时定义多个随机变量

　　　　分为：离散型：取值有限个或可列个

　　　　　　　非离散型------>  

　　离散型随机变量及其分布：设X为离散型随机变量，X的一切可能取值为x1，x2(有限个),x取各个可能值的概率为：Pi = P{X= Xi} = P(Xi)

　　∑oo,k=1(Pk) = 1

　　此部分全部为：概率统计书中的知识，以后用到再补充吧。

　　　　

　　

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

　　　　　

标签：数据分析,概率,04,概型,AB,事件,随机变量,随机
来源： https://www.cnblogs.com/FlowerNotGiveYou/p/11647276.html