显著性水平 p值 z值
作者:互联网
1 显著性水平
显著性水平是估计总体参数落在某一区间内,可能犯错误的概率,用α表示。
α表示原假设为真时,拒绝原假设的概率。
2 P值
在假设检验中常见到P值即概率,反映某一事件发生的可能性大小。
统计学根据显著性检验方法所得到的P 值,一般以P < 0.05 为有统计学差异, P<0.01 为有显著统计学差异,P<0.001为有极其显著的统计学差异。其含义是样本间的差异由抽样误差所致的概率小于0.05 、0.01、0.001。
数据解释
|
P值 |
碰巧的概率 |
对无效假设 |
统计意义 |
|
P>0.05 |
碰巧出现的可能性大于5% |
不能否定无效假设 |
两组差别无显著意义 |
|
P<0.05 |
碰巧出现的可能性小于5% |
可以否定无效假设 |
两组差别有显著意义 |
|
P <0.01 |
碰巧出现的可能性小于1% |
可以否定无效假设 |
两者差别有非常显著意义 |
3 P值和显著性水平区别
显著性水平:显著性水平是假设检验中的一个概念,是指当原假设为正确时人们却把它拒绝了的概率或风险。它是公认的小概率事件的概率值,必须在每一次统计检验之前确定,通常取α=0.05或α=0.01。这表明,当作出接受原假设的决定时,其正确的可能性(概率)为95%或99%。
P值:p值是指在一个概率模型中,统计摘要(如两组样本均值差)与实际观测数据相同,或甚至更大这一事件发生的概率。换言之,是检验假设零假设成立或表现更严重的可能性。p值若与选定显著性水平(0.05或0.01)相比更小,则零假设会被否定而不可接受。
4 z值
z统计是用来衡量样本均值偏离整体均值的方差倍数,就是偏离方差的程度。
根据中心极限定理,总体样本N,每次抽样数n,每次抽样的均值的分布趋近正态分布。也就是随机误差符合正态分布。其分布的数学期望为总体均值μ,方差为总体方差的1/n。
Z值与P值关系 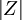 P值 差异程度
P值 差异程度
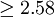 |
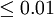 |
非常显著 |
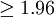 |
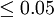 |
显著 |
| <1.96 | >0.05 | 不显著 |
如果检验一个样本平均数( )与一个已知的总体平均数(μ0)的差异是否显著。其Z值计算公式为:
)与一个已知的总体平均数(μ0)的差异是否显著。其Z值计算公式为:
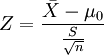
其中:
https://rrsongzi-gmail-com.iteye.com/blog/1860571
标签:显著性,无效假设,假设,水平,显著,概率,0.05 来源: https://blog.csdn.net/genghaihua/article/details/91958522