其他分享
首页 > 其他分享> > ARIMA/Sarima与LSTM的时间序列数据集成学习

ARIMA/Sarima与LSTM的时间序列数据集成学习

作者：互联网

动机

传统时间序列预测中最常使用到的时间序列模型有以下五种，包括：

自回归AR模型以时间序列的前一个值和当前残差来线性地表示时间序列的当前值，而移动平均MA模型则用时间序列的当前值和先前的残差序列来线性地表示时间序列的当前值。

ARMA模型是AR模型和MA模型的组合，其中时间序列的当前值线性地表示为它先前的值以及当前值和先前的残差序列。AR、MA和ARMA模型中定义的时间序列均是平稳过程，即这些模型的均值及其观测值之间的协方差不随时间的变化而变化。

对于非平稳时间序列，必须先将序列转换为平稳的随机序列。ARIMA模型一般适用于基于ARMA模型的非平稳时间序列，其差分过程可有效地将非平稳数据转换为平稳数据。将季节差分与ARIMA模型相结合的SARIMA模型用于具有周期性特征的时间序列数据建模。

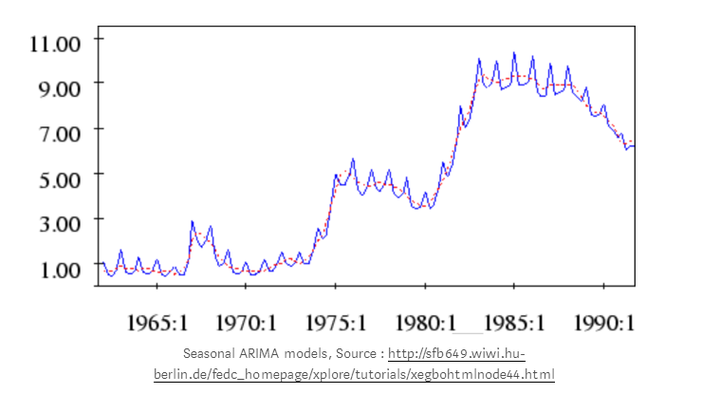
通过比较时间序列中这些算法模型的性能，发现机器学习方法均优于简单的传统方法，其中ETS模型和ARIMA模型的整体性能最好。下图是各模型之间的比较。

 

 

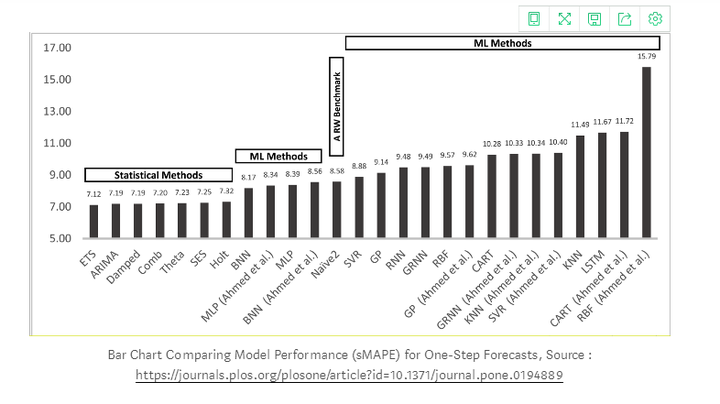
然而，除了传统的时间序列预测外，在时间序列预测的深度学习领域，近年来，递归神经网络(RNN)和长短期记忆(LSTM)在计算机视觉、自然语言处理和金融等多个学科中得到了广泛的应用。深度学习方法在时间序列预测中能够识别诸如非线性度和复杂度等数据的结构和模式。

关于新开发的基于深度学习的预测时间序列数据的算法，如“长短期记忆 (LSTM)”，是否优于传统的算法， 仍然是一个开放的函待研究的问题。

 

本博的结构如下：

·了解使用SARIMA进行时间序列建模时，如何与其他基于空间、基于决策和基于事件的模型进行集成学习。

然而，本文没有对更为复杂的时间序列问题做深入的阐述，例如：复杂的不规则时间结构，缺失的观测，强噪声和多变量之间复杂的相互关系的数据集等等。

LSTM

LSTM是一种特殊的RNN，它由一组具有特征的单元集合组成，利用这些特征来记忆数据序列，集合中的单元用于捕获并存储数据流。此外，集合中的单元构成先前的模块与当前的模块的内部互连，从而将来自多个过去时间瞬间的信息传送给当前的模块。每个单元中会使用到门，为下一个单元处理、过滤或添加单元中的数据。

单元中的门基于Sigmoidal神经网络层，使单元可以选择性地让数据通过或丢弃，每个sigmoid层输出一个在0到 1之间的数字，这个数字为每个单元中应该通过的数据的数量。更准确地说，如果这个值为0，意味着“不让任何数据通过”， 如果这个值为1，则表示“让所有数据都通过”。为了控制每个单元的状态，每个LSTM涉及三种类型的门：

遗忘门输出一个介于0到1之间的数字，其中1表示“完全保留此值”；而0则意味着“完全忽略此值”。

记忆门决定选择哪些数据通过sigmoid层和tanh层后需要存储到数据单元中。初始sigmoid层，称为“输入门层”，决定需要对哪些数值进行修改，随后，由tanh层生成可以添加到状态的新候选值的向量。

输出门决定每个单元输出的内容，根据数据过滤及新增数据后数据单元的状态，输出门会输出一个数据值。

在工作原理和实现机制两方面，LSTM -模型提供了比ARIMA

更多的微调选项。

LSTM在时间序列预测中的应用

研究发现，使用特定数据集训练的单个LSTM网络很可能在其它完全不同的时间序列上表现不佳，为此，需要执行严格的参数优化。由于LSTM在预测领域非常成功，研究人员采用了一种所谓的堆叠集成方法，将多个LSTM网络进行叠加和组合，以提供更精确的预测，旨在为预测问题提供一个更广义的模型。

通过对四种不同的预测问题进行研究，依据RMSE评价尺度， 得出了堆叠LSTM网络的性能优于常规LSTM网络和ARIMA模型的结论。

通过调整每个LSTM的参数，可以提高集成方法的总体质量。单个LSTM网络性能之所以性能差的原因是需要对大量LSTM网络参数进行调整。因此，集成LSTM网络的概念得以发展，它减少了大量优化参数的需要，并提高了预测的质量，从而为预测问题提供了更好的选择。

 

 

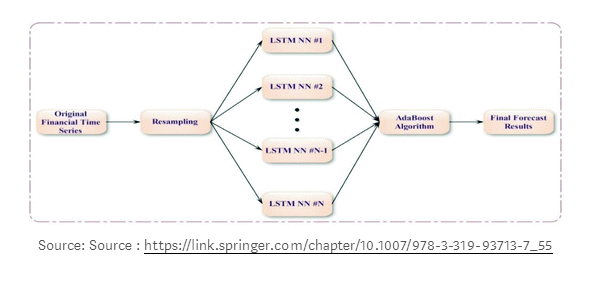
在其他集成技术中，如上图所示，具有长期短期记忆(LSTM)的混合集成学习可以用来预测金融时间序列。AdaBoost算法用于对来自多个独立的长期短期记忆(LSTM)网络进行组合预测。

首先，利用AdaBoost算法对数据进行训练，从原始数据集中生成替换样本，得到训练数据；然后，利用LSTM分别对每个训练样本进行预测；最后，采用AdaBoost算法对所有LSTM预测器的预测结果进行综合，生成集成结果。对两个主要的日汇率数据集和两个股票市场指数数据集的实证结果表明，AdaBoost-LSTM集成学习方法优于其他单一预测模型和集成学习方法。

AdaBoost-LSTM集成学习方法在金融时间序列数据预测中有着广阔的应用前景，对于汇率和股票指数等非线性和不规则的时间序列数据也有很好的应用前景。

 

 

 

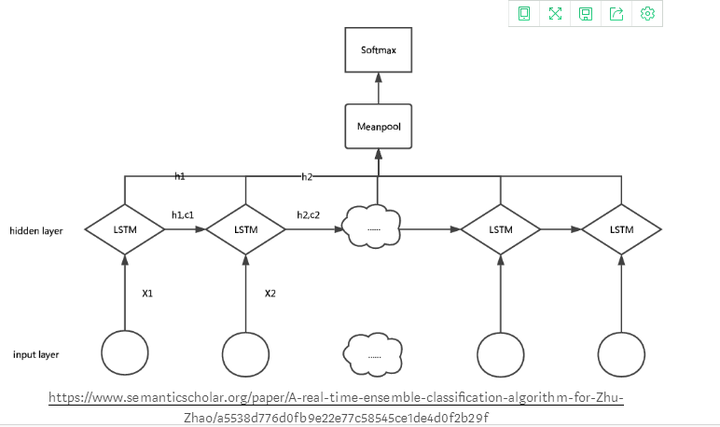
如上图所示，在LSTM中进行集成学习的另一个例子是，当输入层包含从时间 t1 到tn的输入时，每个时间瞬间的输入被输入到LSTM层，每个LSTM层HK的输出代表时间k的部分信息，被输入到输出层，输出层从接收到的所有输出中聚合和计算出均值。此外，将均值输入Logistic回归层以预测样本的标签。

ARIMA

ARIMA算法为捕捉时间序列数据中时间结构的一类模型，然而，单独用ARIMA模型却很难对变量之间的非线性关系进行建模。

差分自回归移动平均模型(ARIMA) 是一种将自回归(AR)过程和移动平均(MA)过程相结合的广义自回归移动平均(ARMA)模型，它为时间序列建立一个复合模型。

AR：自回归。一种使用一个观察和多个滞后观测之间的依赖关系的回归模型。

I：差分。通过计算不同时间观测值的差值，使时间序列平稳化。

MA：移动平均。当对滞后观测(q)使用移动平均模型时，计算观测值与残差项之间的依赖性的一种方法(Q)。阶为p的AR模型的一种简单形式，即AR(P)，可以写成一个线性过程，由以下公式表达：

 

 

 

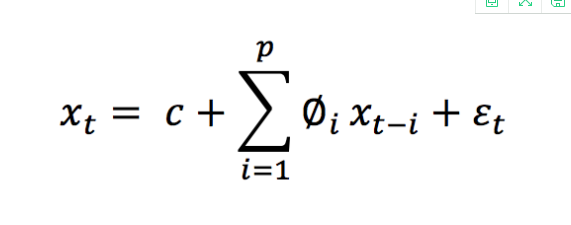
这里，xt表示平稳变量，c是常数，∅t中的项是滞后1，2，…的自相关系数。残差p和ξt是均值为零、方差为 σt²的高斯白噪声序列。

ARIMA模型的一般形式表示为ARIMA(p，q，d)。对于季节性时间序列数据，短期非季节性成分很可能对模型有贡献。ARIMA模型通常表示为ARIMA(p，q，d)，其中：-

 

 

例如，ARIMA(5，1，0)表示自回归的滞后值设置为5，它使用1阶差分使时间序列平稳，不考虑任何移动平均窗口(即窗口的大小为零)。RMSE可以作为一个误差度量指标来评价模型的性能，评估预测的准确性，并对预测的准确性做出评价。

为此，需要用到季节性ARIMA模型，它是一个包含了非季节性和季节性因素的复合模型。将季节性ARIMA模型的一般形式表示为(p, q, d) X (P, Q, D)S，其中p是非季节性AR阶数，d是非季节性差分，q是非季节性MA阶数，P是季节性AR阶数，D是季节性差分，Q是季节性MA阶数，S是重复季节模式的时间跨度。预估季节性ARIMA模型的最重要步骤是识别(p，q，d)和(P，Q，D)的值。

根据数据的时间图，如果方差随时间增长，则应采用方差平稳化变换和差分法。

利用自相关函数(ACF)来计算由p个滞后隔离的时间序列中观测值之间的线性相关，利用偏自相关函数(PACF)来确定需要多少个自回归项q，利用逆自相关函数(IACF)来检测过差分，之后可以得到自回归阶p、差分阶数d的初值，移动平均阶q及其对应的季节性参数P、D和Q。参数d是从非平稳时间序列到平稳时间序列的差分频度变化的阶数。

在对单个时间序列数据采用“自回归移动平均(ARMA)”的单变量方法过程中，将自回归(AR)模型和移动平均模型(MA)相结合，单变量“差分自回归移动平均模型(ARIMA)”是一种特殊的ARMA模型，在这个模型中考虑了差分。

多元ARIMA模型和向量自回归模型(VAR)是另外两种流行的预测模型，它们通过考虑多个演化变量来推广一元ARIMA模型和单变量自回归(AR)模型。

ARIMA是一种基于线性回归的预测方法，最适合于单步样本预测。在这里，所提到的算法为多步样本预测与重新估计，即每次模型被重新拟合，以建立最佳的估计模型。该算法以输入“时间序列”数据集为基础，建立预测模型，并计算预测的均方误差。它存储两个数据结构来保存每次迭代时累积添加的训练数据集，即：“历史”值和对测试数据集的连续预测的 “预测”值。

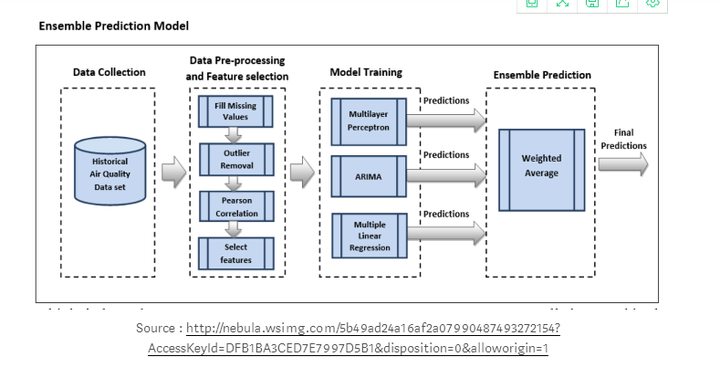
基于ARIMA的集成学习

对ARIMA、多层感知器(MLP)和多元线性回归(MLR)三种预测模型分别进行训练、验证和测试，得到目标污染物浓度预测。为了训练和拟合ARIMA模型，利用自相关函数(ACF)和偏自相关函数(PACF)对p、d、q值进行了估计。MLP模型采用以下参数来建立：用于权重优化的求解器是lbfgs，因为它能够更快地收敛，并且对于较少维数的数据性能更为优越。

与随机梯度下降优化器相比，它得到了更优的结果，它采用激活函数“relu”表示修正线性单元(RELU)函数，从而避免了梯度消失的问题。然后利用加权平均集成技术将每个模型的预测合并为最终预测。加权平均集合是将每个模型的预测与权重相乘，然后计算出其平均值。可以根据各模型的性能，调整各基本模型的权重。

每个模型的预测采用加权平均技术进行组合，其中各个模型根据其性能被赋予不同的权重，对性能较好的模型给予更高的权重，权重的分配原则应确保权重之和必须等于1。

SARIMA

ARIMA是目前应用最广泛的单变量时间序列数据预测方法之一，但它不支持具有季节性成分的时间序列。为了支持序列的季节分量，将 ARIMA模型扩展成为SARIMA。SARIMA (季节性差分自回归移动平均模型应用于包含趋势和季节性的单变量数据，SARIMA由趋势和季节要素组成的序列构成。

与ARIMA模型相同的一些参数有：

不属于ARIMA的四个季节性因素有：

SARIMA模型可以定义为：

SARIMA (p, d, q) (P,D,Q) m

如果m为12，则它指定每年的季节周期为月数据。

SARIMA时间序列模型也可以与基于空间和事件的模型相结合，以生成解决多维ML问题的集成模型。这样的ML模型可以用来预测一年中不同时刻的蜂窝网络中的小区负荷,如下面的样本图所示。

时间序列分析中的自相关、趋势和季节性(工作日、周末效应)可以用来解释时间影响。

区域和小区的负荷分布可以用来预测不同的时间间隔内的稀疏和过载的单元。

利用决策树来预测事件(假日、特殊的群众性集会和其他活动)。

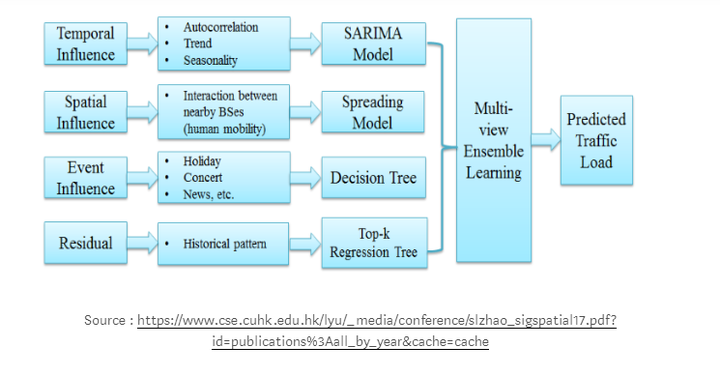
数据集、问题和模型的选择

在分析经典机器学习和深度学习机制需要解决的问题时，在最终选择正确的模型之前，需要考虑以下因素。

经典时间序列模型(ARIMA/SARIMA)和深度学习模型性能指标的不同。

首先，数据是高度动态的，通常很难梳理出时间序列数据内嵌的结构；其次，时间序列数据可以是非线性的，并且包含高度复杂的自相关结构。不同时间周期的数据点可以相互关联，并且线性近似，有时不能对数据中的所有结构建模。诸如自回归模型之类的传统方法试图估计出模型的参数，该模型可视为对生成数据的结构的平滑近似。

综上所述，ARIMA用来对线性关系的数据更好地建模，而RNN(取决于激活函数)则更好地建立了具有非线性关系的模型数据。ARIMA模型为数据科学家提供了一个更优的选择，之后，当数据通过 Lee，White和Granger(LWG)检验之后的残差中仍然包含非线性关系时，可以用RNN这样的非线性模型对数据集进一步处理。

在对一组财务数据分别应用LSTM和ARIMA之后，结果表明LSTM优于ARIMA， LSTM算法与ARIMA相比，预测准确率平均提高到了85%。

结论

本文最后给出了一些案例研究，为什么特定的机器学习方法在实践中表现得不尽如人意，但是它们在人工智能的其他领域中的表现却非常出色？为此，本文对ARIMA/SARIMA和LSTM模型性能不佳的原因进行了评价，设计出了提高模型性能和精度的机制。这些模型的应用领域及其性能如下：

参考文献：

  1. https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0194889
  2. https://machinelearningmastery.com/findings-comparing-classical-and-machine-learning-methods-for-time-series-forecasting/
  3. https://arxiv.org/pdf/1803.06386.pdf
  4. https://pdfs.semanticscholar.org/e58c/7343ea25d05f6d859d66d6bb7fb91ecf9c2f.pdf
  5. 《用于稳健时间序列预测的集成递归神经网络》，作者：S.Krstanovic和H.Paulheim，载于“人工智能”34 期、编辑：M.Bramer和M.Petridis，斯普林格国际出版社，2017，pp.34-46，ISBN：978-3-319-71078-5。
  6. https://link.springer.com/chapter/10.1007/978-3-319-93713-7_55
  7. http://nebula.wsimg.com/5b49ad24a16af2a07990487493272154?AccessKeyId=DFB1BA3CED7E7997D5B1&disposition=0&alloworigin=1
  8. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC3641111/
  9. 基于节能蜂窝网络的流量预测：一种机器学习方法 Method https://www.cse.cuhk.edu.hk/lyu/_media/conference/slzhao_sigspatial17.pdf?id=publications%3Aall_by_year&cache=cache

文章来源：https://zhuanlan.zhihu.com/p/67092940

标签：预测,模型,ARIMA,Sarima,序列,LSTM,数据
来源： https://blog.csdn.net/Poo_Chai/article/details/90924860