Word Embeddings And Word Sense

最近在学习2019版的CS224N，把所听到的知识做成笔记，以便自己不时地回顾这些知识，另外还希望可以方便没有时间看课程的朋友们用来做个快速的overview（当然，亲自上课是最好的选择）。我也尽量地把所有课程的知识细节都写出来，以及一些相关的知识都牵扯进来。

---

近年来NLP领域发展变化得比较大，语言模型已经开始大行其道，词嵌入技术差不多变成了只是一个稀疏向量的稠密化过程。尽管如此，我认为词嵌入技术仍然还是NLP发展历程中重要的里程碑，因为这个技术让人们可以用数字来描述词义，并且在很多领域都取得了比之前更好的表现。

Discrete Representation

文本是非结构化数据，该如何表达以适合用于分析是一个比较有挑战的问题。One-Hot编码是解决这个问题的最简单也是最直接的办法。
接下来用一段话简单描述一下One-Hot编码。假设我们词表(vocabulary)有V个单词，我们对每个单词都赋予一个下标i（i属于0…V-1），每个单词由一个长度为V的向量表示，其中只有对应下标的元素为1，其他元素均为0。借用Tensorflow官方的一个图：

 图一 One-Hot编码示例(来自https://tensorflow.google.cn/guide/feature_columns)

One-Hot编码虽然简单易用，但是缺点也很明显：

1. 词向量长度等于词表长度，而且词向量是及其稀疏的，当词表很大时计算复杂度会很大;
2. 任意两个词都是正交的，意味着无法从One-Hot编码中获取词与词之间的关系
3. 任意两个词的距离都是相等的，无法从距离上反应两个词的语义相关度

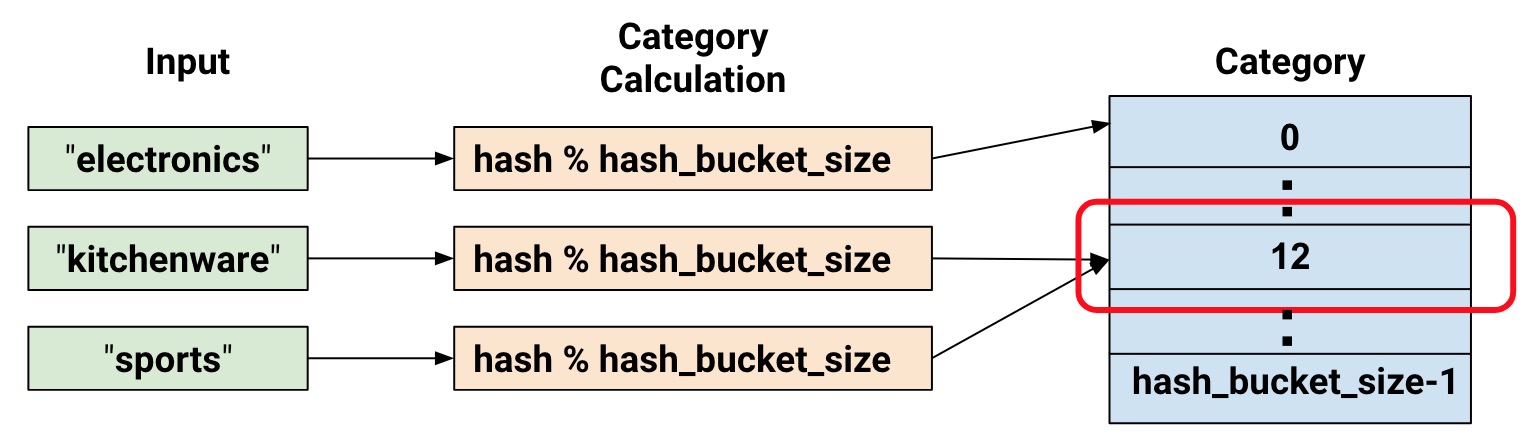顺带一提，针对缺点1,其实早期已经有一些解决办法，其中比较简单的办法是Hash Trick。Hash Trick是将每个词通过一个哈希函数计算得出各自的哈希值，然后让哈希值作为这个词在词表中的index。这么一顿操作的结果是，词向量变成了一个可人为指定长度的向量，极大地降低了稀疏性带来的额外计算。另外这种方法也面临着哈希冲突的问题（即不止一个词映射到同一个哈希值）。不管怎样，这种方法很直接，很暴力，但也被实践证实了是很有效的。不过这个trick仍然无法给词义计算带来帮助。

 图二 Hash Trick(来自https://tensorflow.google.cn/guide/feature_columns)

Distributional Representation

说实话其实我一直理解不了Distributional这个词（可能是有什么渊源？或者是相对于只有一个非零元素的离散性词向量而言？欢迎各位大神指教），我的理解就是分布式表述是用连续性的稠密向量来表示词语。分布式表述的好处在于它能更好地表达词的意思，而且通过稠密向量也可以很容易的计算出词与词的关系（词与词之间不再两两正交），而且有新词语来的时候我们不需要扩展向量的维度，只需要将词语映射到维度远小于词表长度的向量就好了。

顺带提一下，后续的很多方法都是基于这句富含哲学意义的话：

You shall know a word by the company it keeps.

人们明白了一个指导思想：语义是由上下文赋予的，于是，人们开始利用上下文来计算词的语义。

Word2Vec

Word2Vec是谷歌研究员在2013年提出来的方法，我觉得它是里程碑式的诞生，因为它不仅仅可以用于捕获词义，还可以用来辅助解决其他NLP领域的问题。接下来，我先介绍它大概的算法原理，具体实现细节会放到后面（按课程顺序）。
这里归纳一下：

1. Word2Vec需要用大量的语料来实现自监督学习(self-supervise learning)。其中，语料是NLP中对用来训练的文本数据的称呼，自监督学习是指训练方法是监督学习，只是这个label是来自于自身（回顾一下那句富含哲学意义的名言）。
2. 在计算时采用固定大小的采样窗口，使用中间词c(center word)去预测环境词o(context words)（图三），或者反过来使用环境词预测中间词。在遍历语料的过程中，下文我们默认采用中间词预测环境词这种方法，即P(o|c)。

 图三 中间词预测上下文(来自https://www.jianshu.com/p/af8f20fe7dd3) 3. 使用中间词预测环境词，即在输入中间词的时候需要使对应环境词的预测概率尽可能的大，即要最大化`P(o|c)`，而预测函数则定义为： $$P(o|c) = \dfrac{exp(u_o^{\prime}\cdot{v_c})}{\sum_w{exp(u_w^{\prime}\cdot{v_c})}}$$ 4. 模型参数即为词向量（注：在上例中每个模型中都有两个向量：u和v）。 5. 求偏导（以对v为例）： $$ \begin{align} \frac{\partial}{\partial{v_c}}{logP(o|c;\theta)} &=\frac{\partial}{\partial{v_c}}{log[exp(u_o^{T}\cdot{v_c})]}-\frac{\partial}{\partial{v_c}}{log[\sum_w{exp(u_w^{T}\cdot{v_c})}]}\\ &=u_o-\sum_x^{|V|}{\frac{{exp(u_x^{T}\cdot{v_c})}}{\sum_wexp(u_w^{T}\cdot{v_c})}\cdot{u_x}}\\ &=u_o-\sum_x^{|V|}{P(x|c)}\cdot{u_x} \end{align} $$

为什么每个词要有两个词向量呢？课程里面说那是为了方便数学展示以及更容易优化，实际上可以只用一个向量，如果用两个向量来表示的话，最终可以取平均的方式得到最终词向量。

接下来谈谈最经典的两个词嵌入模型CBOW和Skip-Gram，另外还有一个trick Negative Sampling。

CBOW

CBOW（Continuous Bag-of-Words）是由环境词来预测中间词的模型，预测函数为P(c|o)。

Skip-Gram

与CBOW相反，Skip-Gram是由中间词预测环境词的模型，预测函数为P(o|c)。

 图四 CBOW和Skip-Gram(来自https://www.jianshu.com/p/d534570272a6) 注意：图中左边网络隐藏层的聚合操作一般是average操作。

Negative Sampling

在词嵌入模型中，隐藏层到输出层的映射是用softmax来计算概率的，然后再通过这个概率找到最大值（归纳中的第三点）。但这个过程中相当于每个词都要计算一次softmax概率，而且并且在backprop的时候所有词向量都会被更新，我们希望采取一些方法去避免这么大量的计算发生，所以后来的提出了Negative Sampling这个trick来做改进。
Negative Sampling把多分类问题转化成了二分类问题，这里以Skip-Gram为例，预测函数改为：
$P(o|c) = \begin{cases} 1, & \text{if o is context words} \\ 0, & \text{if o is random words} \end{cases}$P(o∣c)={1,0,​if o is context wordsif o is random words​

可以理解为，Negative Sampling是把“中间词的周围最可能是哪些词”这个问题转化成“中间词周围是这些词有多大可能”。

这里稍微备注一下,这里等号其实是不成立的，只是为了方便理解，由中间词预测出来对应上下文环境词概率应该尽量靠近1，而预测出随机抽取的负样本的概率应该尽量靠近0

这样目标函数改成为
$J(\theta) = \frac{1}{T}\sum_{t=1}^{T}J_{t}(\theta)$J(θ)=T1​t=1∑T​Jt​(θ)

其中
$J_{t}(\theta) = log\sigma(u_o^{T}\cdot{v_c}) + \sum_{i=1}^{k}E_{j\sim{p(w)}}{[log{\sigma{(-u_j^{T}\cdot{v_c})}}]}$Jt​(θ)=logσ(uoT​⋅vc​)+i=1∑k​Ej∼p(w)​[logσ(−ujT​⋅vc​)]

k表示负样本（随机词）个数，$$\sigma$σ$表示sigmoid函数。

在上式中，加号左边部分表示由中间词预测出环境词的概率，这个概率应尽可能的大。而加号右边表示预测出不是负样本的概率的加权平均数（注意有个负号），这个项也应该尽可能的大。所以上式是个最大化的目标，当然我们更习惯写成最小化目标，这只需要取相反数就可以了。
最后一个点是这个负采样应该按照一个什么样的原则来进行，也就是上式中的$$P(w)$P(w)$怎么决定的问题。显然我们采用完全随机抽样的话是不科学的，因为通常高频词的作用要大一点，我们需要稍微倾向高频词一点。但是如果直接按照词频来采样的话，低频词被抽取的概率就非常的低，所以需要采用一些措施来实现倾向高频词的同时可以也均衡低频词的被抽取概率。

这个概率的一般计算方法是
$P(w) = \frac{U(w_i)^{\frac{3}{4}}}{\sum_{j=0}^{|V|}{U(w_j)^{\frac{3}{4}}}}$P(w)=∑j=0∣V∣​U(wj​)43​U(wi​)43​​

上式中U表示Uni-Gram，即一元模型分布，也就是词频的统计。

除Negative Sampling之外还有一个trick叫Hierarchy Softmax，Hierarchy Softmax多用在CBOW,Negative Sampling多用在Skip-Gram。
Hierarchy Softmax同样是用二分类代替了多分类，但关键在于这个trick需要把每个词根据词频构建成哈夫曼数，每个词都变成了0-1的编码串。在CBOW输出的时候，根据词编码串的长度来决定要做多少次的二分类，但除根节点外每一次的二分类使用的权值都要根据上一次输出的编码结果来决定。因为哈夫曼树是前缀树，即任何一个编码都不可能是另一个编码的前缀，所以输出结果的时候只需要探索到叶节点即可对应到具体的词。
使用Hierarchy Softmax平均的探索深度为log2(V)，相对所有V个词都计算还是要节省不少的计算量。

Count Based Method

深度学习大行其道之前，NLP很多工作都是基于统计来进行的。
最简单的做法是把我们能获取的语料做成一个文档-词矩阵或者词-词矩阵，例如：

 图五 词-词共现矩阵(来自https://www.cnblogs.com/DjangoBlog/p/6421536.html)

我们可以用行与行之间的距离来计算出词与词之间的关系如何。当然，这样的矩阵很稀疏，我们可能需要用更短的向量来做更高效的计算，这时候可以考虑使用SVD对这样一个贡献矩阵进行分解

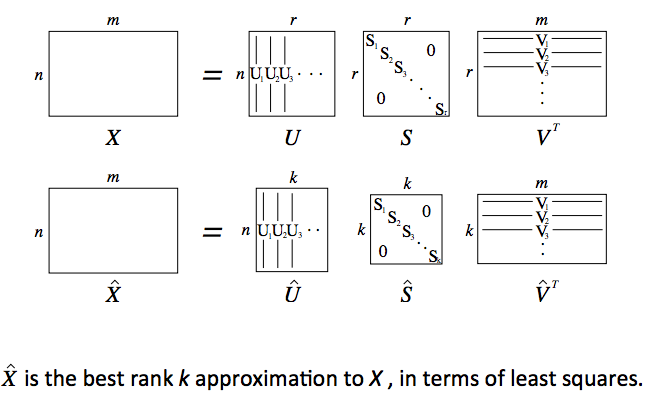 图六 SVD分解示例(来自https://www.cnblogs.com/DjangoBlog/p/6421536.html)

我们只需要用分解出来的隐语义向量进行计算，同时这样的隐语义向量还可以忽略一些噪音的影响（把较小的奇异值干掉），这样的方法有个看起来高大上的名字叫LSA（latent sementic analysis）。

相对于CBOW、Skip-Gram之类的新方法，LSA之类的传统方法有一些更优之处:

1. 训练更快速
2. 高效利用统计属性

但也有一些缺点：

1. 只适合用于捕获词义
2. 构建词-词共现矩阵需要大量的内存

GloVe

网上似乎详细写GloVe的博文不多，然后又因为现在正儿八经使用词嵌入模型去先把词向量训练一遍的情况已经不多了，我其实只是大致看了一下原论文，课程也没怎么说这个地方，所以下面内容部分主要是对论文原文推导部分的翻译，另外也有部分来自其他博文。

GloVe最基本的观点是共现概率比可以更好的捕捉到词义。

先介绍一些符号：

• $$X_{ij}$Xij​$ 表示词j在词i的上下文次数
  
• $$X_i = \sum_{j}{X_{ij}}$Xi​=j∑​Xij​$ 即表示所有词出现在词i上下文的总次数
• $$P_{ij} = P(j|i) = {X_{ij}}/{X_{i}}$Pij​=P(j∣i)=Xij​/Xi​$ 表示词j在词i上下文的概率

然后引入一个栗子：
例如说我们现在要比较两个词，词i为ice（冰），词j为steam（蒸汽）。

 图七 共现概率比(来自https://zhuanlan.zhihu.com/p/33138329)

图中的数值是由斯坦福的语料计算得到的。常识告诉我们，solid（固体）应该更靠近ice的属性，而gas（气体）应该更靠近steam，water（水）是两者公共属性。但直接从共现概率来看的话，这个关系并不十分明显，但如果我们两者相比就很明显的发现，数值越大则相对关系越强，数值越小则相对关系越弱，数值越靠近1，则该属性上的同等程度越接近。这个现象也很符合逻辑。

通常我们传统的学习共现概率比的方式是直接从语料库计算得到的：
$F(w_i,w_j,\tilde{w}) = \frac{P_{ik}}{P_{jk}}$F(wi​,wj​,w~)=Pjk​Pik​​
其中$$w_i \in R^d$wi​∈Rd$是词向量，$是词向量，$\tilde{w}\in R^d$w~∈Rd$是上下文词向量。F是词向量函数。

因为我们的目的是基于共现概率比来捕捉词义，而词向量又是线性结构的，所以我们可以把这个函数F修改为
$F(w_i-w_j,\tilde{w}) = \frac{P_{ik}}{P_{jk}}$F(wi​−wj​,w~)=Pjk​Pik​​

上式中函数F的参数是两个向量，但输出结果是单值，而F可用复杂的模型来实现，例如神经网络。这样的映射关系可能会影响我们想要捕捉的线性关系（doing so would obfuscate the linear structure we are trying to capture），因此改为向量内积：
$F(({w_i}-{w_j})^{T}\cdot{\tilde{w}_k}) = \frac{P_{ik}}{P_{jk}}$F((wi​−wj​)T⋅w~k​)=Pjk​Pik​​

在词-词共现矩阵中，词$$w_i$wi​$跟上下文词$跟上下文词$\tilde{w}_k$w~k​$的区别并不大，也就是说，它们的位置其实完全是可以调过来的。为了保持模型的对称性，我们需要F是同态的（homomorphism）：
$F(({w_i}-{w_j})^{T}\cdot{\tilde{w}_k}) = \frac{F(w_{i}^{T}\tilde{w}_k)}{F(w_{j}^{T}\tilde{w}_k)}$F((wi​−wj​)T⋅w~k​)=F(wjT​w~k​)F(wiT​w~k​)​

由上面的式子我们已经有
$F(w_{i}^{T}{\tilde{w}_k}) = P_{ik} = \frac{X_{ik}}{X_{i}}$F(wiT​w~k​)=Pik​=Xi​Xik​​

如果F为exp，再取log，那么可以得到
$w_{i}^{T}\tilde{w}_{k} = log(P_{ik}) = log(X_{ik}) - log(X_{i})$wiT​w~k​=log(Pik​)=log(Xik​)−log(Xi​)

因为$$log(X_{i})$log(Xi​)$跟`k`无关，所以把它变成一个$跟‘k‘无关，所以把它变成一个$w_i$wi​$的偏置值$的偏置值$b_i$bi​$，最后为了保持对称性，给$，最后为了保持对称性，给$\tilde{w}_{k}$w~k​$也加上一个偏置值$也加上一个偏置值$\tilde{b}_{k}$b~k​$得到
$w_{i}^{T}\tilde{w}_{k} + b_i + \tilde{b}_{k} = log(X_{ik})$wiT​w~k​+bi​+b~k​=log(Xik​)

到这里就已经可以得到一个关系了：共现矩阵中词i与k的共现次数的对数等于这两个词的词向量内积再加上各自的偏置值。
这里有两个问题：

• 词-词共现矩阵是十分稀疏的，也就是矩阵中很多元素都为0，需要采取一定办法避免$$log0$log0$的情况
• 这样的模型的主要缺陷是对所有的共现值是平等处理的，需要添加一个权值函数$$f(x)$f(x)$

把损失函数构造成最小二乘损失，那么就变成了一个最小二乘回归问题了
$J = \sum_{i,j=1}^{V}{f(x_{ij})(w_{i}^{T}\tilde{w}_{j}+b_i+\tilde{b}_j-logX_{ij})^2}$J=i,j=1∑V​f(xij​)(wiT​w~j​+bi​+b~j​−logXij​)2

其中，$$f(x)$f(x)$的性质

1. $$f(0)=0$f(0)=0$；
2. 必须是非递减函数，使低频共现不能有大的权重；
3. 削弱高频共现的影响，使高频共现不会过高权重。

论文中取的权值函数为
$f(x) = \begin{cases} {(x/x_{max})^\alpha}, &amp; x &lt; x_{max} \\ 1, &amp; \text{otherwise} \end{cases}$f(x)={(x/xmax​)α,1,​x<xmax​otherwise​

图像如下

 图八 权值函数f取α=3/4(来自https://zhuanlan.zhihu.com/p/33138329)

评估

任何模型都要经过评估，课程介绍的两个评估方式：内在评估（intrins）和外在评估（extrinsic）。

内在评估意思是在训练好的词向量中评估，例如做类比。类比又可以分为语义类比和语法类比，语义类比就例如像king-man::queen-woman，而语法类比就类似于big-bigger::fast-faster。通过类比计算准确率即可以得到词向量的质量如何。
而外在评估意思是通过一些具体的任务去得到它的性能评估，例如使用不同方法训练出来的词向量用作文本分类、命名实体识别之类的具体NLP任务，计算准确率、召回率、f1分数之类的指标来评估词向量的好坏。

---

参考资料

• https://www.jianshu.com/p/af8f20fe7dd3
• https://www.jianshu.com/p/d534570272a6
• https://www.cnblogs.com/DjangoBlog/p/6421536.html
• https://zhuanlan.zhihu.com/p/33138329
• https://nlp.stanford.edu/pubs/glove.pdf

标签：Embeddings,log,tilde,frac,https,Sense,Word,com,向量
来源： https://blog.csdn.net/sinat_29819401/article/details/90669304