奇怪的汉诺塔

题目描述

汉诺塔问题，条件如下：

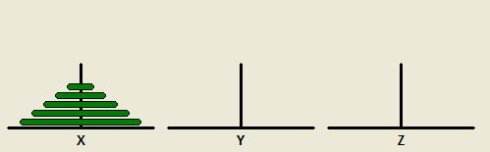
1、这里有A、B、C和D四座塔。

2、这里有n个圆盘，n的数量是恒定的。

3、每个圆盘的尺寸都不相同。

4、所有的圆盘在开始时都堆叠在塔A上，且圆盘尺寸从塔顶到塔底逐渐增大。

5、我们需要将所有的圆盘都从塔A转移到塔D上。

6、每次可以移动一个圆盘，当塔为空塔或者塔顶圆盘尺寸大于被移动圆盘时，可将圆盘移至这座塔上。

请你求出将所有圆盘从塔A移动到塔D，所需的最小移动次数是多少。

输出格式

对于每一个整数n(1≤n≤121≤n≤12),输出一个满足条件的最小移动次数，每个结果占一行。

题解：简单递归问题 ，思考：三座塔时：假设一共有n个圆盘，我们可以先将n - 1 个圆盘放到B处，再将第 n 个圆盘放到C处，再将 n - 1 个圆盘放到第n个圆盘的上面，即F[ n ] = F[ n - 1 ] * 2 + 1;
四座塔时，我们可以先把 i 个盘子在四塔模式下放到B柱上，再将 n - i 个盘子在三塔模式下放到C柱上，最后 i 个盘在四塔模式下放到D柱上，考虑所有的 i 可能取的最小值，得到递归式：
G[ i ] = min(G[i], 2 * G[ j ] + F[i - j])

代码如下：

#include<iostream>
#include<cstring>
using namespace std;
int f[15], d[15];
int main()
{
    d[1] = 1;
    for(int i = 2 ;i < 13; i++)
        d[i] = d[i - 1] * 2 + 1;
    memset(f, 0x3f, sizeof f);
    f[0] = 0;
    for(int i = 1 ; i< 13; i++){
        for(int j = 0; j < i; j++){
            f[i] = min(f[i], 2 * f[j] + d[i - j]);
        }
    }
    for(int i = 1; i < 13; i++)cout << f[i] <<endl;
    return 0;
}

标签：13,放到,圆盘,++,int,汉诺塔,柱上,奇怪
来源： https://blog.csdn.net/qq_43328040/article/details/89321519