Codeforces 题目选做
作者:互联网
CF1711D
令直接下大雨的点为关键点。
做法一:
首先有结论:对于发大水的点我们只需要考虑关键点即可。
证明:
对于两个相邻的关键点 \(x_i\) 和 \(x_j\) \((x_i<x_j)\) 。令他们的降水量分别为 \(p_i\) 和 \(p_j\) 。考虑中间的一个点 \(pos\) 。
那么考虑这两个关键点对这三个点的影响。
\(a_{x_i}=p_i+p_j-(x_j-x_i)\)
\(a_{pos}=p_i+p_j-(pos-x_i+x_j-pos)=p_i+p_j-(x_j-x_i)\)
\(a_{x_j}=p_i+p_j+(x_j-x_i)\)
因此两个关键点之间的点收到的影响是相同的,且和关键点的影响相同。
我们考虑求出所有关键点的降雨量,这一步可以用两次差分求出。
令 \(c_i=a_i-a_{i-1},d_i=c_i-c_{i-1}\) 。
那么一次降雨 \((x_i,p_i)\) 就可以拆解为:\(d_{x_i-p_i+1}:=d_{x_i-p_i+1}+1\\d_{x_i+1}:=d_{x_i+1}-2\\d_{x_i+p_i+1}:=d_{x_i+p_i+1}+1\) 。
然后做前缀和就可以求出来所有关键点的降水量了。
然后我们只用考虑所有 \(a_{i}>m\) 的关键点即可。对于一次降雨 \((x_j,p_j)\) ,若将其删去满足要求,那么有:\(a_i-(p_j-|x_i-x_j|)\le m\) 。把绝对值式子拆开:
\(\begin{cases}a_i-x_i\le m+p_j-x_j\\a_i+x_i\le m+p_j+x_j\end{cases}\)
对于每一个关键点可以求出 \(\max{(a_i-x_i)}\) 和 \(\max(a_i+x_i)\) 。那么对于任意一次降雨只有满足 \(m+p_j-x_j\ge max(a_i-x_i) \land m+p_j+x_j\ge max(a_i+x_i)\) 。那么才可能没有洪水出现。
复杂度:\(O(n\log n)\)
代码:Link
做法二:
其实前面求 \(a\) 值和做法一的做法是一样的。不过这个做法不是求出所有的关键点的值,而是求出所有极值的 \(a\) 值。(但其实是等价的,因为做法一中已经证明了中间的点一定不会比关键点大)。
我们依次枚举每一次降雨,那么这次降雨被删除后没有洪水,当且仅当所有下雨值都在蓝色的区域内(包括山顶以下的部分)。(图是贺的)/qd
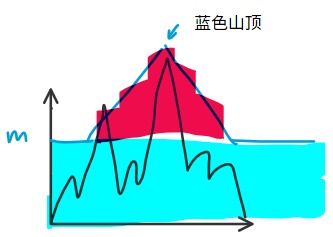
那么我们反过来思考,我们对于所有的极值,我们找到可以包括他的蓝色山顶应位于的区域。然后求所有极值的区域交。
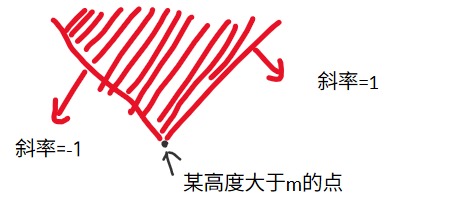
(红色区域就是蓝色山顶关于这个高度大于 \(m\) 的点应位于的区间。)
维护其实是简单的,维护两种斜率的直线就可以了(截距取 \(max\) ),具体见代码/kel。判断一个蓝色山顶的时候也可以直接转换为两条直线。
复杂度:\(O(n\log n)\)
代码:Link
CF1711E
因为有: \(x+y=(x\oplus y)+2(x\land y)\) ,所以可得:\((a\oplus b)+(a\oplus c)=(a\oplus b \oplus a\oplus c)+2((a\oplus b)\land (a\oplus c))=(b\oplus c)+2((a\oplus b)\land (a\oplus c))\) 。
显而易见的,后面的这个式子值是大于等于 \(0\) 的,所以 \((a\oplus b)+(a\oplus c)\) 一定不小于 \((b\oplus c)\) 。所以对于所有的数位只需要一位有 \((a\oplus b)+(a\oplus c)>(b\oplus c)\) 的情况就行了。考虑到这只考虑了 \(a\) 的情况,剩下两个轮换一下就可以了。
做的话直接数位 \(DP\) 。在 \(DP\) 中记录 \(7\) 个量,当前位置,\(a\) 是否达上限,\(b\) 是否达上限,\(c\) 是否达上限,是否已经有 \((a\oplus b)+(a\oplus c)>(b\oplus c)\) ,是否已经有 \((b\oplus a)+(b\oplus c)>(a\oplus c)\) ,是否已经有 \((c\oplus a)+(c\oplus b)>(a\oplus b)\) 。
复杂度: \(O(2^9n)\)
代码:Link
CF762F
主要参考了大象的题解 。
首先观察到数据范围 \(\mid S \mid \leq 1000,\mid T \mid \leq 12\) 。基本上就时状压了。
我们设 \(dp_{i,j}\) 表示 \(S\) 中用 \(i\) 和 \(i\) 的右兄弟匹配 \(T\) 中状态为 \(j\) 的方案数。
具体做的时候,我们直接钦定 \(S\) 的根为 \(1\) ,然后枚举 \(T\) 的根即可。整过过程可以使用记忆化搜索,这样会有很多状态其实根本没有用。
最后答案就是:\(S\) 与 \(T\) 同构的方案数 \(/\) \(T\) 自同构的方案数。
预处理的时候处理出来每个节点的所有儿子和 \(T\) 的儿子集合的状压表示。
复杂度:\(O(\mid T\mid ^2 \times 2^{\mid T\mid}\times \mid S \mid)\)
代码:Link
CF446C
区间加斐波那契是一件困难的事情。
但是斐波那契有通项公式:\(F_n=\dfrac{1}{\sqrt 5}((\dfrac{1+\sqrt 5}{2})^n-(\dfrac{1-\sqrt 5}{2})^n)\) 。而且 \(5\) 在模数 \(1e9+9\) 下也存在二次剩余。(\(\sqrt 5 \equiv 383008016\pmod{1e9+9}\))
那么我们直接把每次区间加斐波那契,改为区间加等比数列,因为公比是固定的,所以懒惰标记记录所有首项就可以了。
注意下传标记时,右儿子的标记要把左儿子的区间跨过去。
复杂度:\(\mathcal O(m\log n)\)
代码:Link
标签:选做,题目,max,复杂度,Codeforces,mid,Link,oplus,关键点 来源: https://www.cnblogs.com/Vitheon/p/16673931.html