P1399 [NOI2013] 快餐店 题解
作者:互联网
题目大意
求一棵基环树的重心。即一个点,使得树上到其距离最长的点到其的距离最短。注意,这个点不一定是一个节点,可以在树上的任意位置。输出树上到其距离最长的点到其的距离。
或者说求基环树最短的直径?(大雾
解题思路
显然,这颗基环树的直径只有两种情况:经过环和不经过环。
如果不经过环,那必定是环上某个点为根的子树的直径,这个可以用一般树上的做法做。再在所有的子树上的直径求最大值就是不经过环上的直径的答案。
重点在于环上的情况。首先我们画一个细菌一棵基环树,为了方便,我们默认这棵树上的边权为 \(1\),实际实现时只需要考虑上边权就行了:
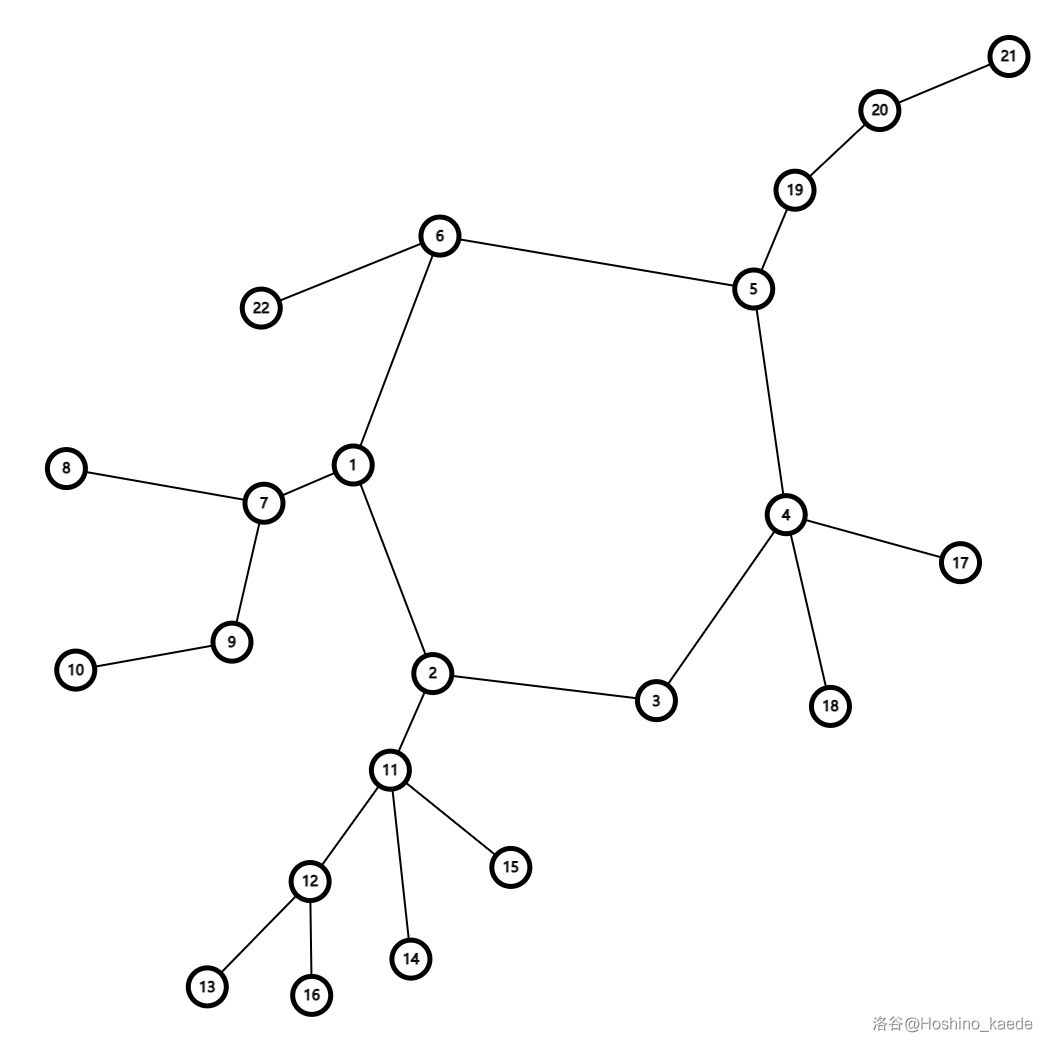
我们可以考虑枚举断开环上的哪一条边,再每种情况求一遍 \(\max\{dep_i + dep_j + dis(i,j)\}\),最后对每种情况的答案取最小值就是经过环山的直径了。其中 \(dep_i\) 表示环上第 \(i\) 个点的子树最大深度,\(dis(i,j)\) 表示环上第 \(i\) 个点和第 \(j\) 个点的距离。
这样不仅说起来拗口,时间复杂度也爆炸。
考虑有没有什么办法优化。首先,我们随便选择环上的一条边把环断开,这里选择的是 \(1\) 和 \(6\) 之间的边:
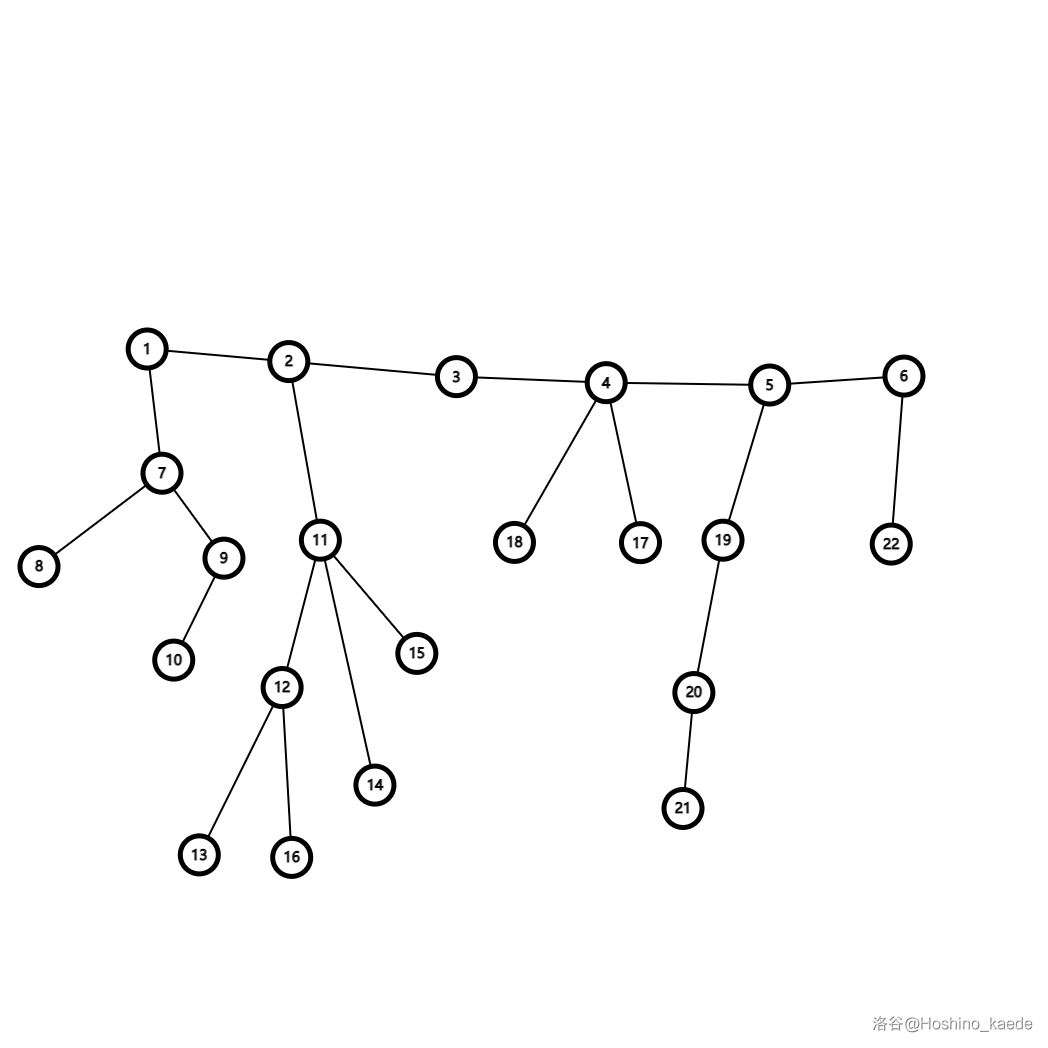
然后考虑枚举环上的点, 求出将环上第 \(i\) 个点和环上第 \(i + 1\) 个点之间的边断开后的直径,再取一个 \(\min\) 就是经过环上的答案了。
为了区分,我们把初始断开的边,即这里 \(1\) 和 \(6\) 之间的边成为初始断边,把当前枚举的要断开的边成为当前断边。
接下来又分情况考虑,总共有三种情况:
-
起点和终点都在当前断边左边。
-
起点和终点都在当前断边右边
-
起点和终点一个在当前断边左边,一个在当前断边右边,即直径经过了初始断边。
其中前两种情况又是类似的,我们详细讲第一种:
我们设 \(c_i\) 表示两段在环上第 \(i\) 个点或第 \(i\) 个点之前的点为根的子树上,且至少经过了环上一条边的直径长度,也就是我们要求的第一种情况的直径长度。这个不太好求,我们先稍微修改一下定义: \(c_i\) 表示起点第 \(i\) 个点之前的点为根的子树上,终点在以环上第 \(i\) 个点为根的子树上,且至少经过了环上一条边的直径长度。显然会有柿子:
\[c_i = \max_{1 \le j \le i}\{dep_i + dep_j + dis(i,j)\} \]显然,直接枚举又是 \(O(TLE)\) 的,我们想办法优化。
首先一个优化空间在于 \(dis(i,j)\),求这个如果暴力的话时间肯定承受不住,我们可以考虑求一个距离前缀和,\(pre_i\) 表示从环上第 \(1\) 个点到环上第 \(i\) 个点的距离,那么 \(dis(i,j) = |pre_i - pre_j|\)。则柿子变为:
\[c_i = \max_{1 \le j \le i}\{dep_i + dep_j + pre_i - pre_j\} \]然而,这样依旧 \(O(n^2)\)。剩下的优化空间就只有枚举的时间了,首先移项,得到:
\[c_i = \max_{1 \le j \le i}\{(dep_i + pre_i) + (dep_j - pre_j)\} \]\(dep_i + pre_i\) 显然在 \(i\) 固定的时候是定值,把它丢出来:
\[c_i = \max_{1 \le j \le i}\{(dep_j - pre_j)\} + (dep_i + pre_i) \]那么中间的 \(dep_j - pre_j\) 我们可以变枚举 \(i\) 边维护,这样就是 \(O(n)\) 的了。
于是我们在回到一开始要求的东西,只需要对算出来的 \(c\) 求一个前缀最大值就好了。
第二种情况与第一种情况对称。我们设 \(d_i\) 表示两段在环上第 \(i\) 个点或第 \(i\) 个点之前后的点为根的子树上,且至少经过了环上一条边的直径长度。它的求法相同,只需要求后缀最大值和距离的后缀和就好了。
即,设 \(suf_i\) 表示从环上最后一个点到环上第 \(i\) 个点之间的距离,在经过与上面类似的简化后,有:
\[d_i = \max_{i \le j \le t}\{(dep_j - suf_j)\} + (dep_i + suf_i) \]其中 \(t\) 表示环上的结点数量,也代表环上最后一个点。
然后求后缀最大值,就得到了我们第二种情况的答案。
如图,但 \(i = 3\) 时,\(c_i\) 和 \(d_i\) 本别代表了图中蓝色路径得长度和紫色路径得长度:
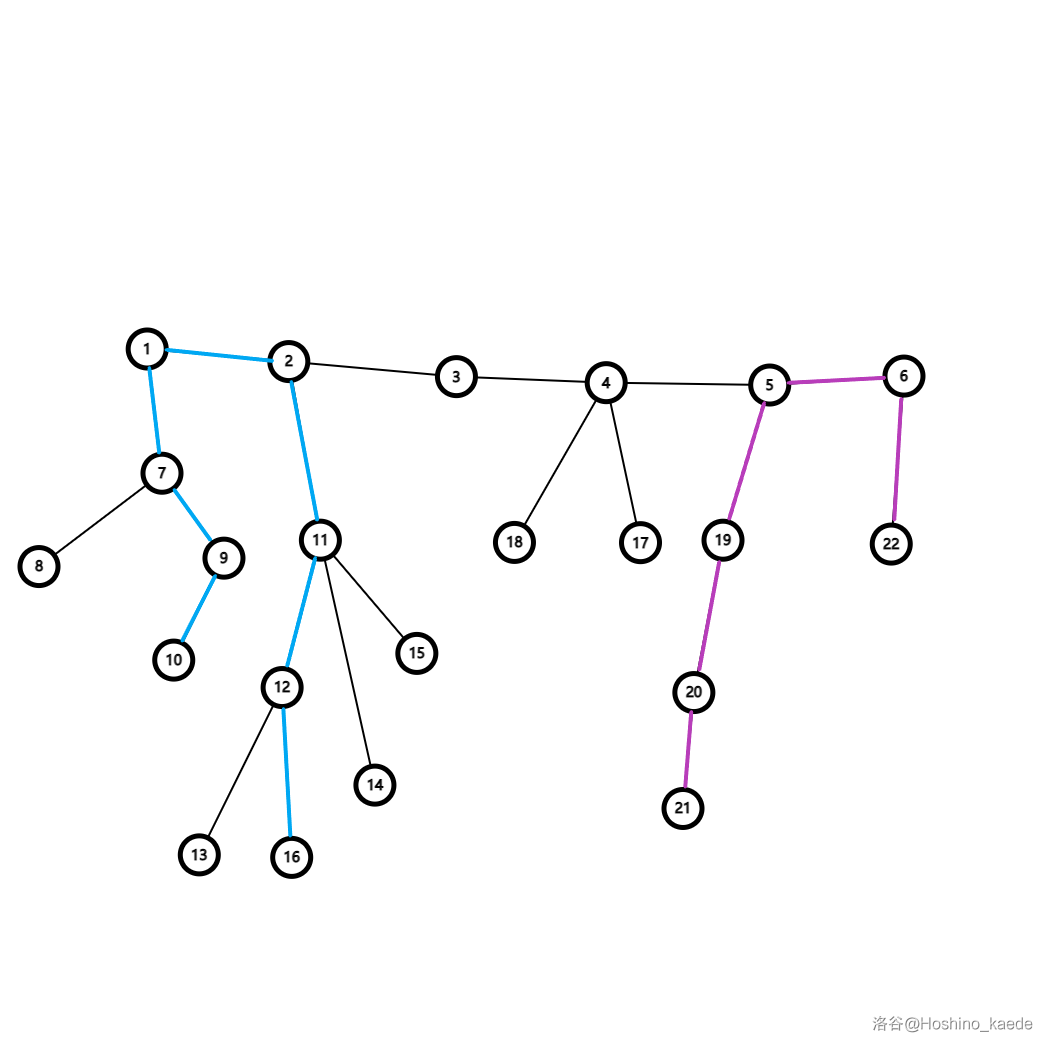
有一些细节需要注意,假设我们当前断边是环上第 \(i\) 个点和环上第 \(i + 1\) 个点之间的边,那么前两种情况的答案应该是 \(c_i\) 和 \(d_{i + 1}\) 而非 \(c_i\) 和 \(d_i\)。
至于第三种情况稍微复杂一点,我们维护两个数组,\(a_i\) 和 \(b_i\)。其中 \(a_i\) 表示以环上第一个点为起点,以环上第 \(i\) 个点或环上第 \(i\) 个点以前的点为根的子树中某一点为终点的最大长度;\(b_i\) 表示以环上最后一个点为起点,以环上第 \(i\) 个点或环上第 \(i\) 个点以后的点为根的子树中某一点为终点的最大长度。
经过上面的套路我们知道,对于 \(a_i\),可以先求出以环上第一个点为起点,以环上第 \(i\) 个点的子树中某一点为终点的最大长度,也就是 \(pre_i + dep_i\),再求前缀最大值;\(b_i\) 则是求出以环上最后一个点为起点,以环上第 \(i\) 个点为根的子树中某一点为终点的最大长度,即 \(suf_i + dep_i\),再求后缀最大值。
如图,\(a_i\) 和 \(d_i\) 分别代表图中的橙色路径长度和红色路径长度。
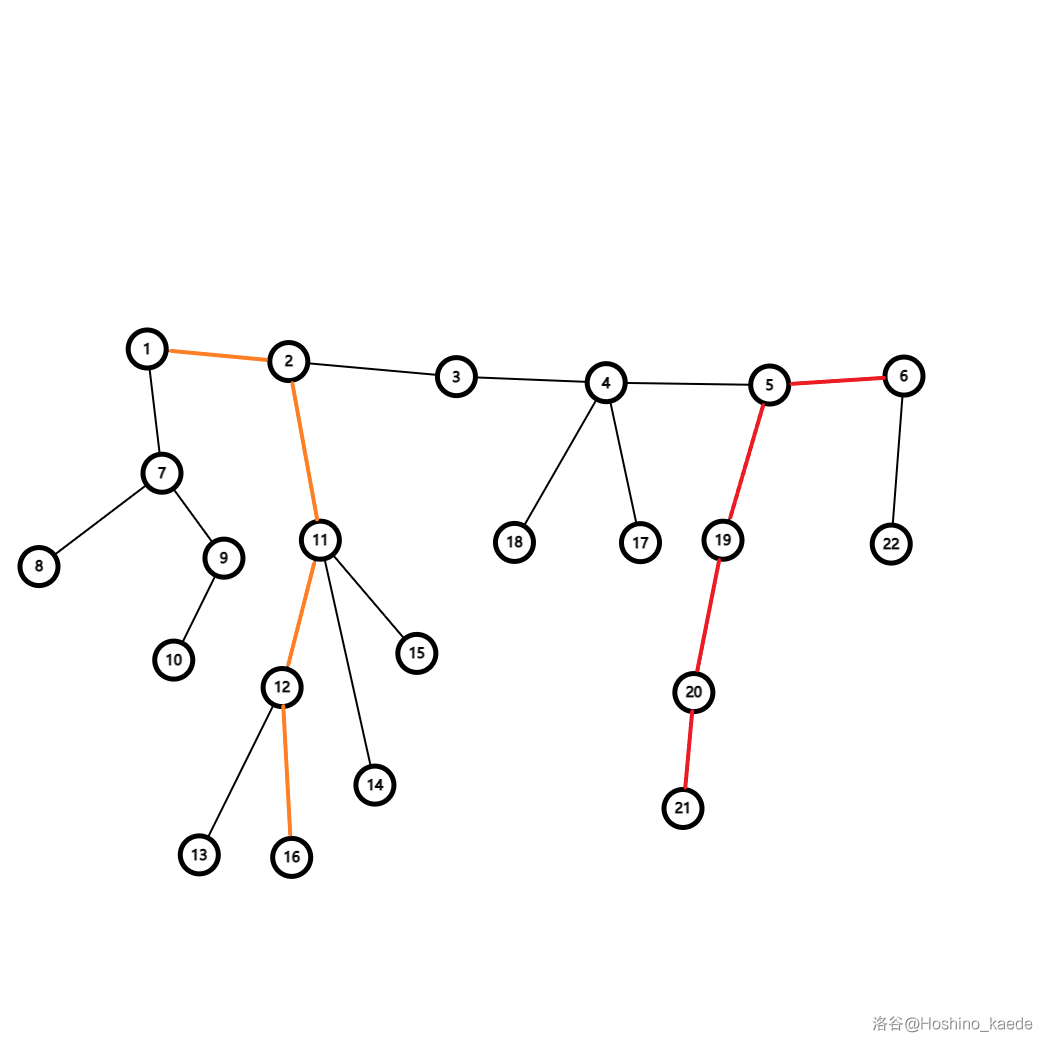
那么第三种情况的答案就是红色路径长度加上橙色路径的长度再加上初始断边,即这里 \(1\) 和 \(6\) 之间的边的长长度。
这三种情况取最大值,就是将环上第 \(i\) 个点和环上第 \(i + 1\) 个点之间的边断开后的答案。接着枚举 \(i\) 再求最小值,这就是直径经过环上的答案。
这种情况与之前直径不经过环上的答案取 \(\max\) 就是这颗基环树的直径了。
对于这一题来说,答案还需要除以二。
完整代码
提供一些错误经验。
如果你 TLE,记得把 memset 换成时间戳。
如果你 WA 30pts,大概是没有开 long long。
如果你 WA 50pts,大概是 INF 开小了。
如果你 WA 90pts,大概是某些数组没有取前缀最大值或者后缀最大值。
没有删除调试行,如果需要的话可以对照一下输出。
#include<bits/stdc++.h>
#define MAXN 100010
#define INF 0x7f7f7f7f7f7f7f7f
using namespace std;
typedef long long ll;
struct node{ ll id, dis; };
struct edge{ ll pre, to, w; };
stack<node> s;
node cir[MAXN];
edge e[MAXN << 1];
ll n, m, ans1, ans2 = INF, cnt = 1, times = 1;
ll head[MAXN], dis[MAXN], dia[MAXN], dep[MAXN], pre[MAXN], suf[MAXN], vis[MAXN], a[MAXN], b[MAXN], c[MAXN], d[MAXN];
bool iscir[MAXN];
inline ll read(){
ll s = 0, w = 1;
char ch = getchar();
while(ch < '0' || ch > '9') { if(ch == '-') w = -1; ch = getchar(); }
while(ch >= '0' && ch <= '9') s = s * 10 + ch - '0', ch = getchar();
return s * w;
}
void add_edge(ll u, ll v, ll w){
e[++cnt].pre = head[u];
e[cnt].to = v; e[cnt].w = w;
head[u] = cnt;
}
bool find_circle(ll now, ll fr){
s.push((node){now, e[fr].w}); vis[now] = times;
for(int i = head[now]; i; i = e[i].pre){
// printf("%lld -> %lld i = %lld fr = %lld %lld\n",now,e[i].to,i,fr,i ^ 1 == fr);
if((i ^ 1) == fr) continue;
// printf("*\n");
if(vis[e[i].to] != times){
if(find_circle(e[i].to, i)) return true;
}else{
while(s.top().id != e[i].to){
node p = s.top(); s.pop();
cir[++m] = p; iscir[p.id] = true;
}
cir[++m] = (node){e[i].to, e[i].w}; iscir[e[i].to] = true;
s.pop();
return true;
}
}
s.pop();
return false;
}
ll bfs(ll st){
// memset(vis, 0, sizeof(vis));
// memset(dis, 0, sizeof(dis));
ll res = st; times++;
queue<ll> q; q.push(st);
dis[st] = 0; vis[st] = times;
while(!q.empty()){
ll now = q.front(); q.pop();
for(int i = head[now]; i; i = e[i].pre){
if(vis[e[i].to] != times && !iscir[e[i].to]){
// printf(" %lld -> %lld\n",now,e[i].to);
dis[e[i].to] = dis[now] + e[i].w;
if(dis[e[i].to] > dis[res]) res = e[i].to;
q.push(e[i].to); vis[e[i].to] = times;
}
}
}
return res;
}
int main(){
scanf("%lld",&n);
for(int i = 1; i <= n; i++){
ll u = read(), v = read(), w = read();
add_edge(u, v, w); add_edge(v, u, w);
}
find_circle(1, 0);
for(int i = 1; i <= m; i++){
iscir[cir[i].id] = false;
ll p = bfs(cir[i].id);
dep[i] = dis[p]; dia[i] = dis[bfs(p)];
ans1 = max(ans1, dia[i]);
iscir[cir[i].id] = true;
}
for(int i = 2; i <= m; i++) pre[i] = pre[i - 1] + cir[i - 1].dis;
for(int i = m - 1; i >= 1; i--) suf[i] = suf[i + 1] + cir[i].dis;
for(int i = 1; i <= m; i++) a[i] = max(a[i - 1], dep[i] + pre[i]);
for(int i = m; i >= 1; i--) b[i] = max(b[i + 1], dep[i] + suf[i]);
for(ll i = 1, mx = 0; i <= m; i++){
c[i] = mx + pre[i] + dep[i];
mx = max(mx, dep[i] - pre[i]);
}
for(ll i = m, mx = 0; i >= 1; i--){
d[i] = mx + suf[i] + dep[i];
mx = max(mx, dep[i] - suf[i]);
}
for(int i = 1; i <= m; i++) c[i] = max(c[i], c[i - 1]);
for(int i = m; i >= 1; i--) d[i] = max(d[i], d[i + 1]);
for(int i = 1; i < m; i++){
ll res = max(a[i] + b[i + 1] + cir[m].dis, max(c[i], d[i + 1]));
ans2 = min(ans2, res);
}
printf("%.1lf\n",(double)max(ans1, ans2) / 2.0);
// printf("iscir: "); for(int i = 1; i <= n; i++) printf("%lld ",iscir[i]); printf("\n");
// printf("cir_id: "); for(int i = 1; i <= m; i++) printf("%lld ",cir[i].id); printf("\n");
// printf("cir_dis: "); for(int i = 1; i <= m; i++) printf("%lld ",cir[i].dis); printf("\n");
// printf("dia: "); for(int i = 1; i <= m; i++) printf("%lld ",dia[i]); printf("\n");
// printf("dep: "); for(int i = 1; i <= m; i++) printf("%lld ",dep[i]); printf("\n");
// printf("pre: "); for(int i = 1; i <= m; i++) printf("%lld ",pre[i]); printf("\n");
// printf("suf: "); for(int i = 1; i <= m; i++) printf("%lld ",suf[i]); printf("\n");
// printf("a: "); for(int i = 1; i <= m; i++) printf("%lld ",a[i]); printf("\n");
// printf("b: "); for(int i = 1; i <= m; i++) printf("%lld ",b[i]); printf("\n");
// printf("c: "); for(int i = 1; i <= m; i++) printf("%lld ",c[i]); printf("\n");
// printf("d: "); for(int i = 1; i <= m; i++) printf("%lld ",d[i]); printf("\n");
return 0;
}
标签:pre,max,环上,P1399,dep,题解,NOI2013,dis,个点 来源: https://www.cnblogs.com/Elfin-Xiao/p/16626376.html