题目简介

有点长：

火星小镇上有\(n\)个居民（编号\(1,2,……,n\)）。机器学习算法预测出这些居民在接下来\(T\)个时刻（编号\(1,2,……,T\)）的生死情况，每条预测都是如下两种形式之一：

• 难兄难弟\(0\) \(t\) \(x\) \(y\)：在\(t\)时刻，如果\(x\)是死亡状态，那么在\(t+1\)时刻，\(y\)是死亡状态。（注意，当\(x\)在\(t\)时刻是生存状态时，该预测也被认为是正确的）；
• 死神来了\(1\) \(t\) \(x\) \(y\)：在\(t\)时刻，如果\(x\)是生存状态，那么在\(t\)时刻，\(y\)是死亡状态。（注意，当\(x\)在\(t\)时刻是死亡状态时，该预测也被认为是正确的）。

注意本题是对某个时刻进行生死状态的预测，如果某个人在\(t\)时刻是生存状态，在\(t+1\)时刻是死亡状态，你可以认为是在\(t\)到\(t+1\)这段时间内发生了某个事件导致其死亡。

虽然 JYY 对自己从大数据中统计得到的模型非常自信，但火星人看到这些预测吓了一跳，表示实在难以接受这种设定，更是认为计算机科学是可怕的邪教，打破了他们平静的生活。为了安抚火星人的情绪， JYY 打算从这些预测结果中推导出一些火星人更容易接受的事实，从而安抚火星人的情绪。

具体来说，JYY 首先假设对火星人生死的预测全部正确，在此基础上，JYY 希望为小镇上的每个居民\(k\)分别计算有多少个火星人有可能和他一起活到第\(T+1\)时刻，换言之，JYY 希望为每个火星人\(k\)计算

\[\sum_{1 \leq i \leq n,i \neq k} \operatorname{Live}(k,i) \]

其中 \(\operatorname{Live}(i,j)=1\) 表示编号为\(i\)和\(j\)的火星人有可能同时在第 \(T+1\) 时刻处于生还状态，否则\(\operatorname{Live}(i,j)=0\)。

注意火星人是不能够复活的。一个火星人可能在时刻\(1\)就处于死亡状态，也有可能有预测未覆盖的死亡情况发生（火星人在任何时候都可能死亡，但任意时刻观察到火星人的状态要么活着，要么死亡）。最后，注意到\(\operatorname{Live}\)是为每一对火星人分别独立计算的，因此\(\operatorname{Live}(x,y)=1,\operatorname{Live}(y,z)=1\)并不意味着\(\operatorname{Live}(x,z)=1\)。

分析

考试时接近想出了连边的方法，可是没有考虑全导致图中出现了 \(\mbox{SCC}\) ，最后爆零（T_T）。

由于本蒟蒻鄙陋没学过 \(2-\mbox{SAT}\) ，所以采用相对简单的方式来叙述吧。

考虑有一个人 \(x\) ，\(\mbox{TA}\) 在时刻 \(t\) 的状态只可能有两种：\(\mbox{Alive}(x,t)\) 或者 \(\mbox{Dead}(x,t)\)，为了方便，记作 \(\mbox A(x,t)\) 和 \(\mbox D(x,t)\)

考虑有两个状态 \(A\) 和 \(B\) ，状态 \(A\) 能推出状态 \(B\) 记作 \(A\to B\)。

根据题目的预言含义：

• 0 t x y 表示存在 \(\mbox D(x,t)\) 那么则有 \(\mbox D(y,t+1)\) 。相应的，如果有 \(A(y,t+1)\) ，则不存在 \(\mbox D(x,t)\) ，那么只存在 \(\mbox A(x,t)\) 。将他们记作 \(\mbox D(x,t)\to \mbox D(y,t+1)\)，\(A(y,t+1)\to A(x,t)\)
• 1 t x y 表示存在 \(\mbox A(x,t)\) 那么则有 \(\mbox D(y,t)\) 。相应的，如果有 \(\mbox A(y,t)\) ，那么一定只有 \(\mbox D(x,t)\)。将他们记作 \(\mbox A(x,t)\to D(y,t)\) ，\(\mbox A(y,t)\to D(x,t)\)
• 不要忘记了，死亡之后不能复活。这一条我们可以记为 \(\mbox D(x,t)\to \mbox D(x,t+1)\) ，相应的，有 \(\mbox A(x,t+1)\to \mbox A(x,t)\)

另外，"火星人随时有可能死去" 这一条我们并没有记录，因为这并不是必然结论。我们要尽量使最后 \(\mbox{Dead}\) 的状态数最少。

我们直接按照这种方式建图，会发现点的总个数是 \(n\times(T+1)\) （最后 \(T+1\) 的状态也算）。空间显然过不去。我们将那些无效的点（没有路径分支的点）删去，只留下输入中的 \(n+m\) 个点。具体操作是使用 set 和 map 。

接着我们开始在图上跑，已知的条件是 \(\mbox A(x,T+1)\)，我们看它还能到达哪些状态。具体的操作就是用一个bitset 优化，枚举初始位置 \(\mbox A(x,T+1 )\) 然后 \(\mbox{DFS}\)。其中 bitset 变量 sta[x] 的第 \(i\) 位为 \(0\) 表示状态 \(x\) 不能走到 \(\mbox D(i)\) ，为 \(1\) 表示能走到 \(\mbox D(i)\)。很显然我们有：

\[sta[x]=sta[x]\ \mbox{or}\ sta[y](y\in \mbox{son}[x]) \]

最后的 \(Ans[i]=n-\)以 \(A(i,T+1)\) 为起点能到达的 \(\mbox{dead}\) 状态数\(-1\) 。注意，如果某一个 \(A(x,T+1)\) 能够到达 \(D(x,T+1)\) ，那么我们称这个点为 必死点 。必死点的 \(Ans\) 为 \(0\) ，且要计入其他点能到达的 \(\mbox{dead}\) 状态数。

只是点这么多，bitset 显然存不下。所以我们来一发秀操作，对这 \(n+m\) 个点分块处理。另 \(B\) 为每一块的大小，我们依次计算 \([1,B]\) 的 \(\mbox{Ans}\) ，\([B+1,2B]\) 的 \(\mbox{Ans}\) ……

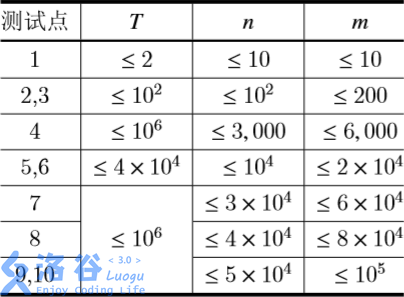
\(B\approx 10^4\) 时可以通过。

\(AC\ Code\)

#include<bitset>
#include<cstdio>
#include<cstring>
#include<functional>
#include<iostream>
#include<map>
#include<set>
using namespace std;
const int Maxn=5e4+5;
const int Maxm=1e5+5;
const int Maxv=1e6;
const int B=1e4;
struct adjacency_list{int nxt,t;}g[Maxv];
int h[Maxv];
int tot;
void add(int x,int y){g[++tot]={h[x],y};h[x]=tot;}
int c[Maxm],t[Maxm],a[Maxm],b[Maxm];
set<int>s[Maxn];
map<int,int>id[Maxn][2];
int al[Maxn],de[Maxn];// 记录 A(x,T+1) 和 D(x,T+1)
int rev[Maxv];
bool vis[Maxv];
bool dea[Maxn];
bitset<B>sta[Maxv];
bitset<B>cur;
int ans[Maxn];
void dfs(int x,int L,int R){
	if(vis[x])return ;vis[x]=1;
	sta[x].reset();
	if(L<=rev[x]&&rev[x]<=R)sta[x].set(rev[x]-L);// 在查询范围内，记录。
	for(int i=h[x];i;i=g[i].nxt){
		int y=g[i].t;dfs(y,L,R);
		sta[x]|=sta[y];
	}
}
int main(){
	int T,n,m;cin>>T>>n>>m;
	for(int i=1;i<=m;++i){
		cin>>c[i]>>t[i]>>a[i]>>b[i];
		s[a[i]].insert(t[i]);
	}
	int cnt=0;
	for(int i=1;i<=n;++i){
		s[i].insert(T+1);
		for(auto x:s[i])id[i][0][x]=++cnt,id[i][1][x]=++cnt;// 给每个点重新编号
		auto nxt=[](auto it){return ++it;};
		for(auto it=s[i].begin();it!=s[i].end()&&nxt(it)!=s[i].end();++it)
			add(id[i][0][*it],id[i][0][*nxt(it)]),// D(x,t)->D(x,t+1)
			add(id[i][1][*nxt(it)],id[i][1][*it]);// A(x,t+1)->A(x,t)
	}
	for(int i=1;i<=m;++i)
		if(c[i]){
			int x=*s[b[i]].lower_bound(t[i]);
			add(id[a[i]][1][t[i]],id[b[i]][0][x]);// A(x,t)->D(x,t)
			add(id[b[i]][1][x],id[a[i]][0][t[i]]);// A(x,t)->D(x,t)
		}else {
			int x=*s[b[i]].upper_bound(t[i]);
			add(id[a[i]][0][t[i]],id[b[i]][0][x]);// D(x,t)->D(x,t+1)
			add(id[b[i]][1][x],id[a[i]][1][t[i]]);// A(x,t+1)->A(x,t)
		}
	for(int i=1;i<=n;++i)al[i]=id[i][1][T+1],de[i]=id[i][0][T+1],rev[de[i]]=i;
	for(int l=1;l<=n;l+=B){
		int r=min(l+B-1,n);memset(vis,0,sizeof vis);
		for(int i=1;i<=n;++i)dfs(al[i],l,r);
		cur.reset();// 用于记录必死点
		for(int i=l;i<=r;++i)
			if(sta[al[i]][i-l])dea[i]=1,cur.set(i-l);// 判断是否为必死点
		for(int i=1;i<=n;++i)ans[i]+=(r-l+1)-(cur|sta[al[i]]).count();// 获取Ans
	}
	for(int i=1;i<=n;++i)cout<<(dea[i]?0:ans[i]-1)<<' ';
	cout<<'\n';
	return 0;
} 

$$-----EOF-----$$

标签：状态,火星人,预测,int,JSOI2019,时刻,mbox,id,精准
来源： https://www.cnblogs.com/wintersunny/p/16518829.html