【模板】轻重链剖分/树链剖分

题目描述

如题，已知一棵包含 \(N\) 个结点的树（连通且无环），每个节点上包含一个数值，需要支持以下操作：

• 1 x y z，表示将树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值都加上 \(z\)。

• 2 x y，表示求树从 \(x\) 到 \(y\) 结点最短路径上所有节点的值之和。

• 3 x z，表示将以 \(x\) 为根节点的子树内所有节点值都加上 \(z\)。

• 4 x 表示求以 \(x\) 为根节点的子树内所有节点值之和

输入格式

第一行包含 \(4\) 个正整数 \(N,M,R,P\)，分别表示树的结点个数、操作个数、根节点序号和取模数（即所有的输出结果均对此取模）。

接下来一行包含 \(N\) 个非负整数，分别依次表示各个节点上初始的数值。

接下来 \(N-1\) 行每行包含两个整数 \(x,y\)，表示点 \(x\) 和点 \(y\) 之间连有一条边（保证无环且连通）。

接下来 \(M\) 行每行包含若干个正整数，每行表示一个操作。

输出格式

输出包含若干行，分别依次表示每个操作 \(2\) 或操作 \(4\) 所得的结果（对 \(P\) 取模）。

样例 #1

样例输入 #1

5 5 2 24
7 3 7 8 0 
1 2
1 5
3 1
4 1
3 4 2
3 2 2
4 5
1 5 1 3
2 1 3

样例输出 #1

2
21

提示

【数据规模】

对于 \(30\%\) 的数据： \(1 \leq N \leq 10\)，\(1 \leq M \leq 10\)；

对于 \(70\%\) 的数据： \(1 \leq N \leq {10}^3\)，\(1 \leq M \leq {10}^3\)；

对于 \(100\%\) 的数据： \(1\le N \leq {10}^5\)，\(1\le M \leq {10}^5\)，\(1\le R\le N\)，\(1\le P \le 2^{31}-1\)。

【样例说明】

树的结构如下：

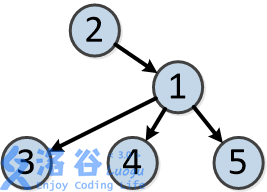
各个操作如下：

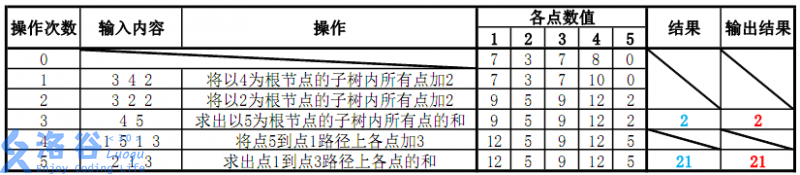
故输出应依次为 \(2\) 和 \(21\)。

树剖板子题
根据结点的轻重儿子，可以把整棵树树唯一地剖成若干个重链和若干个轻链
剖分后的某些性质：
1、并且每个结点都属于且仅属于一条重链
2、每条重链上的结点dfs序连续
3、每个结点及其子树的dfs序连续
性质1和性质2使得我们可以用线段树高效地维护整棵树，比如修改和查询两个结点之间简单路径的权值
性质3可以将本题的操作3、4转化为线段树的区间修改和查询

#include<bits/stdc++.h>
using namespace std;

#define fr first
#define se second
#define et0 exit(0);
#define rep(i, a, b) for(int i = (int)(a); i <= (int)(b); i ++)
#define rrep(i, a, b) for(int i = (int)(a); i >= (int)(b); i --)

typedef long long LL;
typedef pair<int, int> PII;
typedef pair<LL, LL> PLL;
typedef unsigned long long ULL;

const int INF = 0X3f3f3f3f, N = 1e5 + 10, M = 2 * N;
const double eps = 1e-7, PI = 3.1415926;

int n,m,root,MOD;
int w[N];

int head[N], idx;

struct EGDE{
	int to,next;
}eg[M];

void add(int x, int y)
{
	eg[idx].to=y;
	eg[idx].next=head[x];
	head[x]=idx++;
}

//Heavy-light Decomposition STARTS FORM HERE
int siz[N];//number of son
int son[N];//heavy son of the node
int faz[N];//father of the node
int dep[N];//depth of the node
int top[N];//top of the heavy link
int tid[N];//ID -> DFSID
int rnk[N];//DFSID -> ID
int cnt;//时间戳

void dfs_1(int cur,int fa,int depth){
	siz[cur]=1;
	faz[cur]=fa;
	dep[cur]=depth;
	for(int i=head[cur];~i;i=eg[i].next){
		int to=eg[i].to;
		if(to==fa) continue;
		dfs_1(to,cur,depth+1);
		siz[cur]+=siz[to];
		if(son[cur]==-1 || siz[son[cur]]<siz[to]) son[cur]=to;
	}
}

void dfs_2(int cur,int tp){
	top[cur]=tp;
	tid[cur]=++cnt;
	rnk[cnt]=cur;
	
	if(son[cur]==-1) return;
	dfs_2(son[cur],tp);
	
	for(int i=head[cur];~i;i=eg[i].next){
		int to=eg[i].to;
		if(to!=son[cur] && to!=faz[cur]) dfs_2(to,to);
	}
}

struct NODE{
	int l,r;
	int sum;
	int lazy;
}tr[N*4];

void pushup(int u){
	tr[u].sum=((LL)tr[u<<1].sum+tr[u<<1|1].sum)%MOD;
}

void pushdown(int u){
	int x=u<<1,y=u<<1|1;
	int lazy=tr[u].lazy;
	tr[x].sum=((LL)tr[x].sum+lazy*(tr[x].r-tr[x].l+1))%MOD;
	tr[x].lazy=((LL)tr[x].lazy+lazy)%MOD;
	tr[y].sum=((LL)tr[y].sum+lazy*(tr[y].r-tr[y].l+1))%MOD;
	tr[y].lazy=((LL)tr[y].lazy+lazy)%MOD;
	tr[u].lazy=0;
}

void build(int u,int l,int r){
	if(l==r){
		tr[u]={l,l,w[rnk[l]],0};
		return;
	}
	tr[u].l=l,tr[u].r=r;
	int mid=l+r>>1;
	build(u<<1,l,mid);
	build(u<<1|1,mid+1,r);
	pushup(u);
}

int query(int u,int l,int r){
	if(l<=tr[u].l && r>=tr[u].r) return tr[u].sum;
	else{
		pushdown(u);
		int mid=tr[u].l+tr[u].r>>1;
		if(r<=mid) return query(u<<1,l,r);
		else if(l>mid) return query(u<<1|1,l,r);
		else{
			int suml=query(u<<1,l,r),sumr=query(u<<1|1,l,r);
			return (LL)(suml+sumr)%MOD;
		}
	}
}

void modify(int u,int l,int r,int d){
	if(l<=tr[u].l && r>=tr[u].r){
		tr[u].sum=((LL)tr[u].sum+(tr[u].r-tr[u].l+1)*d)%MOD;
		tr[u].lazy=(LL)(tr[u].lazy+d)%MOD;
	}
	else{
		pushdown(u);
		int mid=tr[u].l+tr[u].r>>1;
		if(r<=mid) modify(u<<1,l,r,d);
		else if(l>mid) modify(u<<1|1,l,r,d);
		else{
			modify(u<<1,l,r,d);
			modify(u<<1|1,l,r,d);
		}
		pushup(u);
	}
}

int query_path(int x,int y){
	int res=0;
	int fx=top[x],fy=top[y];
	while(fx!=fy){
		if(dep[fx]>=dep[fy]){
			res=((LL)res+query(1,tid[fx],tid[x]))%MOD;
			x=faz[fx];
		}
		else{
			res=((LL)res+query(1,tid[fy],tid[y]))%MOD;
			y=faz[fy];
		}
		fx=top[x],fy=top[y];
	}
	
	if(x!=y){
		if(tid[x]<tid[y]) res=((LL)res+query(1,tid[x],tid[y]))%MOD;
		else res=((LL)res+query(1,tid[y],tid[x]))%MOD;
	}
	else res=((LL)res+query(1,tid[x],tid[y]))%MOD;
	
	return res;
}

void modify_path(int x,int y,int z){
	int fx=top[x],fy=top[y];
	while(fx!=fy){
		if(dep[fx]>=dep[fy]){
			modify(1,tid[fx],tid[x],z);
			x=faz[fx];
		}
		else{
			modify(1,tid[fy],tid[y],z);
			y=faz[fy];
		}
		fx=top[x],fy=top[y];
	}
	
	if(x!=y){
		if(tid[x]<tid[y]) modify(1,tid[x],tid[y],z);
		else modify(1,tid[y],tid[x],z);
	}
	else modify(1,tid[x],tid[y],z);
}

void work() {
	memset(head,-1,sizeof head);
	memset(son,-1,sizeof son);
	cin>>n>>m>>root>>MOD;
	rep(i,1,n) cin>>w[i];
	rep(i,1,n-1){
		int x,y;
		cin>>x>>y;
		add(x,y),add(y,x);
	}
	dfs_1(root,-1,0);
	dfs_2(root,root);
	build(1,1,cnt); 
	while(m--){
		int op,x,y,z;
		cin>>op;
		if(op==1){
			cin>>x>>y>>z;
			modify_path(x,y,z);
		}
		else if(op==2){
			cin>>x>>y;
			cout<<query_path(x,y)<<endl;
		} 
		else if(op==3){
			cin>>x>>z;
			int tdx=tid[x],tdy=tid[x]+siz[x]-1;
			modify(1,tdx,tdy,z);
		}
		else{
			cin>>x;
			int tdx=tid[x],tdy=tid[x]+siz[x]-1;
			cout<<query(1,tdx,tdy)<<endl;
		}
	}
}

signed main() {
	int test=1;
//	cin >> test;
	
	while (test--) {
		work();
	}
	
	return 0;
}

标签：链剖分,结点,洛谷,cur,剖分,int,tr,leq,tid
来源： https://www.cnblogs.com/xhy666/p/16508345.html