P1600 天天爱跑步 题解 Treap启发式合并
作者:互联网
仔细看了题解区里面好像平衡树的解法写的不太清楚,网上资料更是寥寥无几,经过自己的摸索之后,我尽量写一篇清楚的题解。
统一变量
设路径 \(i\) 的起点和终点为 \(s_i\) 和 \(t_i\), 长度为 \(dis_i\),起点和终点的lca为 \(lc_i\).
节点 \(i\) 深度为 \(d_i\).
推柿子
像其他题解所说的一样,我们将一条路径分为上行和下行的两段,找到当路径对观察员 \(u\) 有贡献时的等量关系。
我们可以发现,在 lca 靠 \(s\) 一侧(上行),
\(d_s=w_u + d_u\).
同理,在靠 \(t\) 一侧(下行),可以得到
\(d_t-dis =d_u-w_u\)
其中 \(dis\) 为 \(t\) 的路径的长度。
两个式子的左边都可以方便地存进平衡树维护。
两个式子的右边都可以方便地在 dfs 时取得。
可以证明,只有满足这两个条件,点 \(s\) 和 \(t\) 才会被观察者 \(u\) 观测到,是为必要条件。
做法
因此我们
- 写一个 lca 用于拆分路径.
- 在每一个点处开一颗平衡树(我用的 treap)。
- 在每一个点处开一个 vector 作为(所谓)差分数组。
对于上行侧的处理如下:
dfs前,我们先在每一个点 \(s\) 的平衡树加入一个 \(d_s\). 在 \(s\) 和 \(t\) 的 lca 处的 vector 也加入一个 \(d_s\).
在 dfs 时,首先递到叶子,归回到一节点 \(u\) 时,启发式地合并所有 \(u\) 的子节点的平衡树到 \(u\) 的平衡树。结果是,我们得到了包含 \(u\) 的子树的所有 \(d\) 信息的一棵平衡树。
插入:
启发式合并:合并的时候将 \(size\) 小的树的每一个点分别插入到到 \(size\) 大的树中。启发式合并比起任意合并是更优的,因为对于被合并的树,每次虽然都遍历了它的每一个点,但是每次合并得到的新树 \(size\) 都是小树的两倍以上。可得启发式合本身并的时间复杂度最多为 \(O(n \operatorname{log}n)\). 如果计算平衡树本身的复杂度,还要再乘以一个 \(\operatorname{log}n\).
由我们前面推的式子,对于上行,应读取在 \(u\) 的平衡树中,\(w_u + d_u\) 出现了多少次,观察点 \(u\) 的答案加上次数。
这时候来到了 vector 大展身手的时候。我们感性理解发现,每一条路径,在 lca 以上就无法产生贡献,那是因为路径不经过 lca 以上的点。
但是按照我们的启发式合并,所有的点信息都会毫无保留地被合并到根节点的平衡树,算出很多多余的答案。见图:
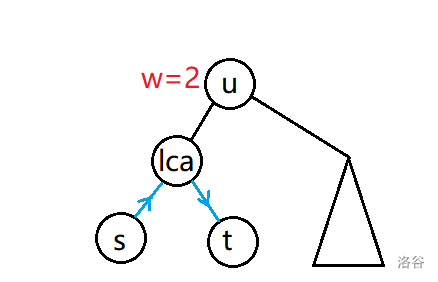
蓝色是应该走的路径,\(u\) 是一点。
按照我们的算法,发现在 \(w=2\) 的观察者 \(u\) 处,点 \(s\) 也符合我们推的式子,但是蓝色路径是不经过 \(u\) 的。这样就产生了多余的答案。解决方法很简单。当归回经过 lca 时,在平衡树上删去 vector 里的数值,就可以取消在 lca 上方 \(s\) 的影响。
由此其实可以发现,这里叫做差分其实是不妥当的,不如称其为修正(然而我代码里仍然写的是差分qwq)。
以上我们便完成了上行的计算。下行的计算是类似的,只是把存进平衡树和 vector 的 \(d_s\) 改为 \(d_t-dis\), 归回时询问 \(d_u-w_u\) 的数量即可。记得初始化平衡树和 vector.
还有,当 \(d_{lca}+w_{lca}=d_s\) 时,\(s\) 和 \(lc\) 同时符合两个式子,会被计算两次,因此应预先减去一次。如果样例第一个输出了4就是这种情况。
代码:
#include <iostream>
#include <vector>
#include <random>
#include <cstring>
#define maxn 310000
using namespace std;
int n,m;
int rt[maxn];//平衡树森林
int w[maxn];
int dis[maxn];//路径长度
int s[maxn],t[maxn];
int lc[maxn];//每条路径的lca
vector<int> chafen[maxn];//那个vector数组
int d[maxn];//节点深度
int ans_[maxn];//每个节点的答案
struct node{//我写的treap啦
int val;
int pri;
int ct;
int ls;
int rs;
int size;
};
vector<node> tree;
struct edge{
int next;
int b;
}e[2*maxn];
int head[maxn];int tot;
void add(int a, int b)
{
e[++tot].b=b;
e[tot].next=head[a];
head[a]=tot;
}
int ac[maxn][30];
std::mt19937 getpri;
int newnode(int val)
{
int pri=getpri();
tree.push_back(node{val,pri,1,0,0,1});
return tree.size()-1;
}
void pushup(int u)
{
tree[u].size=tree[tree[u].ls].size+tree[tree[u].rs].size+tree[u].ct;
}
void rotate_l(int &u)
{
int v=tree[u].rs;
tree[u].rs=tree[v].ls;
tree[v].ls=u;
tree[v].size=tree[u].size;
pushup(u);
u=v;
}
void rotate_r(int &u)
{
int v=tree[u].ls;
tree[u].ls=tree[v].rs;
tree[v].rs=u;
tree[v].size=tree[u].size;
pushup(u);
u=v;
}
void insert(int &u, int val)
{
if(u==0)
{
u=newnode(val);
return;
}
tree[u].size++;
if(tree[u].val==val)
{
tree[u].ct++;
//tree[u].size++;
return;
}
if(tree[u].val<val)
{
int tmp=tree[u].rs;
insert(tmp,val);
tree[u].rs=tmp;
if(tree[tree[u].rs].pri<tree[u].pri)
rotate_l(u);
}else{
int tmp=tree[u].ls;
insert(tmp,val);
tree[u].ls=tmp;
if(tree[tree[u].ls].pri<tree[u].pri)
rotate_r(u);
}
}
bool remove(int &u, int val)
{
if(u==0)return 0;
bool flag;
if(tree[u].val==val)
{
if(tree[u].ct>1)
{
tree[u].ct--;
tree[u].size--;
return 1;
}
if(tree[u].ls==0||tree[u].rs==0)
{
u=tree[u].ls+tree[u].rs;
return 1;
}else if(tree[tree[u].ls].pri<tree[tree[u].rs].pri){
rotate_r(u);
return remove(u,val);
}else{
rotate_l(u);
return remove(u,val);
}
}else if(tree[u].val<val)
{
flag=remove(tree[u].rs,val);
if(flag)tree[u].size--;
}else{
flag=remove(tree[u].ls,val);
if(flag)tree[u].size--;
}
return flag;
}
int getcount(int u, int val)//特别的函数,得到某一个数值的出现次数
{
if(u==0)return 0;
if(val==tree[u].val)
{
return tree[u].ct;
}
if(val<tree[u].val)
{
return getcount(tree[u].ls,val);
}else {
return getcount(tree[u].rs,val);
}
}
int getk(int u, int k)
{
if(u==0)return 0;
if(k<=tree[tree[u].ls].size)
{
return getk(tree[u].ls, k);
}else if(k>tree[tree[u].ls].size+tree[u].ct){
return getk(tree[u].rs,k-tree[tree[u].ls].size-tree[u].ct);
}else{
return tree[u].val;
}
}
inline int read()
{
register char ch=getchar();
register int x=0,cf=1;
while(ch<'0'||ch>'9') {if(ch=='-') cf=-1;ch=getchar();}
while(ch>='0'&&ch<='9') {x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
return x*cf;
}
inline void out(int a)
{
if(a>=10)out(a/10);
putchar(a%10+'0');
}
void dfs1(int u, int fa)
{
d[u]=d[fa]+1;
ac[u][0]=fa;
for(int i = 1; i < 25; i++)
ac[u][i]=ac[ac[u][i-1]][i-1];
for(int i = head[u]; i; i=e[i].next)
{
int v=e[i].b;
if(v!=fa)dfs1(v,u);
}
}
int lca(int u, int v)
{
if(d[u]<d[v])
swap(u,v);
for(int i = 25; i >= 0; i--)
{
if(d[ac[u][i]]>=d[v])
u=ac[u][i];
}
if(u==v)return u;
for(int i = 25; i >= 0; i--)
{
if(ac[u][i]!=ac[v][i])
{
u=ac[u][i];
v=ac[v][i];
}
}
return ac[v][0];
}
void merge(int &a, int &b)//把b合并到a
{
if(a==0||b==0)
{
a=a+b;return;
}
if(tree[a].size>=tree[b].size)
{
while(tree[b].size)
{
int tar=getk(b,1);
remove(b,tar);
insert(a,tar);
}
}else{
while(tree[a].size)
{
int tar=getk(a,1);
remove(a,tar);
insert(b,tar);
}
a=b;
}
}
void dfs2(int u, int fa)
{
for(int i = head[u]; i; i=e[i].next)
{
int v=e[i].b;
if(v==fa)continue;
dfs2(v,u);
merge(rt[u],rt[e[i].b]);//合并子树信息
}
ans_[u]+=getcount(rt[u],w[u]+d[u]);//计算答案
for(int i = 0; i < chafen[u].size(); i++)
{
remove(rt[u],chafen[u][i]);//移除多余信息(或者按照别人的叫法,差分)
}
}//其实dfs2和dfs3就是我前面说的,分别计算上行和下行的两遍dfs
void dfs3(int u, int fa)
{
for(int i = head[u]; i; i=e[i].next)
{
int v=e[i].b;
if(v==fa)continue;
dfs3(v,u);
merge(rt[u],rt[e[i].b]);
}
ans_[u]+=getcount(rt[u],-w[u]+d[u]);
for(int i = 0; i < chafen[u].size(); i++)
{
remove(rt[u],chafen[u][i]);
}
}
int main()
{
cin >> n >> m;
tree.push_back({0,0,0,0,0,0});
for(int i = 1; i < n; i++)
{
int u, v;
u=read();v=read();
add(u,v);add(v,u);
}
for(int i = 1; i <= n; i++)
{
w[i]=read();
}
dfs1(1,0);
for(int i = 1; i <= m; i++)
{
s[i]=read();t[i]=read();
//cout << "Yaolaili"<<endl;
lc[i]=lca(s[i],t[i]);
insert(rt[s[i]],d[s[i]]);
chafen[lc[i]].push_back(d[s[i]]);
dis[i]=d[s[i]]+d[t[i]]-d[lc[i]]*2;
if(d[lc[i]]+w[lc[i]]==d[s[i]])ans_[lc[i]]--;
}
dfs2(1,0);
tree.clear();
memset(rt,0,sizeof(rt));
tree.push_back({0,0,0,0,0,0});
for(int i = 1; i <= n; i++)
{
chafen[i].clear();
}
for(int i = 1; i <= m; i++)
{
insert(rt[t[i]],d[t[i]]-dis[i]);
chafen[lc[i]].push_back(d[t[i]]-dis[i]);
}
dfs3(1,0);
for(int i = 1; i <= n; i++)
{
out(ans_[i]);putchar(' ');
}
}
实现细节
对于平衡树森林,我们其实不需要开 tree 数组,只需要开 rt 数组即可,记录每一颗平衡树的根。
lg同号,非抄
标签:ac,int,题解,tree,Treap,maxn,lca,P1600,size 来源: https://www.cnblogs.com/the-bjxs-blog/p/16504306.html