[SDOI2013]费用流

题目传送门 洛谷P3305 [SDOI2013]费用流

题目描述

Alice和Bob在图论课程上学习了最大流和最小费用最大流的相关知识。 最大流问题：给定一张有向图表示运输网络，一个源点S和一个汇点T，每条边都有最大流量。

一个合法的网络流方案必须满足：

(1)每条边的实际流量都不超过其最大流量且非负；

(2)除了源点S和汇点T之外，对于其余所有点，都满足该点总流入流量等于该点总流出流量；而S点的净流出流量等于T点的净流入流量，这个值也即该网络流方案的总运输量。

最大流问题就是对于给定的运输网络，求总运输量最大的网络流方案。

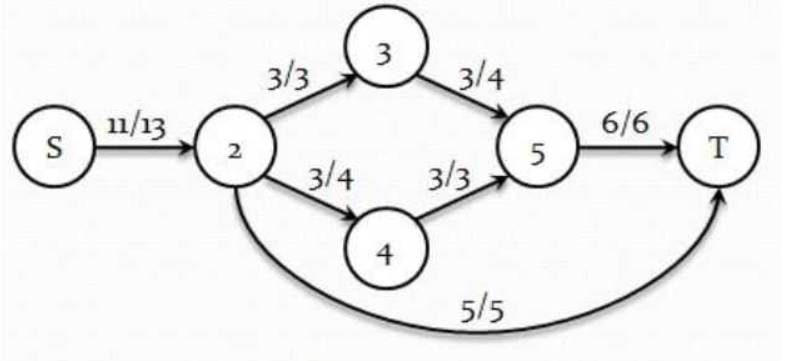
上图表示了一个最大流问题。对于每条边，右边的数代表该边的最大流量，左边的数代表在最优解中，该边的实际流量。需要注意到，一个最大流问题的解可能不是唯一的。

对于一张给定的运输网络，Alice先确定一个最大流，如果有多种解，Alice可以任选一种；之后Bob在每条边上分配单位花费（单位花费必须是非负实数），要求所有边的单位花费之和等于P。

总费用等于每一条边的实际流量乘以该边的单位花费。需要注意到，Bob在分配单位花费之前，已经知道Alice所给出的最大流方案。现茌Alice希望总费用尽量小，而Bob希望总费用尽量大。我们想知道，如果两个人都执行最优策略，最大流的值和总费用分别为多少。

输入格式

第一行三个整数N，M，P。N表示给定运输网络中节点的数量，M表示有向边的数量，P的含义见问题描述部分。为了简化问题，我们假设源点S是点1，汇点T是点N。

接下来M行，每行三个整数A，B，C，表示有一条从点A到点B的有向边，其最大流量是C。

输出格式

第一行一个整数，表示最大流的值。第二行一个实数，表示总费用。建议选手输出四位以上小数。

样例 #1

样例输入 #1

3 2 1
1 2 10
2 3 15

样例输出 #1

10
10.0000

提示

【样例说明】

对于Alice，最大流的方案是固定的。两条边的实际流量都为10。

对于Bob，给第一条边分配0.5的费用，第二条边分配0.5的费用。总费用为：10*0.5+10*0.5=10。可以证明不存在总费用更大的分配方案。

【数据规模和约定】

对于20%的测试数据：所有有向边的最大流量都是1。

对于100%的测试数据：N < = 100，M < = 1000。

对于l00%的测试数据：所有点的编号在I..N范围内。1 < = 每条边的最大流量 < = 50000。1 < = P < = 10。给定运输网络中不会有起点和终点相同的边。

思路

blabla..
先自己看着猜
要是猜不到

代码实现

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
double temp;

const int N=400100,M=400100,inf=1e8;
const double eps=1e-8;   
double f[M];
int tt,S,T,n,m,p;
int e[M],ne[M];
int q[N],cur[N],h[N],d[N],idx;
int u[5050],v[5050];
double cc[2020];
void add(int a,int b,double c)
{
	e[idx]=b,f[idx]=c,ne[idx]=h[a],h[a]=idx++;
	e[idx]=a,f[idx]=0,ne[idx]=h[b],h[b]=idx++;
}

inline bool bfs()
	{
		int tt=0,hh=0;
		memset(d,-1,sizeof d);
		q[0]=S,d[S]=0,cur[S]=h[S];
		while(hh<=tt)
		{
			int t=q[hh++];
			for(int i=h[t];~i;i=ne[i])
			{
				int ver=e[i];
				if(d[ver]==-1&&f[i]>eps)
				{
					d[ver]=d[t]+1;
					cur[ver]=h[ver];
					if(ver==T) return true;
					q[++tt]=ver;
				}
			}
		}
		return false;
	}	
inline double find(int u,double limit)
	{
		if(u==T) return limit;
		double flow=0;
		
		for(int i=cur[u];~i&&eps<limit-flow;i=ne[i])
		{
			int ver=e[i];
			cur[u]=i;
			if(d[ver]==d[u]+1&&f[i]>eps)
			{
				double t=find(ver,min(limit-flow,f[i]));
				if(t<eps) d[ver]=-1;
				f[i]-=t;
				f[i^1]+=t;
				flow+=t;	
			}
			
		}
		return flow;
	}
	
inline double dinic()
{
	double ans=0,flow;
	while(bfs())
	{
		while(flow=find(S,inf)) ans+=flow;
	}
	return ans;
}


inline bool check(double mid)
{
	
	idx=0;
	memset(h,-1,sizeof h);
	for(int i=1;i<=m;i++)
	{
		//f[i]=min(f[i],mid);
		add(u[i],v[i],min(cc[i],mid));
	}

	return fabs(dinic()-temp)<eps;
}

int main()
{
	cin>>n>>m>>p;
	S=1,T=n;
	memset(h,-1,sizeof h);
	double tt=-1.0;
	for(int i=1;i<=m;i++)
	{
	
	    cin>>u[i]>>v[i]>>cc[i];
		add(u[i],v[i],cc[i]);
		if(tt<cc[i])tt=cc[i];
	}
	temp=dinic();
	printf("%.0f\n",temp);
	
    double l=0,r=(double)tt;
    while (r-l>eps)
    {
        double mid=(l+r)/2.0;
        if (check(mid)) r=mid;
        else l=mid;
     //   cout<<l<<" "<<r<<endl;
    }
    printf("%.4f",l*(double)p);
  
	return 0;
}                

标签：费用,最大,idx,10,int,题解,流量,SDOI2013,double
来源： https://www.cnblogs.com/watasky/p/16483509.html