[Note]Catalan数学习笔记

浅探 Catalan 数

Catalan 数是一种常见于数列OI的一种组合数。

几个基本模型：

1. \(n\) 个 \(+1\) ， \(n\) 个 \(-1\) 构成一个序列，要求序列的任意前缀和非负。（好用的理解）
2. 在平面直角坐标系 \(xOy\) 种，每次可以沿着 \(y\) 轴正半轴或 \(x\) 轴负半轴移动一格，不越过直线 \(y=x\) 的到达 \((n,n)\) 的总方案数。（易拓展的理解）

这里对模型 \(2\) 进行一定的讲解：

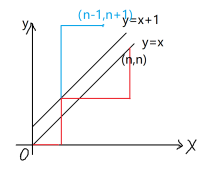
正难则反，我们可以通过不考虑限制到达 \((n,n)\) 的方案数减去不合法的方案数，这也便是 \(\operatorname{Catalan}_n\) （下面使用 \(h_n\) 表示）的计算式。

那不合法的方案数如何计算呢？

一个简单但重要的结论：如果它不合法，那么它必定经过直线 \(y=x+1\)。

那么我们将路径与 \(y=x+1\) 的第一个交点以后的部分翻转，那么就可以发现，所有不合法的路径都可以转化成从原点到 \((n-1,n+1)\) 的一条路径（必要性和充分性的证明容易从上面的结论得出）。

所以我们就可以得出路径数量为 \(C_{2\times n}^{n} - C_{2\times n}^{n+1}\)。

一个常用的结论

容易发现在 Catalan 数的应用中很容易遇到关于一个点关于直线 \(y=x+b\) 对称的问题，以下给出结论（方便运用）：

\((X,Y)\rightarrow (Y+b,X-b)\)

Catalan 数的几个简单计算式

1. \(C_{2\times n}^{n} - C_{2\times n}^{n+1}\)
2. \(\dfrac{C_{2\times n}^{n}}{n+1}\) （注：\(C_{2\times n}^{n+1}=\dfrac{n}{n+1}\times C_{2\times n}^{n}\)）
3. 同时也易得递推式：\(h_i=h_{i-1}\times \dfrac{4n-2}{n+1}\)
4. \(h_n=\sum_{i=0}^{n-1} h_i\times h_{n-i-1}\) （不同 \(n\) 个节点的二叉树个数模型）

咕咕咕咕

标签：结论,dfrac,路径,笔记,times,Note,Catalan,合法
来源： https://www.cnblogs.com/1l2u3o/p/16483098.html