首页 > 其他分享> > 使用树状数组优化LIS问题

使用树状数组优化LIS问题

2022-07-11 12:10:34 作者：互联网

使用树状数组优化\(LIS\)问题

一、与贪心+二分的方法对比

树状数组可以用来优化\(LIS\)问题,与贪心+二分的优化方式相比

优点：

二分作法只能计算出当前序列的\(LIS\),而树状数组可以计算出以每一个\(a(i)\)为结尾的\(LIS_i\)。(随进随查,不能算完一起来查)
学会了树状数组优化\(LIS\)后，后面有一道求最长上升序列和的问题，也可以使用树状数组优化为\(O(nlogn)\)，而贪心+二分则无法优化那道题。

缺点:

同样是\(O(nlogn)\)的复杂度，树状数组的常数更大，贪心+二分的常数更小。可以通过\(AcWing 896\)的提交日志查看到结果对比，当然，你也可以说是此网站的数据问题，但有一定的代表性：

贪心+二分	树状数组(静态)	树状数组(动态)
\(194\) \(ms\)	\(580\) \(ms\)	\(851\) \(ms\)

贪心+二分的做法能计算出答案，想要获得具体方案则需要通过其它辅助办法记录路径。树状数组如果想要获得路径，也需要配合辅助数据进行计算(~~这个我没实验过~~)。

二、树状数组是怎么优化问题的？

树状数组只是一个优化，本质上还是原始的\(O(n^2)\)动态规划求\(LIS\)，解决的是在递推时计算\(f[i]\)时，优化了

for(int j=1;j<i;j++)
  if(a[i]>a[j]) f[i]=max(f[i],f[j]+1)

因为这就是一个暴力的枚举过程，所以造成了\(O(n^2)\)的时间复杂度，现在想要找一个办法，将此处的寻找能接、可接的\(f[i]\)进行优化。

问题描述

我\(a[i]\)前面的
值比我小的:\(a[j]<a[i]\)
最大那个
我要接在它的后面 \(f[j]+1\)

解决办法

我\(a[i]\)前面的
- for(i=0;i<n;i++)保证每个\(a[i]\)讨论时，都只关心它前面的计算结果。
值比我小的:\(a[j]<a[i]\)
- 这个需要转化一下：复制数组进行排序+离散化，可以知道当前要处理的数字\(a[i]\)的排名，我只关心排名比我小的信息。
最大的那个
- 采用的是用树状数组维护从开头到排名的最大值。树状数组本质上是一个数据结构：
  - 对外提供：快速查询到目前为止，排名\(k\)位的\(LIS[k]=query(k)\)。
    
    注意:动态录入+动态获取!
    随着更多数据的录入，查询结果会变化，不能最终一并查询，只能是边录边查！
  - 内部实现：以二进制形式分块保存的统计数据，以本题而言，就是分块保存的范围内最大值，此最大值，并不能直接使用，对外提供查询功能时，需要枚举所有前序分块，汇总最大值。

举个栗子：

7
3 1 2 1 8 5 6

通过排序加去重，给每个数字都标识了它在原序列中排名是多少：

排序+去重数组\(b[]\)

下标	\(0\)	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)
排名	\(1\)	\(2\)	\(3\)	\(4\)	\(5\)	\(6\)
数值	\(1\)	\(2\)	\(3\)	\(5\)	\(6\)	\(8\)

整出来个\(b[]\)数组有啥用呢？就是为了知道当前要操作的数字\(a[i]\)它的排名是多少，根据它的排名，可以知道它的前一名，查询到前一名时的最大\(LIS\)值，我接在它后面\(+1\)就是答案。

配合下面的树状数组结构图以便深入理解：

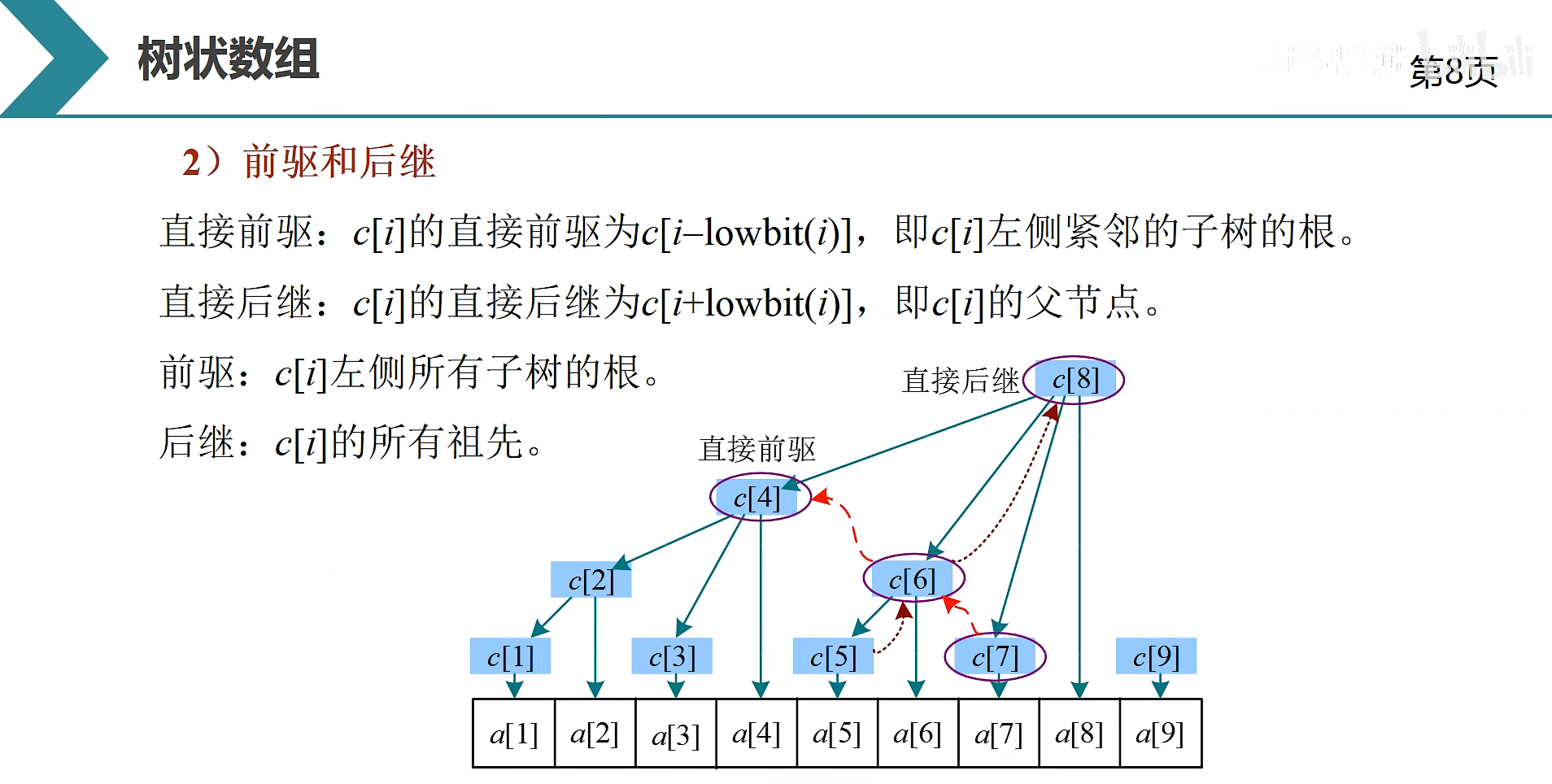
编写一个带调试信息的代码，输出调试信息，方便理解

\[talk　 is　 cheap,show　me　 your　 code! \]

#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x & -x)
const int N = 1e5 + 10;

int n, a[N];
int b[N], bl; //离散化数组，用于辅助树状数组
int c[N];     //树状数组
int res;      //结果

//计算x值在原序列中的排名
int get(int x) {
    return lower_bound(b, b + bl, x) - b + 1;
}

//单点更新x
void update(int i, int x) {
    for (; i <= bl; i += lowbit(i)) c[i] = max(c[i], x);
}

//求1~i的最大值
int query(int i) {
    int s = 0;
    for (; i; i -= lowbit(i)) s = max(s, c[i]);
    return s;
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d", &a[i]), b[i] = a[i];

    //离散化，用于获取 x值->排名k 的关系
    sort(b, b + n);
    // bl：去重后的长度
    bl = unique(b, b + n) - b;
    /*
    测试用例：
    7
    3 1 2 1 8 5 6
    */
    for (int i = 0; i < n; i++) {
        puts("==============================================");
        printf("i:%d a[i]=%d\n", i, a[i]);
        int k = get(a[i]); // a[i]的排名k
        printf("rank:%d rank-1:%d\n", k, k - 1);
        int t = query(k - 1) + 1;
        printf("LIS[rank-1]:%d ", t - 1);
        printf("LIS[rank]:%d\n", t);
        res = max(res, t);
        update(k, t); //第k大的数，会接在第k-1大的数后面，才会获取到更大的连续LIS值
        puts("FenWickTree:");
        for (int i = 1; i <= bl; i++) printf("%d ", c[i]);
        puts("");
    }
    return 0;
}

输出的结果：

==============================================
i:0 a[i]=3
rank:3 rank-1:2
LIS[rank-1]:0 LIS[rank]:1
FenWickTree:
0 0 1 1 0 0
==============================================
i:1 a[i]=1
rank:1 rank-1:0
LIS[rank-1]:0 LIS[rank]:1
FenWickTree:
1 1 1 1 0 0
==============================================
i:2 a[i]=2
rank:2 rank-1:1
LIS[rank-1]:1 LIS[rank]:2
FenWickTree:
1 2 1 2 0 0
==============================================
i:3 a[i]=1
rank:1 rank-1:0
LIS[rank-1]:0 LIS[rank]:1
FenWickTree:
1 2 1 2 0 0
==============================================
i:4 a[i]=8
rank:6 rank-1:5
LIS[rank-1]:2 LIS[rank]:3
FenWickTree:
1 2 1 2 0 3
==============================================
i:5 a[i]=5
rank:4 rank-1:3
LIS[rank-1]:2 LIS[rank]:3
FenWickTree:
1 2 1 3 0 3
==============================================
i:6 a[i]=6
rank:5 rank-1:4
LIS[rank-1]:3 LIS[rank]:4
FenWickTree:
1 2 1 3 4 4
==============================================

理解一下代码的执行流程

i:0 a[i]=3
rank:3 rank-1:2
LIS[rank-1]:0 LIS[rank]:1
FenWickTree:
0 0 1 1 0 0

\(3\)开始,查询到排名是\(3\),查询前一个排名的\(LIS[2]=query(2)\)，第一个嘛，前面没有，所以是\(0\),把它的排名在前序排名上面加\(1\),记\(c[3]=1\),含义为本片片长\(c[3]\)知道自己管辖范围内(\(a[3]\))的最长上升子序列长度为\(1\)。同时，向各级领导汇报，告诉\(c[4]\),你的孩子\(c[3]\)目前\(LIS\)是\(1\),你们看看用不用更新一下自己的最大值。如果此时要查询排名\(3\)以下的最长上升子序列长度值，就是执行\(query(3)\),代码会去找\(c[3]\)和\(c[2]\),\(pk\)大小后返回较大值。

i:1 a[i]=1
rank:1 rank-1:0
LIS[rank-1]:0 LIS[rank]:1
FenWickTree:
1 1 1 1 0 0

\(1\)开始,查询到排名是\(1\)，查询前一个排名的\(LIS[0]=query(0)=0\)，标识\(c[1]=1\),同时也要向上尝试\(PK\)更新\(c[2],c[4]\),结果\(c[2]\)被修改为\(1\)。

i:2 a[i]=2
rank:2 rank-1:1
LIS[rank-1]:1 LIS[rank]:2
FenWickTree:
1 2 1 2 0 0

\(2\)开始，查询到排名是\(2\),查询前一个排名的\(LIS[1]=query(1)\),知道前面最大值是\(1\),则\(c[2]=2\),同时更新\(c[4]=2\)

i:3 a[i]=1
rank:1 rank-1:0
LIS[rank-1]:0 LIS[rank]:1
FenWickTree:
1 2 1 2 0 0

\(1\)开始，查询到排名是\(1\),查询前一个排名的\(LIS[0]=query(0)=0\),将\(c[1]\)尝试修改为\(1\),并尝试更新\(c[2],c[4]\),当然，现在更新不了，人家原来的就比\(1\)大。

i:4 a[i]=8
rank:6 rank-1:5
LIS[rank-1]:2 LIS[rank]:3
FenWickTree:
1 2 1 2 0 3

\(8\)开始，查询到排名是\(6\),查询前一个排名的\(LIS[5]=query(5)\),此时\(c[5]=0\),则\(max(c[5],c[4])=2\),表示现在排名前\(5\)位之前的\(LIS=2\),所以\(c[6]=2+1=3\)。

i:5 a[i]=5
rank:4 rank-1:3
LIS[rank-1]:2 LIS[rank]:3
FenWickTree:
1 2 1 3 0 3

\(5\)开始，查询到排名是\(4\),查询前一个排名的\(LIS[3]=query(3)=max(c[3],c[2])=2\),则\(c[4]=2+1=3\)

i:6 a[i]=6
rank:5 rank-1:4
LIS[rank-1]:3 LIS[rank]:4
FenWickTree:
1 2 1 3 4 4

\(6\)开始，查询到排名是\(5\),查询前一个排名的\(LIS[4]=query(4)==c[4]=3\),则\(c[5]=3+1=4\)

三、树状数组实现代码1

//运行时间： 601 ms
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x & -x)
const int N = 1e5 + 10;

int n, a[N];
int b[N], bl; //离散化数组，用于辅助树状数组
int tr[N];    //树状数组
int res;      //结果

//计算x值在原序列中的排名
int get(int x) {
    return lower_bound(b, b + bl, x) - b + 1;
}

//单点更新x
void update(int i, int x) {
    for (; i <= bl; i += lowbit(i)) tr[i] = max(tr[i], x);
}

//求tr[1]~tr[i]的最大值
int query(int i) {
    int s = 0;
    for (; i; i -= lowbit(i)) s = max(s, tr[i]);
    return s;
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d", &a[i]), b[i] = a[i];

    //离散化，用于获取 x值->排名k 的关系
    sort(b, b + n);
    // bl：去重后的长度
    bl = unique(b, b + n) - b;

    for (int i = 0; i < n; i++) {
        int k = get(a[i]); //值a[i]的排名k
        int t = query(k - 1) + 1;
        res = max(res, t);
        update(k, t); //第k大的数，会接在第k-1大的数后面，才会获取到更大的连续LIS值
    }
    //输出
    printf("%d\n", res);
    return 0;
}

四、树状数组实现代码2

//运行时间： 582 ms
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x & -x)
const int N = 1e5 + 10;

int n, a[N];
int b[N], bl; //离散化数组，用于辅助树状数组
int tr[N];    //树状数组
int res;      //结果

//计算x值在原序列中的排名
int get(int x) {
    return lower_bound(b, b + bl, x) - b + 1;
}

//单点更新x
void update(int i, int x) {
    for (; i <= bl; i += lowbit(i)) tr[i] = max(tr[i], x);
}

//求tr[1]~tr[i]的最大值
int query(int i) {
    int s = 0;
    for (; i; i -= lowbit(i)) s = max(s, tr[i]);
    return s;
}

int main() {
    scanf("%d", &n);
    for (int i = 0; i < n; i++) scanf("%d", &a[i]), b[i] = a[i];

    //离散化，用于获取 x值->排名k 的关系
    sort(b, b + n);
    // bl：去重后的长度
    bl = unique(b, b + n) - b;

    for (int i = 0; i < n; i++) {
        int k = get(a[i]); //值a[i]的排名k
        int t = query(k - 1) + 1;
        update(k, t); //第k大的数，会接在第k-1大的数后面，才会获取到更大的连续LIS值
    }
    //输出
    printf("%d\n", query(bl));
    return 0;
}

五、树状数组实现代码3

//运行时间： 863 ms
#include <bits/stdc++.h>
using namespace std;
#define lowbit(x) (x & -x)
const int N = 1e5 + 10;

int n, a[N];
//树状数组
int tr[N];
//离散化数组，提供指定值对应的排名,辅助树状数组
vector<int> b;
int res; //结果

//计算x值在原序列中的排名
int get(int x) {
    return lower_bound(b.begin(), b.end(), x) - b.begin() + 1;
}

//求tr[1]~tr[i]的最大值
int query(int i) {
    int s = 0;
    for (; i; i -= lowbit(i)) s = max(s, tr[i]);
    return s;
}

//单点更新x
void update(int i, int x) {
    for (; i <= n; i += lowbit(i)) tr[i] = max(tr[i], x); //注意这里是跳着取max,不是传统的sum求和
}

int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i]);
        b.push_back(a[i]);
    }

    //离散化,用于存储a数组按值由小到大去重排序的结果，这样就可以使用二分查找  值->排名
    sort(b.begin(), b.end());
    b.erase(unique(b.begin(), b.end()), b.end());

    for (int i = 1; i <= n; i++) { //按原输入序进行遍历，这样才符合LIS的要求
        int k = get(a[i]);         //获取值a[i]的整体大小排名k
        int t = query(k - 1) + 1;  //在树状数组中查找排名为k-1的最大数量，再加1才是当前连接上后的数量
        update(k, t);              //将排名k更新目前最优解t
    }
    //输出
    printf("%d\n", query(b.size()));
    return 0;
}

六、总结与感悟

树状数组用于快速查询\(O(logN)\)前缀和，区间和，区间\([1\sim i]\)的最大值。
树状数组强调的是　一边修改一边查询的场景，纯静态的、离线查询的，不如原始前缀和。
树状数组中保存的数据，是具有片断性的， 不能直接拿来用，要现用现组装。(不要和我犟说\(c[4],c[8]\)就不用组装之类的话~)
树状数组能做的事：单点修改，可使用减法原则的区间查询，对于区间修改请移步线段树。
相对线段树，代码量少。

标签：树状,int,rank,数组,LIS,排名
来源： https://www.cnblogs.com/littlehb/p/16465901.html