首页 > 其他分享> > 树的直径与重心学习笔记

树的直径与重心学习笔记

2022-07-10 13:00:09 作者：互联网

树的直径

定义

在一棵树上（默认无根树），定义 \(\operatorname{Dis}(u,v)\) 表示 \(u\) 到 \(v\) 的最短路径。

树的直径就是 \(\max\{\operatorname{Dis}\}\)。

求法

一般使用两遍DFS打法。（当然，也可以使用树上DP）

首先，任意选一个点 \(w\)，从这个点出发，DFS整棵树，然后预处理 \(\operatorname{Deep}\)。

再找出最深的一个点 \(u\)，然后从这个点出发，DFS整棵树，然后覆盖深度 \(\operatorname{Deep}\)。

这时找出深度最大的点 \(v\)， \(\operatorname{Dis}(u,v)\)（也就是 \(\operatorname{Deep}(v)\) ）就是该树的直径。

整体时间复杂度 \(O(n)\)，需要 \(O(n)\) 的辅助空间。

SPPT07Z - Longest path in a tree

题目描述

给你一个无权无向的树。编写程序以输出该树中最长路径（从一个节点到另一个节点）的长度。在这种情况下，路径的长度是我们从开始到目的地的遍历边数。

输入格式

输入文件的第一行包含一个整数 \(N\)——树中的节点数。接下来 \(N-1\)行包含该树的 \(N-1\) 个边---每行包含一对 \((u,v)\)，表示在节点 \(u\) 和节点 \(v\) 之间存在边。

输出格式

输出最长路径的长度。

思路

树的直径模板题。

代码

#include <bits/stdc++.h>
using namespace std;

struct edge{
    int nxt,to,w;
} tree[114514<<1];
int head[114514],ec;
void add(int from,int to,int weight){
    tree[++ec].nxt=head[from];
    tree[ec].to=to;
    tree[ec].w=weight;
    head[from]=ec;
}

int n;

int deep[114514],deepmax=0;
void dfs(int now,int parent){
    deep[now]=deep[parent]+1;
    if(deep[now]>deep[deepmax]){
    	deepmax=now;
	}
    for(int i=head[now];i;i=tree[i].nxt){
        if(tree[i].to != parent){
            dfs(tree[i].to,now);
        }
    }
}

int main(){
	cin>>n;
	for(int i=1,u,v;i<n;i++){
		cin>>u>>v;
		add(u,v,114);
		add(v,u,514);
	}	
	deep[0]=-1;
	dfs(1,0);
	dfs(deepmax,0);
	cout<<deep[deepmax]<<'\n';
	return 0;
}

Record on SPOJ

Record on Luogu

树的重心

定义

对于树上的每一个点，计算其所有子树中最大的子树节点数，这个值最小的点就是这棵树的重心。注意树的重心可能有多个。（来源：树的重心 - OI Wiki）

一般来说，我们只需要记住这个性质就行了：

树上所有的点到树的重心的距离之和是最短的，如果有多个重心，那么总距离相等。(来源：题解 P1364 【医院设置】 - Qihoo360 的博客 - 洛谷博客）

求法

最短路法

基本思路：跑一遍最短路，然后暴力找最短路径和最小的点。

可以使用以下算法

Floyd(\(O(n^3)\)）
Dijkstra（本问题 \(O(n^3)\)）
堆优化Dijkstra(本问题 \(O(n^3\log n)\)）
SPFA（本问题 \(O(n^{3})\)）
Johnson 全源最短路算法（本问题 \(O(n^3\log n)\)）

因此，这种算法大致时间复杂度为 \(O(n^{3})\)。

LCA法

我们不必用 \(O(n^3)\) 的时间复杂度求出所有点之间的距离。还记得 LCA吗？

树上两个点的距离为：

\[\operatorname{Dis}(u,v)= \operatorname{Deep}(u)+\operatorname{Deep}(v)- 2\times \operatorname{Deep}(\operatorname{LCA}(u,v)) \]

所以我们可以用倍增来求出LCA，然后统计。时间复杂度 \(O(n^{2}\log n)\)（我不知道为什么那么多人说是 \(O(n^2)\) 的）

P1364 医院设置

题目描述

设有一棵二叉树，如图：

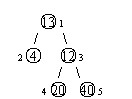
其中，圈中的数字表示结点中居民的人口。圈边上数字表示结点编号，现在要求在某个结点上建立一个医院，使所有居民所走的路程之和为最小，同时约定，相邻接点之间的距离为 \(1\)。如上图中，若医院建在1 处，则距离和 \(=4+12+2\times20+2\times40=136\)；若医院建在 \(3\) 处，则距离和 \(=4\times2+13+20+40=81\)。

输入格式

第一行一个整数 \(n\)，表示树的结点数。

接下来的 \(n\) 行每行描述了一个结点的状况，包含三个整数 \(w, u, v\)，其中 \(w\) 为居民人口数，\(u\) 为左链接（为 \(0\) 表示无链接），\(v\) 为右链接（为 \(0\) 表示无链接）。

输出格式

一个整数，表示最小距离和。

数据规模与约定

对于 \(100\%\) 的数据，保证 \(1 \leq n \leq 100\)，\(0 \leq u, v \leq n\)，\(1 \leq w \leq 10^5\)。

思路

其实就是求一棵二叉树的重心，然后再 \(O(n)\) 统计答案。

数据量较小，可以Floyd，时间复杂度 \(O(n^3)\)。

代码

#include <bits/stdc++.h>
#define OLLO_AK_IOI(arr) memset(arr,0x3f,sizeof(arr))
using namespace std;

int f[114][514],a[114];
int n,ans=INT_MAX;

int main(){
	OLLO_AK_IOI(f);
	cin>>n;
	for(int i=1,u,v;i<=n;i++){
		f[i][i]=0;
		cin>>a[i]>>u>>v;
		if(u!=0){
			f[i][u]=1;
			f[u][i]=1;
		}
		if(v!=0){
			f[i][v]=1;
			f[v][i]=1;
		}
	}
	for(int k=1;k<=n;k++){
		for(int i=1;i<=n;i++){
			for(int j=1;j<=n;j++){
				f[i][j]=min(f[i][j],f[i][k]+f[k][j]);	
			}
		}
	}
	for(int hospital=1;hospital<=n;hospital++){
		int sum=0;
		for(int i=1;i<=n;i++){
			sum+=(f[hospital][i])*a[i];
		}
		ans=min(sum,ans);
	}
	cout<<ans<<'\n';
	return 0;
}

Record on Luogu

标签：重心,int,复杂度,笔记,leq,Deep,直径,operatorname
来源： https://www.cnblogs.com/zheyuanxie/p/tree-diameter-centroid.html