其他分享
首页 > 其他分享> > 网络流练习

网络流练习

作者：互联网

目录

网络流练习

若是一个点经过的次数有限制，则需要拆点

拆点的妙用博大精深

注：下文中 \(s\) 指超级源点，\(t\) 指超级汇点

这里是最大流dinic的代码和费用流EK的代码

最大流

P1231 教辅的组成

题意：

现在有 \(a,b,c\) 三种东西，分别有 \(n1,n2,n3\) 个

告诉你 \(m1\) 组 \(a,b\) 的对应关系，\(m2\) 组 \(a,c\) 的对应关系

只有 \(a_i\) 同时对应 \(b_j\) 和 \(c_k\)，\(a_i\) 才能和 \(b_j\) 与 \(c_k\) 配成一套

问在不重复的条件下最多可以配成几套

思路：

很基础的最大流

由于 \(a\) 对应 \(b\) 和 \(c\) ，考虑建图时把所有 \(a\) 放中间 \(b,c\) 放两边

从 \(s\) 向所有 \(b\) 连一条容量为 \(1\) 的边，从所有 \(c\) 向 \(t\) 连一条容量为 \(1\) 的边

从所有 \(b\) 向所有 \(a\) 连一条容量为 \(1\) 的边，从所有 \(a\) 向所有 \(c\) 连一条容量为 \(1\) 的边

跑最大流就行

但是我 \(Wrong\ Answer\) 了 \(QAQ\)

这是因为 \(a\) 在中间，若是像下面一样会算两次：

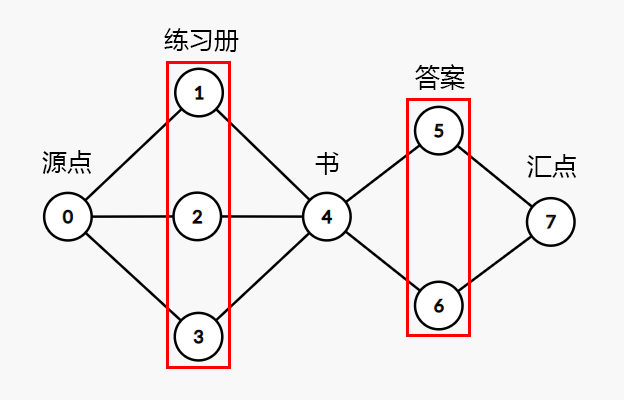
so，我们把中间的所有 \(a\) 拆成两个点，加一条容量为 \(1\) 的边

最大流即为答案

P2472 蜥蜴

题意：

在一个 \(r\) 行 \(c\) 列的网格地图中有一些高度不同的石柱，第 \(i\) 行 \(j\) 列的石柱高度为 \(h_{i,j}\)。

一些石柱上站着一些蜥蜴，你的任务是让尽量多的蜥蜴逃到边界外。

每行每列中相邻石柱的距离为 \(1\)，蜥蜴的跳跃距离是 \(d\)，即蜥蜴可以跳到平面距离不超过 \(d\) 的任何一个石柱上。

石柱都不稳定，每次当蜥蜴跳跃时，所离开的石柱高度减 \(1\)（如果仍然落在地图内部，则到达的石柱高度不变）。

如果该石柱原来高度为 \(1\)，则蜥蜴离开后消失，以后其他蜥蜴不能落脚。

任何时刻不能有两只蜥蜴在同一个石柱上。

思路：

数据范围很小，考虑网络流

因为每个石柱都有经过次数限制，所以要位置 \(i\) 拆成点 \(i\) 和 \(i'\) ，且 \(i\) 和 \(i'\) 之间连一条容量为 \(h_i\) 的边

用 \(i\) 表示跳到了石柱 \(i\)，\(i'\) 表示从 \(i\) 点开始跳向别的石柱

若是能从一个石柱 \(i\) 跳到另一个石柱 \(j\) ，那么就从 \(i'\) 向 \(j\) 连一条容量为 \(inf\) 的边

若是能从一个石柱 \(i\) 跳出边界，那么就从 \(i'\) 向 \(t\) 连一条容量为 \(inf\) 的边

我们可以假设最开始每只蜥蜴都不在石柱上，而是在源点 \(s\)

然后从 \(s\) 向每个蜥蜴初始位置 \(i\) 连一条容量为 \(1\) 的边，表示一只蜥蜴

这样就可以巧妙地解决这个问题

最大流 \(maxflow\) 表示的是最多有多少只蜥蜴能跳走

记录蜥蜴总数 \(sum\)，跑一遍网络流，最终结果为 \(sum-maxflow\)

最小割

P4313 文理分科

题意：

有 \(n\times m\) 个人，每个人要么选文科，要么选理科

第 \(i\) 行 \(j\) 列的人选文科可以获得快乐值 \(art_{i,j}\)，选理科可以获得快乐值 \(sci_{i,j}\)

若是一个人选的文科且上下左右的人都是文科，他可以获得额外快乐值 \(sameart_{i,j}\)

若是一个人选的理科且上下左右的人都是理科，他可以获得额外快乐值 \(samesci_{i,j}\)

求这些人的快乐值总和最大是多少

思路：

非 \(A\) 即 \(B\) ，典型的最小割

先不考虑额外快乐值

在集合 \(S\) 中表示选文科，在集合 \(T\) 中表示选理科

从 \(s\) 向点 \((i,j)\) 连容量为 \(art_{i,j}\) 的边，从点 \((i,j)\) 向 \(t\) 连容量为 \(sci_{i,j}\) 的边

这样求最小割，割掉最少不要的快乐值，剩下的就是答案

考虑额外快乐值

我们新建一个节点 \(x\) 对应点 \((i,j)\) 的文科额外快乐值，从 \(s\) 向点 \(x\) 连容量为 \(sameart_{i,j}\) 的边

考虑上下左右及自己都必须选文科，因此从 \(x\) 向 \((i,j)\)，\((i-1,j)\)，\((i+1,j)\)，\((i,j-1)\)，\((i,j+1)\) 都连一条容量为 \(inf\) 的边

显然这五条边是不会被割掉的

因此若是这五个点中有两个点不在一个集合内，就必须要断掉它们之间的联系，因为 \(x\) 把它们连在一起了

此时不能割容量为 \(inf\) 的边，就只能割容量为 \(sameart_{i,j}\) 的边

理科的同理，我们新建一个节点 \(y\) 对应点 \((i,j)\) 的理科额外快乐值，从 \(y\) 向点 \(t\) 连容量为 \(samesci_{i,j}\) 的边

从 \((i,j)\)，\((i-1,j)\)，\((i+1,j)\)，\((i,j-1)\)，\((i,j+1)\) 向 \(x\) 都连一条容量为 \(inf\) 的边

根据最小割=最大流

跑一边 \(dinic\) 得到最大流 \(maxflow\)，最终的答案是 \(all\_happiness-maxflow\)

P2762 太空飞行计划问题

题意：

给定一张图，有左侧的点和右侧的点，左侧的点点权为正（对应试验），右侧的点点权为负（对应器材），如果选择了左侧的某个点就必须要选右边的一部分点。要求最大化点权和。

思路：

若是左侧的点需要右侧的点，则连一条从左侧的点向右侧的点的有向边，这样问题就转换为：

给定一个有向无环图，点有点权，选择一个子图，满足子图上如果选择了一个点就必须选择它后继的所有点。最大化点权和。

这是一个经典最小割问题，叫做最大权闭合子图问题

建图操作如下：

从 \(s\) 向所有正权值的点连一条权值为点权的边，从所有负权值的店向 \(t\) 连一条权值为点权绝对值的边

保留原图中所有的边且容量为正无穷

则原图中最大点权和为原图中正点权权值和减最小割

\(S\) 包含所有要的点，\(T\) 包含所有不要的点

最小割割去的边必然与 \(s\) 或 \(t\) 相邻，因为其他的边容量均为 \(inf\)

当我们选择要一个正权值点的时候，必然会将其放入集合 \(S\)，这样就会割掉与其相连的负权值点与 \(t\) 的连边，这时候割去了需要减去的值

当我们选择不要一个正权值点的时候，必然会将其放入集合 \(T\)，这样就会割掉其与 \(s\) 相连的边，这时候割去了需要减去的值

这样求得的割就是原图正点权和需要减去的部分，最小割就能减的最少，这样点权和最大

P3227 切糕

题意：

你在切一个蛋糕，蛋糕每个点有一个非负不和谐值 \(v\)，切蛋糕的规则如下：

首先将每一个竖列的坐标用 \((x,y)\) 表示，数列上的点就是 \((x,y,z)\)

每次在每一数列选择一个点

对于数列 \((x,y)\) 我们选的点高度记作 \(f(x,y)\)，那选的点坐标即为 \((x,y,f(x,y))\)

定义：竖列 \((x,y)\) 的相邻竖列坐标可表示为 \((x-1,y)\) \((x+1,y)\) \((x,y-1)\) \((x,y+1)\)

选点坐标时有一个限制：每一个竖列选的坐标 \((x,y)\) 与其相邻的竖列 \((a,b)\) 坐标高度差不超过 \(D\)

即 \(|f(x,y)-f(a,b)|\le D\)

现在求 \(\min\sum v[x][y][f(x,y)]\)

思路：

先去掉高度差不超过 \(D\) 的条件，那么这就变成了一个求最小割的题目

我们直接把每一个竖列的所有点依次相连，容量为 \(v\) ，且从 \(s\) 连一条到这列起点，容量为 \(inf\) 的边，从这列终点连一条到 \(t\)，容量为 \(inf\) 的边

但是还有高度差不超过 \(D\) 的条件，所以考虑让建好的网络中即使割掉高度差超过 \(D\) 的地方也无影响

于是我们就只需要从 \((i,j,k)\) 向 \((i\pm 1,j,k-D)\) 和 \(i,j\pm 1,k-D\) 连一条容量为 \(inf\) 的边

会发现这样的话即使割掉所有不合法的边仍能从 \(s\) 走到 \(t\)

画图模拟一下就可以理解了

最后的结果就是最小割

P2805 植物大战僵尸

题意：

给定一个有向图，点有点权，选择一个子图，满足子图上如果选择了一个点就必须选择它之前的所有点。最大化点权和。

这里的之前所有点指从这个点出发，沿着反向边能跑到的所有点

思路：

这个题无非就是这个的变式，是一个最大权闭合子图问题

但是这道题需要除去环，所以用拓扑排序

若是拓扑排序的队列为空但某个点入度仍大于 \(0\)，则此点在一个环内，应该除去

而且这道题边是反的，因此跑完拓扑排序后把边反过来，跑一边网络流就行

具体做法不再叙述

费用流

P1251 餐巾计划问题

题意：

一个餐厅在相继的 \(N\) 天里,每天需用的餐巾数不尽相同。

假设第 \(i\) 天需要 \(r_i\)块餐巾( \(i=1\sim N\))。餐厅可以购买新的餐巾,每块餐巾的费用为 \(p\) 分;或者把旧餐巾送到快洗部,洗一块需 \(m\) 天,其费用为 \(f\) 分，或者送到慢洗部，洗一块需 \(n\) 天(\(n>m\))，其费用为 \(s\) 分(\(s<f\))。

每天结束时,餐厅必须决定将多少块脏的餐巾送到快洗部,多少块餐巾送到慢洗部,以及多少块保存起来延期送洗。但是每天洗好的餐巾和购买的新餐巾数之和,要满足当天的需求量。

试设计一个算法为餐厅合理地安排好 \(N\) 天中餐巾使用计划,使总的花费最小。

思路：

每一天要处理两件事：准备干净餐巾以及处理脏餐巾

因此考虑把每个点拆成两个：早上和晚上，早上准备干净餐巾，晚上处理脏餐巾

建立一个源点 \(s\) 和一个汇点 \(t\)

这样就做完了

P2153 晨跑

题意：

有 \(n\) 个点，\(m\) 条边，起点为 \(1\)，终点为 \(n\)，每个边都有边权

求 \(1\sim n\) 最长有几条的路线(满足每次经过的点都不相同)，且在这个情况下最少需要跑的路程是多少

思路：

这不是最小费用最大流吗？

把原路线容量设为 \(1\) ，费用设为边权就可以求解

但是要满足每次经过的点都不相同

考虑拆点

把点 \(i\) 拆成 \(i\) 和 \(i+n\)，从 \(i\) 向 \(i+n\) 连一条容量为 \(1\) 费用为 \(0\) 的边

这样就行了

答案分别是最大流和最小费用

P2469 星际竞速

题意：

给一张 DAG，边有边权

你最开始不在图内

你可以耗费 \(a_i\) 的代价直接到达 \(i\) 点，也可以消耗 \(edge_{x\rightarrow y}\) 的代价从 \(x\) 走到 \(y\)

求使所有点都被走到的最小代价

思路：

我们可以换一种理解方式：

每次都不在图内，然后瞬移到某一点 \(x\) ，然后再走

考虑费用流，让你在最大流的时候把每个点都遍历一遍，然后同时求出最小代价

从 \(s\) 点开始表示出发，走到 \(t\) 点表示结束

因此我们可以把所有边容量设为 \(1\)，这样无论如何最大流的结果都不会变

若是你想在 \(x\) 点结束，你必定是位移到 \(x\) 或从某处走到 \(x\)

考虑拆点

我们把 \(i\) 点 拆成 \(i\) 和 \(i'\) ，然后从 \(s\) 向 \(i'\) 连费用为 \(a_i\) 的边，\(i'\) 向 \(t\) 连费用为 \(0\) 的边，\(s\) 向 \(i\) 连费用为 \(0\) 的边

若存在边 \(edge(i,j)\) \(i<j\)，则从 \(i\) 向 \(j'\) 连费用为 \(edge(i,j)\) 的边

这样的话对于每一个点 \(i\) 对应的 \(i'\) 都会走向 \(t\) ，并且必定会由 \(s\) 或前面的点走到，可以更新最小答案

所以这种做法正确，最小费用即为答案

标签：费用,容量,石柱,练习,餐巾,网络,蜥蜴,inf
来源： https://www.cnblogs.com/into-qwq/p/16455752.html