7.6 圆方树
作者:互联网
\(\large \text{Date: 7.6}\)
圆方树 \(\rm Notes\)
众所周知,在无向图中,存在若干的点双联通图。
点双联通图:图中任意两不同点之间都有至少两条点不重复的路径。
我们称这张图中所有原来的点叫“圆点”。接着,对于每一个原图中的点双联通子图,我们新开一个点,删去子图中原来的边,将这个点和原来的双联通子图里的点分别连接插入另一个新的图。我们构造出来的这个点称作“方点”。可以证明这个新构建的图一定是一棵树(或森林)。
这样的一棵树就叫“圆方树”。其中圆点连接方点(圆点仍然可以对应到原图中),原图的每一个点双联通子图加上方点构成一个菊花图。
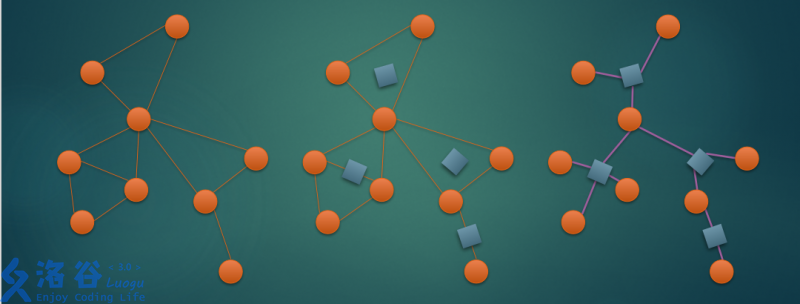
可以发现,将方点连起来的点一定是原图的割点,出度 \(>1\),其他剩下的圆点(非割点)出度均为 \(1\)。也就是说,割点同时属于多个点双联通子图,而非割点只属于一个点双联通子图。
而一个无向图的所有点双联通图可以通过\(\rm tarjan\) 轻松求得:
(这里low[u]的定义和原来 \(\rm tarjan\) 略有不同。这里 low[u] 定义为节点 \(u\) 的 DFS 树中的子树中的某个点 \(v\) 通过最多一次返祖边或向父亲的树边能访问到的点的最小 \(DFS\) 序。(所以有一个特殊的判断)
void tarjan(int u) {
low[u] = dfn[u] = ++Ti;
st[++topx] = u;
for(auto v : G[u]) { // tarjan ing
if(!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
if(low[v] == dfn[u]) {
++cnt; // cnt 的值一开始就是 n,而圆点在建图时使用原来的编号,这样所有编号 > n 的点都是方点,便于判断。
for(int x = 0; x != v; --topx) {
x = st[topx];
T[cnt].push_back(x); // build the new Graph
T[x].push_back(cnt);
}
T[cnt].push_back(u); // 此时 u 一定是割点,不能退栈
T[u].push_back(cnt);
}
}
else low[u] = min(low[u], dfn[v]);
}
}
当 \(low[v]=dfn[u]\) 时,说明节点 \(v\) 及它的子树内的节点通过最多一次返祖边或向父亲的树边能访问到的点 仅仅为 \(u\),此时栈中 \(u\) ~ \(st[top]\) 的节点构成点双联通图。我们构建出方点,在新的图中连边即可。
圆方树的妙处在于,能够新建一些“方点”,使他们能够在维护信息的时候“某种程度上”代表整个点双联通子图,从而使得维护信息更加方便。
建树代码:
#include <cstdio>
#include <vector>
#include <algorithm>
const int MN = 100005;
int N, M, cnt;
std::vector<int> G[MN], T[MN * 2];
int dfn[MN], low[MN], dfc;
int stk[MN], tp;
void Tarjan(int u) {
printf(" Enter : #%d\n", u);
low[u] = dfn[u] = ++dfc; // low 初始化为当前节点 dfn
stk[++tp] = u; // 加入栈中
for (auto v : G[u]) { // 遍历 u 的相邻节点
if (!dfn[v]) { // 如果未访问过
Tarjan(v); // 递归
low[u] = std::min(low[u], low[v]); // 未访问的和 low 取 min
if (low[v] == dfn[u]) { // 标志着找到一个以 u 为根的点双连通分量
++cnt; // 增加方点个数
printf(" Found a New BCC #%d.\n", cnt - N);
// 将点双中除了 u 的点退栈,并在圆方树中连边
for (int x = 0; x != v; --tp) {
x = stk[tp];
T[cnt].push_back(x);
T[x].push_back(cnt);
printf(" BCC #%d has vertex #%d\n", cnt - N, x);
}
// 注意 u 自身也要连边(但不退栈)
T[cnt].push_back(u);
T[u].push_back(cnt);
printf(" BCC #%d has vertex #%d\n", cnt - N, u);
}
}
else low[u] = std::min(low[u], dfn[v]); // 已访问的和 dfn 取 min
}
printf(" Exit : #%d : low = %d\n", u, low[u]);
printf(" Stack:\n ");
for (int i = 1; i <= tp; ++i) printf("%d, ", stk[i]);
puts("");
}
int main() {
scanf("%d%d", &N, &M);
cnt = N; // 点双 / 方点标号从 N 开始
for (int i = 1; i <= M; ++i) {
int u, v;
scanf("%d%d", &u, &v);
G[u].push_back(v); // 加双向边
G[v].push_back(u);
}
// 处理非连通图
for (int u = 1; u <= N; ++u)
if (!dfn[u]) Tarjan(u), --tp;
// 注意到退出 Tarjan 时栈中还有一个元素即根,将其退栈
return 0;
}
样例:
13 15
1 2
2 3
1 3
3 4
3 5
4 5
5 6
4 6
3 7
3 8
7 8
7 9
10 11
11 10
11 12
图示:

说了这么多,来看个题:
\(\text{CF 487E - Tourist}\)
题意:给定一张简单无向连通图,要求支持两种操作:
-
修改一个点的点权。
-
询问两点之间所有简单路径上点权的最小值。
不难发现,“两点之间所有简单路径”的点集就是两点之间路径所经过的所有双联通子图(割点除外)里的点的集合并。如果一条简单路径经过了一个非割点,那么这个点所属的点双联通子图中的所有点都能对答案产生贡献。这样,我们建立圆方树,将方点的权值定义为相邻圆点权值的最小值,问题转化为求书上路径最小值。
这样的话,查询套树剖 + 线段树板子即可,而修改呢?考虑暴力,一次修改一个圆点的点权,需要修改所有和它相邻的方点,这样很容易被卡到 \(O(n)\)。
这时我们可以利用圆方树是 树 的性质,将方点权值改为自己儿子圆点的权值最小值,这样修改只用修改父亲方点。对每一个方点开一个 multiset 维护权值即可。
注意查询时若 \(LCA\) 是方点,就还需要查它父亲圆点的权值。
注意圆方树的点数数组要开两倍空间。
\(\rm Code:\)
#include <bits/stdc++.h>
using namespace std;
const int N = 5e5 + 5, M = 3e5 + 5, inf = 0x7f7f7f7f;
int n, m, Q, cnt, w[N << 1];
vector <int> G[N], T[N << 1];
multiset <int> S[N << 1];
int dfn[N << 1], low[N], Ti;
int st[N], topx;
void tarjan(int u) {
low[u] = dfn[u] = ++Ti;
st[++topx] = u;
for(auto v : G[u]) {
if(!dfn[v]) {
tarjan(v);
low[u] = min(low[u], low[v]);
if(low[v] == dfn[u]) {
++cnt;
for(int x = 0; x != v; --topx) {
x = st[topx];
T[cnt].push_back(x);
T[x].push_back(cnt);
}
T[cnt].push_back(u);
T[u].push_back(cnt);
}
}
else low[u] = min(low[u], dfn[v]);
}
}
int idf[N << 1], faz[N << 1], siz[N << 1], dep[N << 1], son[N << 1], top[N << 1];
namespace TreeLink_Subdivision {
void dfsi(int u, int fz) {
faz[u] = fz; dep[u] = dep[fz] + 1; siz[u] = 1;
for(auto v : T[u]) {
if(v == fz) continue;
dfsi(v, u);
siz[u] += siz[v];
if(siz[son[u]] < siz[v]) son[u] = v;
}
}
void dfsj(int u, int fz, int Top) {
dfn[u] = ++Ti, idf[Ti] = u, top[u] = Top;
if(son[u]) dfsj(son[u], u, Top);
for(auto v : T[u]) if(v != fz && v != son[u]) dfsj(v, u, v);
}
}using namespace TreeLink_Subdivision;
namespace RE_tree {
#define lsp i << 1
#define rsp i << 1 | 1
#define mid (l + r >> 1)
#define lx lsp, l, r
#define rx rsp, l, r
int dat[N << 1];
void build(int i, int l, int r) {
if(l == r) { dat[i] = w[idf[l]]; return; }
build(lsp, l, mid); build(rsp, mid + 1, r);
dat[i] = min(dat[lsp], dat[rsp]);
}
void modify(int i, int l, int r, int p, int x) {
if(l == r) { dat[i] = x; return; }
if(p <= mid) modify(lsp, l, mid, p, x);
else modify(rsp, mid + 1, r, p, x);
dat[i] = min(dat[lsp], dat[rsp]);
}
int query(int i, int l, int r, int a, int b) {
if(r < a || b < l) return inf;
if(a <= l && r <= b) return dat[i];
return min(query(lsp, l, mid, a, b), query(rsp, mid + 1, r, a, b));
}
}using namespace RE_tree;
signed main() {
#ifndef ONLINE_JUDGE
freopen("in.txt", "r", stdin);
freopen("Ans.txt", "w", stdout);
#endif
scanf("%d %d %d", &n, &m, &Q);
for(int i = 1; i <= n; i++) {
scanf("%d", &w[i]);
}
cnt = n;
for(int i = 1; i <= m; i++) {
int u, v;
scanf("%d %d", &u, &v);
G[u].push_back(v);
G[v].push_back(u);
}
tarjan(1); dfsi(1, 0); Ti = 0; dfsj(1, 0, 1);
for(int i = 1; i <= n; i++) {
if(faz[i]) S[faz[i]].insert(w[i]);
}
for(int i = n + 1; i <= cnt; i++) {
w[i] = *S[i].begin();
}
build(1, 1, cnt);
for(int q = 1; q <= Q; q++) {
char op[3]; int x, y;
scanf("%s %d %d", op, &x, &y);
if(*op == 'C') {
modify(1, 1, cnt, dfn[x], y);
if(faz[x]) {
int u = faz[x];
S[u].erase(S[u].lower_bound(w[x]));
S[u].insert(y);
if(w[u] != *S[u].begin()) {
w[u] = *S[u].begin();
modify(1, 1, cnt, dfn[u], w[u]);
}
}
w[x] = y;
}
else {
int ans = inf;
while(top[x] != top[y]) {
if(dep[top[x]] < dep[top[y]]) swap(x, y);
ans = min(ans, query(1, 1, cnt, dfn[top[x]], dfn[x]));
x = faz[top[x]];
}
if(dfn[x] > dfn[y]) swap(x, y);
ans = min(ans, query(1, 1, cnt, dfn[x], dfn[y]));
if(x > n) ans = min(ans, w[faz[x]]);
printf("%d\n", ans);
}
}
return 0;
}
标签:cnt,联通,int,方点,dfn,7.6,low,圆方树 来源: https://www.cnblogs.com/Doge297778/p/16451319.html